|
Die absolute Wahrscheinlichkeit, eine
bestimmte Zahl zu würfeln |
 |
Wir betrachten die Wahrscheinlichkeit WN(x), mit N Würfeln,
die alle binär sind, d. h. nur Zahl oder Wappen, rot oder grün,
oder wie wir es hier verwenden, die Zahl +1 oder –1 als Augenzahl haben können. Nach einem Wurf
addieren wir (vorzeichenrichtig) und bekommen als Ergebnis eine Zahl x die zwischen –N und +N
liegen muss. Die Definition dieser Wahrscheinlichkeit ist |
| |
| WN(x) | = |
Zahl der Möglichkeiten x zu würfeln
Zahl aller
Möglichkeiten in einem Wurf | = |
Px
PN |
|
|
 |
Wie groß ist Px und PN? |
|
 |
PN, die Anzahl aller Möglichkeiten
des Ausgangs des Würfelns, ist leicht zu konstruieren:
Mit N = 1 gibt es 2 Möglichkeiten (+1
und –1); PN = 2
Mit N = 2 gibt es 4 Möglichkeiten (+1/+1 und
+1/–1 und –1/+1 und –1/+1); PN = 4
Mit N = 3 gibt es
8 Möglichkeiten (+1/+1/+1 und +1/+1/-1 und ....); PN = 8. |
|
 |
Eine Tabelle der Möglichkeiten zeigt dies graphisch; die gelben Spalten in den einzelnen
Tabellen zeigen die möglich Ergebnisse x |
|
|
| N = Zahl der Würfel |
Mögliche Würfe
und Summe (gelb) |
PN = Zahl der möglichen Würfe |
| 1 |
| 2 | | 2 |
| +1/+1 | +2 | -1/+1 |
0 | | +1/-1 |
0 | -1/-1 |
-2 |
| 4 | | 3 |
| +1/+1/+1 | +3 | -1/+1/+1 |
+1 | | +1/+1/-1 |
+1 | -1/+1/-1 |
-1 | | +1/-1/+1 |
+1 | -1/-1/+1 |
-1 | | +1/-1/-1 |
-1 | -1/-1/-1 |
-3 |
| 8 | | 4 |
| +1/+1/+1/+1 | +4 |
-1/+1/+1/+1 | +2 |
| +1/+1/+1/-1 | +2 | -1/+1/+1/-1 |
0 | | ... |
... | ... |
... | | +1/-1/-1/+1 |
0 | -1/-1/-1/+1 |
-2 | | +1/-1/-1/-1 |
-2 | -1/-1/-1/-1 |
-4 |
| 16 |
|
|
 |
Das Bildungsgesetz ist klar: |
| |
|
|
 |
Dabei haben wir aber unausgesprochen eine sehr wichtige
Annahme gemacht: .
|
|
|
Die Würfel sind unterscheidbar!
|
|
|
 |
In den obigen Tabellen ist die erste Zahl immer der 1.
Würfel, die 2. Zahl immer der 2. Würfel usw., d.h. die Würfel
tragen fiktive Nummern oder Farben als Unterscheidungsmerkmal. In anderen Worten: wir können für ein-und-dasselbe
Ergebnis unterscheiden auf wie viel verschiedene Arten wir es bekommen können.
Falls wir "Würfel"
mit mehr als 2 "Augen" betrachten, bekommen wir, leicht einzusehen, für den allgemeinen Fall eines
Würfels mit A Augen die nachfolgende Formel. Wer's nicht leicht einsieht betätigt diesen
Link. |
| |
|
 |
Es bleibt, Px (= Zahl der Möglichkeiten x zu würfeln)
zu bestimmen. Auch das läßt sich durch nachdenken und probieren ermitteln; allerdings müssen wir mehr Aufwand
treiben und sehr sorgfältig überlegen, was genau ermittelt werden soll.
|
|
 |
Betrachten wir dazu ein Beispiel. Wir haben 10 unterscheidbare digitale Würfel (N = 10), und fragen nach der Zahl der
Möglichkeiten, für die Summe
x eine +2, eine +3
oder eine –8 zu würfeln. |
|
 |
Wie auch immer die Würfel fallen, es werden N+ Würfel die +1
zeigen und N– Würfel die –1. Für unser Beispiel gelten die Gleichungen |
| |
| | Summe x = +2 |
Summe x = +3 |
Summe x = –8 |
| |
N+ + N– = 10
N+ – N– = 2
oder
2 + N– + N– = 10
N– = 4
N+ = 6 |
N+ + N– = 10
N+ – N– = 3
oder
3 + N– + N– = 10
N– = 7/3
????
|
N+ + N– = 10
N+ – N– = –8
oder
N– – 8 + N– = 10
N– = 9
N+ = 1 |
|
|
| |
|
 |
Erste wichtige Erkenntnis: Es gibt keine
Möglichkeit, eine 3 oder verallgemeinert, eine ungerade ganze Zahl zu würfeln,
da die allgemeien Gleichung N– = (10 – x)/2 für ungerade x keine ganzzahligen
Werte für N hergibt. |
|
 |
Man kann das auch anders ausdrücken, indem man die gesamte Augenzahl x
über die Zahl der N+ oder N– Würfe koppelt, es gilt |
| |
| x | = N+ – (N – N+) = |
2N+ – N |
|
|
|
 |
Dabei sind aber immer nur ganzzahlige Werte für die
N und x zugelassen! |
 |
Wir können Px damit auch über PN+,
die Zahl der Möglichkeiten N+ mal eine +1 zu würfeln, berechnen. Das ist einfacher. Px
würden wir dann erhalten, indem wir in der abzuleitenden Formel N+ durch 1/2 · (x + N) ersetzen.
|
 |
Dabei haben wir aber ein mögliches Problem
- hier liegt ein erster großer Fallstrick der Kombinatorik. Denn bei geradzahliger Würfelanzahl N
können wir nur geradzahlige Augenzahlen x erzielen, und bei ungeradzahliger Würfelanzahl
N werden wir ungerade x haben. |
|
 |
Da wir aber eine Formel suchen, die für alle
N gilt, wir aber für jedes gegebene N immer nur die Hälfte der
insgesamt vorhandenen Möglichkeiten sehen, müssen wir bei der Berechnung von Px später
etwas vorsichtig sein. |
 |
Aber nun zu Px oder PN+. Natürlich ist
die Formel dazu bekannt, wir wollen sie hier aber ausführlich
ableiten.
Um Bildungsgesetze in der Kombinatorik zu erkennen oder zu überprüfen, empfiehlt es sich zunächst
immer, eine Tabelle zu machen. Bleiben wir also bei N = 10 Würfeln und betrachten die erzielbaren Ergebnisse
für die 10 Möglichkeiten für N+. Dabei bedenken wir, daß die Würfel unterscheidbar sind. Man kann das so ausdrücken: |
|
 |
Würfeln wir mit 10 roten, grünen, blauen, .... Würfel,
sind auch die Kombinationen
-1, +1, +1, ....
+1, -1, +1. ....
usw.
alle unterscheidbar - obwohl das Ergebnis immer +9 ist. |
|
 |
Hier versteckt sich schon die nächst wichtige Lehre: Wir müssen nicht nur aufpassen,
ob die Würfel unterscheidbar oder ununterscheidbar sind, sondern diese Frage auch
auf Kombinationen anwenden. Selbst wenn die obigen Würfel alle rot und damit ununterscheibar
wären, könnten wir dennoch evtl. die Kombiuationen noch unterscheiden. Wir
werden das gleich näher kennenlernen. |
 |
Jetzt noch schnell ein weiterer Punkt. Falls wir mit einem
Würfel 10 mal würfeln, statt mit 10 Würfeln 1 mal, erwarten wir - statistisch - dasselbe
Ergebnis. Das ist die "Zeitmittel = Scharmittel" Hypothese,
die uns schon früher begegnet ist. Das scheint zwar selbstverständlich zu sein, aber bei genauem Hinsehen kann
es hier durchaus Probleme geben. |
|
 |
Falls wir mit einem Würfel 3 mal hintereinander
würfeln würden, drückt sich die jetzt sinnlose Unterscheidbarkeit des Würfels in der Unterscheidbarkeit
des Wegs zum Ziel aus: Die Sequenz +1, +1, -1 ist ein anderer Weg zum Endpunkt +2 als die Sequenz
–1, +1, +1. |
 |
Hier ist die entsprechende Tabelle |
| | |
| N+ | N– |
S |
Zahl Möglichkeiten | Kommentar |
Formel
PN+ = | | 0 | 10 | -10 |
1
| Würfelnummer |
| 1 | 2 |
3 | 4 |
5 | 6 |
7 | 8 |
9 | 10 |
| -1 | -1 | -1 | -1 |
-1 | -1 | -1 | -1 |
-1 | -1 |
|
| ? | | 1 | 9 |
-8 | 10
| Würfelnummer |
| 1 | 2 |
3 | 4 |
5 | 6 |
7 | 8 |
9 | 10 |
| +1 | -1 | -1 | -1 |
-1 | -1 | -1 | -1 |
-1 | -1 | | -1 |
+1 | -1 | -1 | -1 |
-1 | -1 | -1 | -1 |
-1 | | 10 Zeilen...... |
| -1 | -1 | -1 |
-1 | -1 | -1 |
-1 | -1 | -1 |
+1 |
|
Nicht nur die Würfel, auch alle ihre Anordnungen
sind unterscheidbar.
Dies bedeutet: Wenn man einen bestimmten Würfel auf +1
setzt und dann die Möglichkeiten für die anderen Würfel "durchdekliniert", wird keine der auftretenden
Kombinationen identisch sein mit den Kombinationen, die man erhält wenn man diese "Deklinationsübungen"
mit einem anderen auf +1 gesetzten Würfel durchführt. |
N (?) | | 2 | 8 | -6 |
45
Wir bräuchten jetzt eine dreidimensionale Tabelle - ersatzweise machen wir
mehrere Tabellen
1. Tabelle:
1. Würfel immer +1
| Würfelnummer |
| 1 | 2 |
3 | 4 |
5 | 6 |
7 | 8 |
9 | 10 |
| +1 | +1 |
-1 | -1 | -1 |
-1 | -1 | -1 | -1 |
-1 | | +1 |
-1 | +1 | -1 | -1 |
-1 | -1 | -1 | -1 |
-1 | | 9 Zeilen...... |
| +1 | -1 | -1 |
-1 | -1 | -1 | -1 |
-1 | -1 | +1 |
2. Tabelle: 2. Würfel immer +1
| Würfelnummer |
| 1 | 2 |
3 | 4 |
5 | 6 |
7 | 8 |
9 | 10 |
| +1 | +1 |
-1 | -1 | -1 |
-1 | -1 | -1 | -1 |
-1 | | -1 |
+1 | +1 | -1 |
-1 | -1 | -1 | -1 |
-1 | -1 | | 9 Zeilen...... |
| -1 | +1 |
-1 | -1 | -1 | -1 |
-1 | -1 | -1 | +1 |
3. Tabelle: 3. Würfel +1; 9 Möglichkeiten für den Rest.
.....
Und so weiter - Insgesamt 10 Tabellen |
Es gibt 9 Möglichkeiten falls der 1. Würfel +1 zeigt.
Es gibt 9 Möglichkeiten
falls der 2 Würfel +1 zeigt.
usw.; das Ganze N mal.
Aber: Es gibt trotz unterscheidbarer Würfel
jetzt ununterscheidbare Anordnungen:
Ob der m-te Würfel
auf +1 gesetzt ist und der k-te Würfel bei der "Durchdeklination" +1 zeigt ist ununterscheidbar von der Anordnung, in der der k-te Würfel auf +1 gesetzt
ist und der m-te Würfel beim "Durchdeklinieren" +1 zeigt.
Bei allen Kombinationen gibt
es zwei dieser ununterscheidbaren Annordnungen.
In den beiden ausgeführten Tabellen sind sie rosa markiert! Nur die Hälfte
aller Möglichkeiten darf also berücksichtigt werden - wir müssen durch 2
dividieren. Insgesamt erhalten wir (9 · 10)/2 = 45 Möglichkeiten eine 8 zu würfeln. |
(N · (N - 1))/2 (?) | | 3 | 7 |
-4 | 120
Siehe nebenstehenden Text |
Wir setzen einen 1. Würfel auf +1: Dann haben wir (N - 1) Möglichkeiten
für einen weiteren Würfel mit +1 und (N - 2) Möglichkeiten für den letzten Würfel,
der +1 zeigen muß.
Insgesamt gibt es N(N - 1)(N - 2) Möglichkeiten der "Durchdeklination"
Darunter sind aber jeweils 6
ununterscheidbare Anordnungen. Dies wird klar, wenn wir beispielsweise die Anordnungsmatrix
betrachten, bei der die Würfel Nr.1, Nr.4 und Nr.8 die +1 zeigen. Alle diese Anordnungen sind ununterscheidbar!
Die Farbcodierung bedeutet:
rot = primär "gesetzt"
blau = sekundär gesetzt
grün = verbeibende Möglichkeit
| + | - | - | + |
- | - | - | + | - | - |
| + | - | - | + | - |
- | - | + | - | - |
| + | - | - | + | - |
- | - | + | - | - |
| + | - | - | + | - |
- | - | + | - | - |
| + | - | - | + | - |
- | - | + | - | - |
| + | - | - | + | - |
- | - | + | - | - |
| (N(N - 1)(N - 2))/1· 2 · 3 (?) |
| Allgemein | | x | 10 - x |
-10
...
+10 | ... |
(Zahl der möglichen "Deklinationen")/(Zahl der ununterscheidbaren Anordnungen)
Das Bildungsgesetz ist offenbar
| PN+ = |
N · (N – 1) · (N - 2) · ... · (N – N+ + 1)
1 ·
2 · 3 · ... · N+ |
|
|
| |
 |
Das ist dieselbe Formel wie bei der Zahl
der Anordnungen von Leerstellen. Bevor wir die obige Formel weiterentwickeln, aber noch einige Anmerkungen zu den Fallstricken der Kombinatorik. |
|
 |
Man muß sorgfältig trennen zwischen unterscheidbaren oder ununterscheidbaren Würfeln (oder Teilchen)
und Anordnungen. Die Würfel
in obiger Tabelle sind unterscheidbar (durch ihre Nummer bzw. Spalte in der Tabelle),
einige ihrer Anordnungen in der obigen Systematik aber nicht.
Man müßte ein zweites Merkmal einführen (in der Tabelle ist das die
Farbe für die Nummer der "Setzung"), um auch alle Anordnungen unterscheiden zu können. |
|
 |
Die unterscheidbaren Anordnungen sind oft leichter zu sehen, wenn man nicht mit
N Würfeln gleichzeitig wirft, sondern mit einem Würfel N mal
- das Ergebnis wird dasselbe sein, aber man wird identische Anordnungen nicht doppelt
zählen. Dies ist am einfachsten in einer Graphik
darstellbar. |
 |
Die Sprache ist manchmal zu begrenzt, um die Feinheiten eindeutig darzustellen
oder gibt Anlaß zu Mißverständnissen. Betrachten wir einen Satz aus obiger Tabelle:
|
|
 |
Wir setzen einen 1. Würfel auf +1:
Dann haben wir (N - 1) Möglichkeiten für einen weiteren Würfel mit +1 und (N - 2) Möglichkeiten
für den letzten Würfel, der +1 zeigen muß. |
|
 |
Man hätte auch schreiben können:
Wir setzen die
1. Münze auf +1: Dann haben wir (N - 1) Möglichkeiten für die
2. Münze mit +1 und (N - 2) Möglichkeiten für die 3.
Münze die +1 zeigen muß. |
|
 |
Oder vielleicht:
Wir setzen den 1. Würfel
auf +1: Dann haben wir (N - 1) Möglichkeiten für den
2. Würfel mit +1 und (N - 2) Möglichkeiten für den 3.
Würfel, der +1 zeigen muß. |
|
 |
Das wäre nicht falsch gewesen, aber möglicherweise mißdeutig.
Denn mit den Bezeichnungen 1., 2. und 3. Würfel meinen wir in diesem Zusammenhang nicht die Würfel
mit den Nummern
1, 2 und 3 (das Unterscheidungsmerkmal der Würfel), sondern die Reihenfolge,
in der wir die Werte "setzen". |
 |
Das größte Problem ist vielleicht, daß normale Menschen kein
Gefühl für das ungefähre Ergebnis einer kombinatorischen Aufgabe haben. Wieviele fünfstellige Zahlen
kann man mit den Ziffern 0, 3, 5, 9 bilden? Wenn die 0 nicht am Anfang stehen darf? Wenn keine Ziffer mehr
als 2 mal vorkommen darf? Wenn jede Ziffer mindesten 1 mal vorkommen muß? |
|
 |
Wenige Menschen werden bei dieser simplen Aufgabe ein Gefühle für die Größenordnung
der Antwort und die Reihenfolge der Lösungen geordnet nach Größe haben - es hilft nichts, man muß
rechnen. |
 |
Jetzt aber zu unserer Formel für PN+. Wie bei der Berechnung
der Leerstellenkonzentration, erweitern wir erst mit (N - x)! um eine besserer Darstellung zu bekommen. Die Ausgangsformel
ist |
| |
| P+ | = |
N(N – 1)(N – 2) · .. · (N – N+ + 1)
1 ·
2 · 3 · ... · N+ | = |
N(N – 1)(N – 2) · ... · (N – N+ + 1)
N+! |
|
|
|
 |
Multiplizieren mit (N - N+)!/(N - N+)! ergibt N!
im Zähler und N+! · (N - N+)! im Nenner, wir erhalten |
| |
| PN+ | = |
N!
N+! · (N – N+)! | = |
æ
è | N
N+ |
ö
ø |
|
|
 |
Diese Formel hat einen eigenen Namen: Es ist der Binominalkoeffizient von N und N+; geschrieben in Klammern
ohne Bruchstrich wie oben gezeigt. |
|
 |
Der Binominalkoeffizient ist die Lösung einer Standardaufgabe der Kombinatorik,
die in verschiedenster Gestalt immer wieder vorkommt: Wieviele Möglichkeiten gibt es, aus
N Elementen N+ auszuwählen, wobei wir zwar die Elemente, nicht aber die Anordnungen unterscheiden.
|
 |
In unserer ursprünglichen Fragestellung wollten wir aber nicht N+
ausrechnen, d.h. die Zahl der Möglichkeiten, daß N+ von N Würfeln +1 zeigen
(oder nach N mal würfeln mit einem Würfel N+ mal die +1 kam) , sondern P(x),
die Zahl der Möglichkeiten die Zahl x zu würfeln. Wie weiter oben schon
festgehalten, müssen wir dazu N+ durch 1/2 · (x + N) substitutionieren. Wir erhalten
dann für Px |
|
|
| |
|
| |
| Px | = |
N!
{1/2 · (x + N)}! · {N – [1/2 · (x + N)]}! |
| | | | | = |
N!
{1/2 · (N + x)}! · {1/2 · (N – x)}! |
|
|
 |
Damit können wir unsere ursprüngliche Fragestellung
beantworten. Wie groß ist die Wahrscheinlichkeit WN(x), mit N Würfeln, die alle digital
sind, d. h. nur +1 oder -1 als Augenzahl haben, mit einem Wurf eine Summe x zwischen -N und
+N zu würfeln. Die Definition dieser Wahrscheinlichkeit war |
|
 |
WN(x) = (Zahl der Möglichkeiten x zu würfeln)/(Zahl aller Möglichkeiten in einem
Wurf) = Px/PN. Somit ergibt sich mit den jetzt bekannten Formeln für Px
und PN = 2N |
| |
| WN(x) = |
N!
2N · {1/2 · (N + x)}! · {1/2
· (N - x)}! |
|
|
 |
Diese Formel ist noch exakt richtig. |
|
 |
Sie gibt jedoch nur sinnvolle Antworten,
falls N und x
beide geradzahlig, oder
beide ungeradzahlig sind. |
|
 |
Das ist leicht zu sehen: Setzen wir z.B. N = 8 und x = 3, bekommen wir im Nenner
die Ausdrücke 5,5! und 2,5! - und das gibt es nicht (zumindest nicht in der Kombinatorik).
|
 |
In anderen Worten: Unsere obige Formel deckt nur die
Hälfte aller Möglichkeiten ab, die wir im allgemeinen Fall haben werden. Bei der jetzt erfolgenden
Verallgemeinerung müssen wie deshalb schreiben: |
|
|
| WN(x) = 0,5 ·
|
N!
2N · {1/2 · (N + x)}! · {1/2
· (N - x)}! |
|
|
| | |
|
| |
Die genäherte Wahrscheinlichkeitsdichte |
 |
Da man mit Fakultäten nicht allzuviel anfangen kann, wird jetzt mit Hilfe
der Stirlingsche Formel
mathematisch genähert. Aus Gründen, die wir später noch genauer diskutieren,
verwenden wir hier aber die "bessere" Version der Stirlingschen Formel, nämlich den Ausdruck |
|
 |
Stirlingsche Formel: |
| |
| ln N! » (N + 1/2) · ln N – N + ln (2p)1/2
|
|
|
 |
Es bleibt noch die reine Rechenaufgabe, aus WN(x) mit Hilfe
der obigen Stirlingschen Formel und evtl. weiteren sinnvoller Näherungen eine passende analytische
Gleichung zu machen. Da der Umgang mit der Stirlingschen Formel geübt sein will, wollen wir das in einer Übungsaufgabe
tun. |
|
 |
Dabei gibt es noch einige weitere Überraschungen mathematischer Art; es lohnt sich unbedingt
hier zu üben oder zumindest die Lösung der Aufgabe anzuschauen. |
|
|
| |
| Übung
6-5 |
| Umgang mit Fakultäten und der Stirlingformel |
|
| |
 |
Die obige Formel oder Gauss Verteilung gibt jetzt auch sinnvolle
Antworten auf Fragen, die unsere Ausgangsformel verweigert hätte. Wir erhalten jetzt auch Zahlenwerte falls wir x
ungeradzahlig wählen und N
geradzahlig (und umgekehrt). Besteht hier ein Zusammenhang? |
|
Ja! Denn wir suchen ja eine Formel, die für alle
N gilt, bisher erhalten wir aber für jedes gegebene N immer nur die die Hälfte
der insgesamt vorhandenen Möglichkeiten aus der Menge der N. In anderen Worten: Wenn ich nicht weiß,
ob N geradzahlig oder ungeradzahlig ist, wird eine Wahrscheinlichkeit z.B eine geradzahlige Zahl x zu würfeln
nur halb so hoch sein wie für geradzahlige N errechnet, denn die Wahrscheinlichkeit für ein geradzahliges N
ist natürlich ½. |
 |
Die Gaussverteilung (wie auch unsere analytische Formel) ist keine abolute
Wahrscheinlichkeit mehr, sondern eine Wahrscheinlichkeitsdichte (das wird gleich im Detail erläutert). |
|
 |
Sie gibt uns auch einen Zahlenwert für die Wahrscheinlichkeitsdichte, die Zahl 6,5 oder auch die Zahl p zu würfeln.
Sowas gibt es nicht, und damit kann es auch keine absolute Wahrscheinlichkeit dafür
geben.
Zu absoluten Wahrscheinlichkeiten für die Fälle, die es gegen
kann, kommt man, indem man den (Mittel)wert der Gaussverteilung in dem Intervall zwischen den wirklich erreichbaren Werten
mit dem Wert des Intervalls multipliziert - und in unserem Fall wäre dieses Intervall = 2, da wir ja immer nur
von geraden zu geraden oder ungeraden zu ungeraden Zahlen "materialisieren" dürfen. |
 |
In der Ableitung der Gauss-Verteilung im "Atkins", an der sich dieser Modul ausrichtet, sind im übrigen ebenfalls Fehler
zu verzeichnen; das Endergebnis aber ist richtig. |
 |
Nach viel Mühen erhalten wir also tatsächlich als Ergebnis die berühmte
Gaußverteilung, die Normalverteilung oder
die Gaußsche Glockenkurve, benannt nach dem berühmten Mathematiker
Gauß, eine der wichtigsten Funktionen der Statistik. |
| |
| | |
Einige Eigenschaften und Besonderheiten
|
 |
Mit der Herleitung der Gaußschen Glockenkurve für ein Münzwerfspiel
haben wir unsere eigentliche Aufgabe noch nicht gelöst. Wir wollten wissen, wie
weit im Mittel bei einem "Random Walk" ein
Teilchen sich nach N Sprüngen von seinem Ausgangspunkt entfernt hat. |
|
 |
Mit der zugehörigen Gaußverteilung kennen wir erstmal die Wahrscheinlichkeit,
ein Teilchen bei eindimensionaler Diffusion nach N Schritten x Einheiten
vom Ursprung entfernt zu finden. |
|
 |
Dazu verschieben wir einfach unser Teilchen um eine Einheit nach rechts (+x) oder links
(–x) je nachdem ob wir +1 oder -1 würfeln. Oder, falls wir mit N Würfeln auf
einmal würfeln, verschieben wir es eben um den Wert x der sich ergibt. |
 |
Wir müssen nun, um zum Ziel zu kommen, erstmal die entsprechenden Wahrscheinlickeiten
für die dreidimensionale Diffusion betrachten und daraus dann die entsprechenden
Schlüsse ziehen. |
|
 |
Das kann man auf verschiedene Weisen tun. Ein Weg ist
sicherlich, die obige Betrachtung auf die normalen Würfel mit 6 Augen auszudehnen, mit einer Konvention für
die Zuordnung der Augenzahlen zu den Bewegungen, z.B. 1 = +x, 2 = –x, 3 = +y, usw.. |
|
 |
Man kann aber auch 3 Sätze von digitalen Würfeln
(= Münzen) nehmen, z.B. 1-, 2- und 5 DM Münzen (so man sie nach Einführung des Euro
noch hat), und eine Münzsorte für die Bewegung in einer
Koordinatenachse verwenden. Wiederum ist es egal, ob wir N (unterscheidbare; z.B. numerierte) Münzen jeder Münzsorte
gleichzeitig werfen oder sequentiell, d.h. erst fürdie x-Achse, dann für die y-Achse, schließlich
für die z-Achse (in dieser Vorgehensweise genügte auch schon eine Münzsorte, wir müssen aber
immer wissen für welche Achse wir werfen). |
|
 |
Die Vorgehensweise ist deswegen egal, weil die Bewegungen in den drei Achsen vollständig
unabhängig voneinander sind. Was auf der y- Achse geschieht wird in keinster Weise davon beeinflußt,
was auf den beiden anderen Achsen vor sich geht. |
 |
Das hat eine wichtige Konsequenz, die uns die Rechnung sehr erleichtert: Die Einzelwahrscheinlichkeiten
für die einzelnen Koordinaten sind alle identisch, unabhängig voneinander
und gehorchen der bereits abgeleiteten Formel. Die Gesamtwahrscheinlichkeit wN(x,y,z), das Teilchen bei
den Koordinaten (x,y,z) zu finden, ist damit das Produkt der Einzelwahrscheinlichkeiten:
|
|
 |
wN(x,y,z) = wN(x) · wN(y) · wN(z)
|
 |
Wenn man die Gauss-Verteilung einsetzt (mir Koordinaten oder
Ortsvektor r) erhält man |
| |
|
| wN(x,y,z) = |
æ
è |
1
2pN |
ö
ø |
3/2 | · exp – |
æ
è |
x2 + y2 + z2
2N |
ö
ø |
| | | |
| |
| | |
| | = |
æ
è |
1
2pN |
ö
ø |
3/2 | · exp – |
æ
è |
r2
2N |
ö
ø |
|
|
 |
Das war recht einfach und schmerzlos. Das Ergebnis zeigt Kugelsymmetrie, wie es
auch sein muß, d. h. die Wahrscheinlichkeit, das Teilchen irgendwo bei (x,y,z) zu finden, hängt nur vom
Abstand |r| = r = (x2 + y2+ z2)1/2 des Teilchens vom Ursprung
ab. Grundsätzlich aber ist r ein Vektor; das muß immer berücksichtigt werden (auch wenn wir
jetzt den Unterstrich wieder weglassen). |
 |
Haben wir damit unsere Aufgabe gelöst? Wir haben jetzt schließlich
eine Formel für die Wahrscheinlichkeit, das Teilchen bei jeder beliebigen Koordinate r = (x,y,z) zu finden.
Aber die Antwort ist trotzdem: Nein!
Unserer Formel ist mit zwei
Besonderheiten behaftet, die wir berücksichtigen müssen! |
|
 |
1. Die Gaußschen Glockenkurve ist zunächst eine Näherungsformel.
Wir haben zwei Näherungen gemacht: eine mathematische (Stirlingsche Formel)) und eine physikalische (x/N <<1). Über die damit verbundenen Konsequenzen sind wir uns halbwegs klar: Die Gaußsche
Glockenkurve ist aber für große N schon gut genug, und hier liegt nicht das Problem. |
|
 |
2. Die Gaußsche Glockenkurve hat aber eine ganz andere Qualität,
als die Ausgangsformel mit den Fakultäten! Sie ist nicht mehr diskret
wie die Ausgangsformel, sondern eine Kontinuumsformel, d.h. sie ist auch für nicht-ganzzahlige
x definiert. |
|
 |
Damit haben wir eine subtile Änderung der Bedeutung des
Begriffs Wahrscheinlichkeit durchgeführt. Wir haben einen Übergang von einer absoluten
Wahrscheinlichkeit zu einer Wahrscheinlichkeitsdichte gemacht. |
 |
Was das bedeutet, kann man sich auf mehrere Arten verdeutlichen: |
|
 |
In unserem Beispiel (und in jedem beliebigen anderen Beispiel), ist die absolute
Wahrscheinlichkeit W (zur Unterscheidung jetzt groß geschrieben) nur für diskrete
Werte von (X,Y,Z) definiert. Um diese Werte aus der kontinuierlichen Formel zu erhalten, müssen wir den Raum
in Zellen einteilen mit Zellabstand = Abstand zwischen den diskreten Werten und die Wahrscheinlichkeitsdichte in der gewünschten
Zelle aufintegrieren. Wir erhalten W(X,Y,Z) = 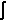 w(x,y,z)dV wobei die Integration
über die Zelle führt. Ist die Zelle so klein, daß in ihr w(x,y,z) »
const. gilt, erhalten wir direkt W(X,Y,Z) » w(x,y,z) ·V w(x,y,z)dV wobei die Integration
über die Zelle führt. Ist die Zelle so klein, daß in ihr w(x,y,z) »
const. gilt, erhalten wir direkt W(X,Y,Z) » w(x,y,z) ·V
|
|
 |
Daß man w(x,y,z) nicht mit W(X,Y,Z) verwechseln darf, ergibt sich auch rein logisch
aus der Definition einer absoluten Wahrscheinlichkeit. Denn jedes beliebige Volumen enthält ¥
viele Punkte (x,y,z), so daß die absolute Wahrscheinlickeit, eine endliche
Zahl von Teilchen oder Vorgängen bei irgendeinem von ¥ vielen Punkten zu finden
immer W(x,y,z) = 0 sein muß. w(x,y,z) ist aber nicht = 0 für beliebige Koordinaten; es kann
also nicht eine absolute Wahrscheinlichkeit ausdrücken. |
|
 |
Wir hatten exakt die gleich Situation bereits bei der Interpretation
der Wellenfunktion
y(x,y,z) kennengelernt. Auch dort war nur y(x,y,z) ·
dV, und nicht y(x,y,z) selbst ein Maß für die absolute
Wahrscheinlichkeit. |
 |
Das bringt uns auf eine Übungsaufgabe: Da die Wahrscheinlichkeit, das Teilchen
irgendwo zu finden = 1 sein muß, gilt für Wahrscheinlichkeitsdichten immer die Normierungsbedingung |
| |
+¥
ó
õ
–¥ | w(x,y,z)dxdydz = 1 |
|
|
|
 |
Da wir bei der Herleitung der Glockenkurve keine freien Parameter haben, sollte diese Bedingung eigentlich
erfüllt sein (allerdings möglicherweise nur ungefähr, da wir bei der Herleitung der Gaußverteilung
genähert haben?) Das läßt sich überprüfen - auf zur Normierung Gaußverteilung, aber bitte
mal selbst machen. |
 |
Mit der Gaußverteilung als Wahrscheinlichkeit(sdichte), das Teilchen in einem gegebenen
Volumenelement zu finden, kann man nun eine Vielzahl von Fragen stellen und lösen, jeweils noch getrent nach ein- zwei-
und dreidimensionalem "Random Walk". Wir stellen uns einigen der möglichen Fragen und illustrieren was gemeint
ist für den zweidimensionalen Fall |
|
|
 |
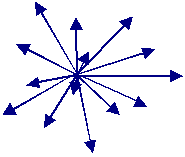
1. Was ist der Mittelwert aller möglichen Vektoren r vom Startpunkt bis zum Endpunkt nach N Sprüngen?
|
|
 |
Die Antwort darauf ist trivial: Da für jeden beliebigen Vektor r, der einen
Endpunkt charakterisiert, mit gleicher Wahrscheinlichkeit auch der Vektor –r vorkommen wird, gilt für
den Mittelwert von r - wir schreiben <r> - immer
<r> = 0. |
| |
|
 |
| Mögliche Endpunkte eines zweidimensionalen "random
walks" nach einer Zahl von N Schritten. |
Verteilung der Endpunkte der Vektoren r in der x-y-Ebene. |
|
|
 |
Diese Frage ist also bei einem echten "random walk" nicht spannend - das Ergebnis
ist immer <r> = 0. Man kann das Ganze aber auch "rückwärts" betrachten: Falls wir
<r> ¹ 0 finden - zum Beispiel als experimenteller Befund - haben wir
keinen "random walk". |
 |
2. Eine viel bessere Frage ist die nach dem Mittelwert der
Beträge von r. |
|
 |
Das läßt sich am einfachsten machen, indem wir r quadrieren und für
den Betrag |r| = r = (r2)½ schreiben. Das bedeutet, wir fragen jetzt primär
nach dem Mittelwert von (r2)½. |
|
 |
Dazu müssen wir die Wahrscheinlichkeit für das Auftreten des Wertes |r|
kennen, oder - wir behandeln den zweidimensionalen Fall - die Wahrscheinlichkeit dafür,
daß r zwischen |r| und |r| + D|r| liegt. |
 |
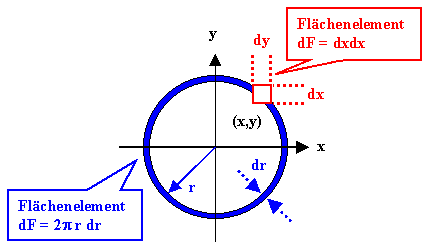
Wir fragen - und das ist sehr wichtig - jetzt nur noch
nach der Wahrscheinlichkeit für das Auftreten einer bestimmten Länge von r , eben |r|,
und nicht mehr danach in welchem (cartesischen) Flächenelement DF(x,y) = DxDy der Vektor r endet. |
| |
|
| |
 |
|
Das Flächenelement Dx·Dy
muß jetzt (im zweidimensionalen) durch die Fläche des Rings
der Breite Dr im Abstand r ersetzt werden, d.h. das Flächenelement heißt
jetzt
DF(r) = 2p·r · Dr (= Umfang
der Kreises mit Radius r mal "Höhe" - gut genug für differentiell kleine Dr).
Dies ist unten graphisch dargestellt (wobei wir D = "d") um anzudeuten daß
wir immer differentiell kleine Änderungen meinen). |
| |
|
|
 |
Dreidimensional fragen wir nur noch nach der Wahrscheinlichkeit,
daß r irgenwo in der Kugelschale zwischen |r| und |r| + D|r|
endet. Das cartesisiche Volumenelement DV(x,y,z) = DxDyDz
wird zu DV(r) = 4p·r2 · Dr. |
| |
Für die Wahrscheinlichkeit, r irgendwo zwischen r und r
+ Dr zu finden gilt entsprechend der obigen Ableitung für
den zweidimensionalen Fall |
|
|
| wN(r)·pr ·Dr = WN(r)
= | æ
è |
1
2pN |
ö
ø | 1 |
· exp – | æ
è |
x2 + y2
2N |
ö
ø |
·2pr ·Dr = |
r ·Dr
2N |
· exp – | r2
2N |
|
|
| | | |
|
 |
Wir haben ein Produkt einer ansteigenden Geraden mit einer abfallenden Exponentialfunktion |
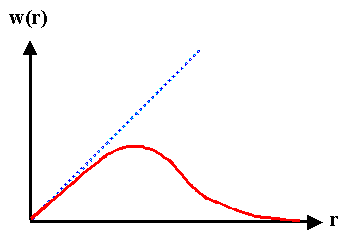
|
 |
Das sieht ungefähr so aus ®
|
 |
Wiederum ist die Verteilungskurve nur für positve Werte von r definiert, und wenn alles stimmt,
muß das Integral über die Kurve = 1 sein |
|
| | |
 |
Damit haben wir jezt die Wahrscheinlichkeitsverteilung für das Autreten gewisser Abstände
r vom Ursprung - für den ein- und zweidimensionalen Fall siehe den Link. |
|
 |
Die Formel zur Berechnung des Mittelwerts von r2
bei gegebener Verteilung w(r) lautet in der bekannten Integralformel für Mittelwerte: |
| | | |
| | |
| <r2> = |
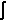 r2w(r)dr r2w(r)dr
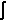 w(r)dr w(r)dr | = | +¥
ó
õ
–¥ |
r2w(r)dr |
|
|
| | | |
|
 |
Dabei ist mitgenommen, dass der Wert des Nenners per Definition = 1 sein muß. Die Integrationen
laufen selbstverständlich alle von –¥ bis +¥ |
 |
Diese Größe hat zentrale Bedeutung und deshalb einen eigenen Namen, sie heißt
"Mittleres Verschiebungsquadrat". |
|  |
Damit ist die Frage nach den Mittelwerten im Prinzip gelöst;
die entsprechenden Formeln finden sich in einer gesonderten Tabelle. |
 |
3. Wir können aber auch fragen: In welchem Abstand |r|wahr
(wieder nur Betrag bei r; wir lassen die Betragsstriche aber zukünftig weg!) ist die Wahrscheinlicheit,
das Teilchen zu finden am höchsten? Wir fragen nach dem wahrscheinlichsten
Abstand. |
|
 |
Das ist die Frage nach dem Maximum der Funktion w(r).
Die obige Figur zeigt, daß ein Maximum vorhanden ist; die Frage ist also sinvoll. |
|  |
Daß wahrscheinlichste Werte und Mittelwerte
ganz verschieden sein können, sieht man sofort ein, wenn man sich fragt, was das wahrscheinlichste
und das mittlere Gehalt einer Gruppe von 100 Personen ist, in der 95 Personen €
2.000.- pro Monat verdienen, und 5 Personen € 20.000.000.- pro Monat bekommen. |
|  |
Eine Antwort findet sich ein einem eigenen Modul und
in der großen Tabelle. |
 |
4. Wir können weiterhin fragen, bei welchem r die Wahrscheinlichkeitsverteilung
eine bestimmte Breite hat, oder andersherum, wie groß die Halbwertsbreite,
d.h. die Breite (ausgedrückt in r) in halber Höhe ist? Oder ganz allgemein, wie die Breite der verteilung
von den Parametern (hier N) abhängt. |
 |
Alle diese Fragen sind sinnvoll und haben wichtige Bedeutungen. Sie sind in weiteren Modulen
behandelt. Der wahrscheinlichste Abstand beim dreidimensionalen "Random Walk"
ist ausführlich dargestellt, die Gesamtheit der Fragen und Antworten tabellarisch. |
| |
| |
 |
Die letzte Frage ist jetzt: Wie hängen der Diffusionskoeffizient
und die oben betrachteten Größen <r2> oder rwahr zusammen? Ein Zusammenhang
muß existieren, da wir letztlich mit dem "Random Walk" und den Diffusionsgleichungen
der Fickschen Gesetze sehr ähnliche Abläufe beschreiben. |
|
 |
Um diesen Zusammenhang zu erhalten müssen wir uns nur klar machen, daß wir mit
der Herleitung der obigen Formeln für den "Random Walk" ein sehr allgemeines Diffusionsproblem gelöst
haben. Wir haben betrachtet, wie sich eine Konzentration an Teilchen, die zum Zeitpunkt t = 0
alle bei (x,y,z) = 0 zu finden waren, im Laufe der Zeit im gesamten Volumen einstellt,
d.h. wir haben eigentlich das 2 Ficksche Gesetz für die Randbedingung einer Anfangsverteilung in Form einer d-Funktion gelöst ohne es zu kennen oder vorauszusetzen.
Mit den in der tabellarische Darstellung gegebenen Funktionen kennen wir jetzt
die Konzentrationsverteilung für alle Dimensionen. |
|  |
Wir müssen jetzt nur noch das 2 Ficksche Gesetz für diese Bedingungen formal
lösen, und diese Lösung mit der hier gegebenen vergleichen. Dabei rechnen wir die Konzentration c, die
im Fickschen Gesetz auftritt, über folgende Beziehung auf die Wahrscheinlichkeiten um, die wir hier abgeleitet haben:
|
|
 |
w(r,t) = Wahrscheinlichkeit ein Teilchen zur Zeit t im Intervall r, r + dr zu finden
= Zahl der Teilchen bei (r,t)/Zahl aller Teilchen, oder |
|
|
| w(r,t) = | c(r,t)
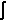 c(r,t)dr c(r,t)dr |
|
|
 |
Es genügt der eindimensionale Fall. Welcher Randbedingung entspricht unser Würfelexperiment?
Da 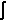 w(r) immer = 1 ist, haben wir offenbar eine bestimmte Anzahl von Teilchen, die
bei t = 0 alle bei r = 0
waren; d.h. eine durch eine d-Funktion symbolisierte Quelle im Inneren eines Körpers. w(r) immer = 1 ist, haben wir offenbar eine bestimmte Anzahl von Teilchen, die
bei t = 0 alle bei r = 0
waren; d.h. eine durch eine d-Funktion symbolisierte Quelle im Inneren eines Körpers.
|
|
 |
Die entsprechende Lösung des eindimensionalen
2. Fickschen Gesetzes geben wir sowohl mit x als Koordiante, als auch mit |r| als Koordinate an - dies ist
sehr lehrreich und hilft, die oft vorliegende Konfusion zu vermeiden. |
| |
| wN(x)dx |2.FG = |
æ
è | 1
p4D·t | ö
ø |
1/2 | · exp – |
æ
è | x2
4D·t | ö
ø |
|
| wN(r)dr |2.FG = |
æ
è | 1
pD·t | ö
ø |
1/2 | · exp – |
æ
è | r2
4D·t | ö
ø |
|
| Mit Koordinate
x |
Mit Koordinate |r| |
|
|
 |
Graphisch sieht das so aus (immer bedenken: Es gibt keine negativen
|r|; daher der Faktor 2 im eindimensionalen Volumenelement dr
|
| | |
.png) |
.png) |
| Mit Koordinate
x |
Mit Koordinate |r| |
|
| | |
| |
|
|
 |
Aus der Betrachtung des eindimensionalen "Random
Walks" erhielten wir für |r|:
|
| | |
| wN(r)dr |RW = | æ
è |
2
a02pN |
ö
ø | 1/2 | · exp – |
æ
è | r2
2Na02 | ö
ø |
|
|
|
 |
Aus einem Vergeich des Exponentens oder des Vorfaktors erhalten wir sofort:
|
| |
oder
|
| (n = Sprungrate
= N/t) |
|
|
 |
Das ist die bereits abgeleitete Beziehung für
den rein eindimensionalen Fall (d.h. ohne Sprünge in y- oder z-Richtung; so daß nicht 1/6
sondern 1/2 der Sprünge in die betrachtete x-Richtung führen). |
 |
Das ist zwar erfreulich, aber noch nicht was wir wollten.
Um einen Zusammenhang zwischen dem Mittelwert (<r2>)1/2 von r, oder dem wahrscheinlichsten
Wert (rwahr) von r und dem Diffusionskoeffizienten zu bekommen, müssen wir jetzt aber nur noch die gewünschte Größe aus der Lösung des 2. Fickschen Gesetzes berechnen,
da wir soeben gezeigt haben, daß diese Lösung vollständig äquivalent zur Betrachtung mit Hilfe der
reinen Statistik, des "Random Walks" ist. |
|
 |
Wir müssen
<x2> = 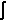 x2 · w(x) dx x2 · w(x) dx
(von 0 bis ¥).
berechnen. Dieses Integral ist im Tabellenmodul gelöst, das Ergebnis ist |
| | |
| |
|
|
|
 |
Für rwahr bekommen wir, mit den Wert aus der Tabelle
für eindimensionale Diffusion schlicht und ergreifend rwahr
= 0
Es ist an wahrscheinlichsten, ein Teilchen am Ursprung zu finden. Daran ändert sich auch nichts mit fortschreitender
Zeit - obwohl der mittlere Abstand der Teilchen vom Ursprung immer größer wird. |
 |
Damit ist die eindimensionale Diffusion erledigt. Aber
damit haben wir noch nicht - auch nicht im Prinzip
- die zwei und dreidimensionale Diffusion erledigt!
|
|
 |
Im Gegensatz zu vielen anderen physikalischen Phänomenen, bei den die Dimensionalität für
das Prinzip dessen was passiert keine große
Rolle spielt, gilt das nicht für die Diffusion: |
|  |
In der eindimensionalen Diffusion ist rwahr = 0 -
die Teilchen kommen nicht so recht vom Fleck. Das gilt nicht für höhere Dimensionen. Die Teilchen sind nicht mehr
mit größter Wahrscheinlicheit an der Quelle zu finden, und rwahr ist nicht mehr Null sondern
wächst mit der Wurzel aus der Zeit bzw. Sprungzahl - siehe die Tabelle |
 |
Den Zusammenhang zwischen Diffusionskoeffizient D und Diffusionslänge L
für zwei- und dreidimensionale Diffusion bekommt
man sofort aus der Überlagerung der eindimensionalen Lösungen. Dabei setzen wir aber voraus, daß die Diffusion
isotrop erfolgt, oder anders ausgedrückt, das D ein Skalar und kein Tensor zweiter Stufe ist. |
|
 |
Wir erhalten damit
- Eindimensional: D = L2/2t
- Zweidimensional: D = L2/4t
- Dreidimensional: D = L2/6t
|
| | |
© H. Föll (MaWi 1 Skript)


![]() Kurzfassung der Ableitung der Gauss Verteilung
Kurzfassung der Ableitung der Gauss Verteilung ![]() Eigenschaften des Random Walks in ein- zwei- und drei Dimensionen
Eigenschaften des Random Walks in ein- zwei- und drei Dimensionen ![]() Übung 6.3-1: Umgang mit Fakultäten und der Stirlingformel
Übung 6.3-1: Umgang mit Fakultäten und der Stirlingformel ![]() Wahrscheinlichster Abstand beim dreidimensionalen "Random Walk"
Wahrscheinlichster Abstand beim dreidimensionalen "Random Walk"