5.3.3 Gleichgewichtskonzentration von atomaren Fehlstellen in Kristallen

Herleitung der Gleichgewichtskonzentration von Leerstellen

	Mit dem Grundsatz der Minmierung der freien Enthalpie für thermodynamisches Gleichgewicht und der Boltzmannschen Entropieformel können wir:
		Verstehen, warum Kristalle immer einige atomare Fehlstellen enthalten.
		Exakt ausrechnen, wieviele es bei gegebenen äußeren Parametern sein werden.
	Dazu vergleichen wir einen perfekten Kristall mit einem Kristall, der einige Leerstellen enthält

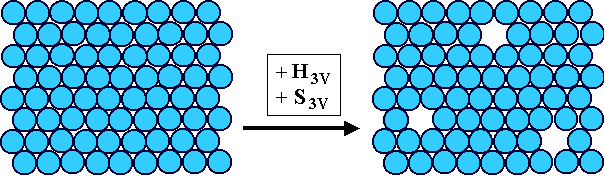
	Links ein perfekter Kristall, rechts ein Kristall mit 3 Leerstellen. Im Vergleich zu dem perfekten Kristall enthält er sowohl mehr Enthalpie als auch mehr Entropie.
		Da wir den Vergeich bei beliebigen Temperaturen machen, kann auch unser "perfekter" Kristall Entropie = Unordnung enthalten: Die Atome sitzen dann nicht still, sondern vibrieren mit statistisch wechselnder Frequenz und Amplitude, d.h. unordentlich, um ihre Gleichgewichtsposition. Wir ignorieren aber diesen Beitrag und betrachten nur die Entropie Sn die von n Leerstellen erzeugt wird.
	Die freie Enthalpie des perfekten Kristalls ist also ganz allgemein
		Gperfekt  =  H0  –  T · S0
	Die freie Enthalpie des Kristalls mit drei Leerstellen nennen wir G3V.
		Wir erhalten G3V aus der freien Enthalpie des perfekten Kristalls indem wir die zusätzliche Enthalpie H3V, die in den Leerstellen steckt zu H0 addieren und die zusätzliche Entropie S3V die durch die jetzt größerer Unordung entsteht zu S0. Wir erhalten
		G3V  =  (H0  + H3V)  –  T · (S0 + S3V)
		Es ist jetzt gut möglich, daß für eine bestimmte Zahl an Leerstellen die freie Enthalpie kleiner ist als für den perfekten Kristall, da der Zuwachs an T · S, Entropie mal Temperatur, den Zuwachs an Enthalpie überwiegen kann.
	Wie groß sind die Enthalpie- und Entropiebeiträge der Leerstellen? Zunächst zu der zusätzlichen Enthalpie, die benötigt wird um eine Leerstelle zu erzeugen.
		Formal muß man, um ein Atom zu entfernen, alle Bindungen des Atoms lösen. Dazu muß eine Energie, oder besser Enthalpie, aufgebracht werden, die ungefähr der gesamten Bindungsenergie entspricht. Die ungesättigten Bindungen der Nachbaratome der Leerstelle werden sich evtl. etwas umkonfgurieren, dabei wird dann wieder etwas Energie gewonnen.
		Insgesamt muß immer eine definierte Energiemenge, die Bildungsenthalpie HF(V) einer Leerstelle, aufgebracht werden (der Index "F" steht für "formation").
		Theoretisch ist HF(V) nur mit größter Mühe, und auch dann nur in nicht besonders guter Näherung errechenbar. Die Bildungsenthalpie einer Leerstelle in einem gegebenen Kristall ist aber trotzdem eine wohldefinierte Größe und im Zweifelsfall experimentell bestimmbar; wir setzen sie einfach als gegeben voraus.
		Man kann die Bildungsenthalpie auch mit dem (negativen) Energiegewinn identifizieren, der anfällt wenn wir die Leerstelle (gedanklich) wieder mit dem passenden Atom auffüllen.
	Damit können wir den Vergleich perfekter Kristall - Kristall mit n Leerstellen weiter quantifizieren, da wir zur Erzeugung von n Leerstellen die zusätzliche Enthalpie n · HF(V) brauchen. Hier der unmittelbare Vergleich
		Perfekter Kristall Kristall mit n Leerstellen 0 Leerstellen n Leerstellen Es gibt nur eine Anordnungsmöglichkeit der 0 Leerstellen bzw. der N Atome Es gibt viele Anordnungsmöglichkeiten der n Leerstellen. S0 = 0 Sn = S(n) ³ 0 Damit ist G0 = H0 – T · 0       = H0 Gn enthält die zusätzlichenEnthalpie um n Leerstellen zu bilden und die zusätzliche Entropie: Gn = H0 + n · HF(V) – T · S(n) Das Minimum der freien Enthalpie wird bei einer bestimmten Zahl von Leerstellen erreicht sein, diese Gleichgewichtszahl bestimmt sich aus dG(n) dn  = HF(V)  – T  · dS(n) dn  =  0

	Wir müssen nun nur noch S(n) berechnen. Mit der Entropieformel S = k · ln (pi/Spi) von Boltzmann ist das leicht (haha) möglich.
	Die Frage ist zunächst, wieviel Mikrozustände pi es zum Makrozustand "i = n Leerstellen verteilt auf N Plätze" gibt, wobei Leerstellen - im Gegensatz zu Würfeln - ununterscheidbar sind. Außerdem kann natürlich nur immer eine Leerstelle auf einem Platz sitzen. Die Zahl der Mikrozustände ergibt dann das pi für die Formel.
		Das ist eine Standardaufgabe aus der elementaren Kombinatorik. Die Formel dazu ist leicht herleitbar; wir betrachten dazu eine Tabelle der Möglichkeiten beginnend bei n = 0.
		n (= i) pn = Kommentar 0 1 Es gibt genau eine Möglichkeit keine Leerstelle zu haben: Alle Atome auf ihren Plätzen. 1 N Es gibt N Plätze für die 1. Leerstelle und damit N Mikrozustände 2 N · (N – 1) 2 Es gibt N Plätze für die 1. Leerstelle und noch N – 1 Plätze für die 2. Leerstelle. Auch wenn wir die Leerstellen unterscheiden könnten, bringt vertauschen jedoch nichts neues - die Anordnugen sind ununterscheidbar. Wir müssen also noch durch 2 dividieren 3 N · (N – 1) · (N – 2) 2 · 3 Vertauschen aller 3 Leerstellen bringt nichts neues da die möglichen Anordnungen auch ununterscheidbar sind, wir müssen deshalb durch 6 = 2 · 3 dividieren ... ... usw. n N · (N – 1) · (N – 2) · .... · (N – (n– 1)) 1 · 2 · 3 · ... · n Wir haben ein offenkundiges Bildungsgesetz. Der Nenner ist per definitionem n! gesprochen "Enn Fakultät" n N · (N – 1) · (N – 2) · .... · (N – (n – 1)) n! · (N – n)! (N – n)! Kleiner Trick: Wir erweitern mit (N – n)! und erhalten n N! n! · (N – n)!  =   æ è N n ö ø Das ist eine so häufige Formel, dass sie einen eigenen Namen und Symbol hat: æ è N n ö ø  =  Binomialkoeffizient

	Zur Berechnung von S(n) bräuchten wir noch p0 = S  pi.
		In aller Regel, wie schon ausgeführt, kann man sich aber die explizite Berechnung ersparen, wir werden gleich sehen warum. Die Entropieformel lautet jetzt
		Sn = k · ln pn p0  =  k · ln pn   –   k · ln p0
		Der zweite Term ist eine Konstante; wir können sie mit S ' bezeichnen. Die Entropieformel heißt dann Sn = k · ln pn  –  S ', oder mit der Formel für pn
		Sn = k · ln æ è N! n! · (N – n)! ö ø   –  S '  =  k · æ è ln N! – ln n! – ln (N - n)! ö ø   –  S '
	Damit ist die Errechnung der Gleichgewichtszahl an Leerstellen über dG(n)/dn = 0 jetzt eine mathematische Aufgabe geworden.
		Im wesentlichen ist dS(n)/dn zu bilden, also
		dSn dn  =  k · d dn æ è ln N! – [ln n! + ln (N – n)!] ö ø  –  S '
		Wir sehen sofort, daß der Term S' herausfällt, wir müssen ihn zur Berechnung von Gleichgewichten also gar nicht kennen - und das gilt ganz generell, wie schon gleich zu Beginn bemerkt!
	Die mathematische Aufgabe reduziert sich auf die Berechnung von
		d [lnn!] dn  +  d [ln(N – n)!] dn  =  0
	Da man Funktionen mit Fakultäten nicht so recht differenzieren kann (sie sind ja gar nicht stetig) ist es jetzt notwendig, einige Näherungen zu machen:
	Mathematische Näherung: Anwendung der einfachsten Version der Stirlingschen Formel für Fakultäten
		ln x!  »  x · ln x
		Diese simple Formel generiert nicht nur einen ganz gut passenden Zahlenwert für nicht zu kleine x, z.B. x = 17, sondern produziert auch eine stetige Funktion, d.h. sie liefert auch Werte für z.B. x = 17, 31. Was 17, 31! bedeuten mag lassen wir mal offen - aber auf jeden Fall können wir mit dieser Näherung jetzt differenzieren.
	Physikalische Näherung:
		n  <<  N       N – n  »  N
		Das ist gerechtfertigt, da die Zahl der Leerstellen immer viel kleiner sein wird als die Zahl der Atome.
	Weiterhin benutzen wir eine einfache Definition:
		n N  =  cV  =    absolute Konzentration an Leerstellen.
		Konzentrationen wie oben definiert haben keine Maßeinheit; die Konzentration 0,01 entspricht 1 % Leerstellen bezogen auf die Zahl der Atome. Statt Prozent benutzt man aber gerne folgende Abkürzungen:
		ppm = parts per million = 10– 6 ppb = parts per billion = 10– 9
		(Daß die amerikanische Billion der deutschen Milliarde (= 109) und nicht der deutschen Billion (= 1012) entspricht ist ein Quell ständiger Irrtümer in allen deutschen Zeitungen.
		Gebräuchlich ist auch noch
		ppt = parts per trillion = 10– 12 (nicht mit "parts per thousand" zu verwechseln; das gibt es nicht als Abkürzung!!!). ppqt = parts per quatrillion = 10– 15
		Kleinere Konzentrationen sind i.a. nicht meßbar; deshalb gibt es keine gebräuchlichen Abkürzungen nach ppqt - wohl aber für Vorsilben!
		Man kann Konzentrationen natürlich auch auf ein bestimmtes Volumen beziehen (dann ist die Einheit cm– 3), auf 1 mol einer Substanz oder auf Partialdrücke. Man muß höllisch aufpassen, daß man hier keine Fehler macht - im Link gibt es dazu viele Details.
	Die nun recht einfache Mathematik überlassen wir einer Übungsaufgabe.
		Übung 5.3-2 Berechnung der Gleichgewichtskonzentration an Leerstellen

	Als Ergebnis erhalten wir für die Leerstellenkonzentration im thermodynamischen Gleichgewicht
		cV  =  exp –   HF(V) kT
		Das ist die in einem vorhergehenden Kapitel bereits postulierte Formel. Aber jetzt haben wir sie aus "first principles" hergeleitet!
	Dies bedeutet, daß für thermodynamisches Gleichgewicht eine ganz bestimmte Konzentration cV(T) an Leerstellen benötigt wird.
		Kristalle ganz ohne Leerstellen bei endlicher Temperatur oder mit der falschen Anzahl, sind nicht im chemischen GG! Über chemisches GG reden wir deshalb, weil wir GG bezüglich einer Teilchenzahländerung ausgerechnet haben. Die "Teilchen" in diesem Fall waren Leerstellen.
		Der jeweilige Wert der Gleichgewichtskonzentration sinkt exponentiell (Minuszeichen im Exponenten beachten!) mit der Bildungsenthalpie und steigt exponentiell mit der Temperatur. Wer Probleme mit der Visualisierung von Exponentialfunktionen hat, betätigt den Link
	Wir können diese ausführliche Betrachtung jetzt sofort verallgemeinern, denn sie gilt analog auch für andere atomare Fehlstellen:
		Nehmen wir die Bildungsenthalpie der Eigenzwischengitteratome HF(i) , haben wir die Gleichung für die Gleichgewichtskonzentration an Eigenzwischengitteratomen.
		Nehmen wir eine spezifische Enthalpie zur Beschreibung des Einbaus eines Fremdatoms, HL(FA), beschreiben wir die Löslichkeit eines Fremdatoms, d. h. die optimale Konzentration bei einer bestimmten Temperatur. HL(FA) beschreibt dabei die Energie die am aufbringen muß, um ein Fremdatom ins Gitter einzubauen.
		Hier muß man allerdings ein bißchen aufpassen. Während man zur Erzeugung, d.h. zum Einbau einer Lehrstelle oder eines ZGA immer Energie aufwenden muß, kann HL(FA) auch mal negativ sein, d.h. man gewinnt Energie durch Einbau eines Fremdatoms (Kristallatome haben lieber ein Fremdatom als Nachbar, als eines der eigenen Sorte). Auch kann HL(FA) sehr klein sein (d.h. es ist dem Kristall dann ziemlich egal, wer auf den Gitterplätzen sitzt).
	Solange die Konzentrationen klein sind, d.h. die diversen atomaren Fehlstellenarten sich gegenseitig "nicht sehen", sind alle Konzentrationen einfach additiv - GG verlangt nach der jeweils richtigen Konzentration aller im System machbaren atomaren Fehlstellen.
	In jedem Fall erfordert das Minimum der freien Enthalpie, daß eine bestimmte Konzentration an atomaren Fehlstellen vorhanden sein muß. Für hohe Bildungs- oder Löslichkeitsenthalpien oder niedrige Temperaturen kann diese Konzentration beliebig klein werden, mathematisch Null wird sie jedoch nie!
		Physikalisch Null ist eine Konzentration aber spätestens dann, wenn weniger als ein atomarer Defekt auf alle Atome des betrachteten Kristalls kommen. Dies ist bei makroskopischen (mit dem bloßen Auge sichtbaren) Kristallen rund und roh bei Konzentrationen von c » 10– 21 der Fall.
		Meßtechnisch sind allerdings schon Konzentrationen von c £ 10– 10 meist nicht mehr direkt erfaßbar. Das schließt aber nicht aus, daß atomare Defekte in derart kleinen Konzentrationen trotzdem noch die Eigenschaften eines Materials beeinflussen können.

	Entstehung und Vernichtung von intrinsischen atomaren Fehlstellen
	Die Thermodynamik schreibt einem Kristall zwingend vor, wieviele Leerstellen und Eigenzwischengitteratome er im thermodynamischen Gleichgewicht und einer gegebenen Temperatur haben muß. Bei einem Wechsel der Temperatur ändert sich die Gleichgewichtskonzentration, und das bedeutet, dass atomare Fehlstellen entweder erzeugt oder vernichtet oder werden müssen - je nachdem ob wir die Temperatur erhöhen bzw, erniedrigen
		Wie kann ein Kristall in der Realität AF's erzeugen oder vernichten? Ein Atom kann ja nicht einfach so verschwinden (und an der Oberfläche wieder auftauchen) wie wir das mit der Mathematik postulieren.
		Umgekehrt, wie kann eine vorhandene Leerstelle verschwinden? Indem sie mit einem Eigen-ZGA rekombiniert, OK; aber da es in der Regel sehr viel weniger ZGA's als Leerstellen gibt, wird das nicht viel nützen.
	Die Antwort ist einfach im Prinzip und komplex in der Praxis:
		Erzeugung und Vernichtung von AF's geschieht mit Hilfe anderer Defekte; insbesondere Versetzungen und Korngrenzen. Beide Defektsorten können AF's emittieren oder absorbieren.
		In Kapitel 10 werden wir lernen wie das geht (und was dabei mit den Korngrenzen und Versetzungen geschieht). Die Links führen auf Unterkapitel mit relevanten Bildern, die aber auch schon in dem hier diskutierten Zusammenhang sofort verständlich sind: AF's und Versetzungen AF's und Korngrenzen
		Darüberhinaus können AF's formal verschwinden, indem sie sich zu größeren Defekten, z.B. "Voids" oder Versetzungsringen zusammenlagern - das hatten wir schon früher angesprochen.
	.Wenn man ein bißchen weiterdenkt, wird jedoch sofort klar, dass für alle diese Prozesse Zeit benötigt wird, da die AF's erstmal die "Partner finden (oder verlassen) müssen. Dazu müssen sie diffundieren.
		Die Einstellung eines neuen Gleichgewichts wird also schnell erfolgen können, falls die AF's sehr beweglich sind. Falls sie aber nur langsam und träge im Gitter herumdiffundieren, kann es auch sehr lange dauern - Stunden, ein Menschenalter, ein Millenium, ein Alter des Universums.
	Was wir hier betrachten ist der Weg ins Gleichgewicht - die Kinetik. Sie wird uns ein eigenes Kapiutel wert sein!

	Einige Zahlen
	Wie groß sind reale Bildungsenergien und Konzentrationen?
		Zunächst gilt (fast) immer
		HF(i)  >  HF(V)
		d.h. die Konzentration an Leerstellen wird i.d.R. viel größer sein als die Konzentration an Eigenzwischengitteratomen. Die große Ausnahme hier, wie auch bei vielen anderen Eigenschaften, ist Silizium. Im Link sind einige der bemerkenswerten speziellen Eigenschaften von Si zusammengefaßt.
		Typische Werte für die Bildungsenthalpien der Leerstellen sind:
		Kristall HF(V) [eV] Ag 1,1 Al 0,76 Au 0,98 Cu 1,0 Si ? 2,0 - 4,5 nicht eindeutig geklärt
	Damit erhält man als groben Richtwert für die maximale Leerstellenkonzentration am Schmelzpunkt der gebräuchlichen Metalle, cV(max) »» 10– 4
		Bei Si, anderen Halbleitern und kovalent gebundenen Kristallen ist die maximale Konzentration aber viel kleiner und nicht direkt meßbar - und trotzdem von überragender Wichtigkeit, wie wir noch sehen werden.
	In nächsten Unterkapitel wollen wir uns noch etwas detaillierter mit der Konzentration atomarer Fehlstellen beschäftigen, wie sie durch die hier abgeleitete Formel beschrieben wird.
	Fragebogen Multiple Choice Fragen zu 5.3.3

© H. Föll (MaWi 1 Skript)