|
Die verschiedenen Defekttypen sind nicht unabhängig voneinander, sondern
stehen in vielfältiger und dynamischer Beziehung zueinander. Dazu einige Beispiele, die sofort einleuchten und die
im vorherigen Kapitel schon angeklungen sind: |
 |
Dreidimensionale Defekte sind notwendigerweise
von zweidimensionalen Defekten begrenzt, denn ihre Oberfläche ist per definitionem
eine Phasengrenze. Das hat sofortige weitreichende Konsequenzen: |
|
 |
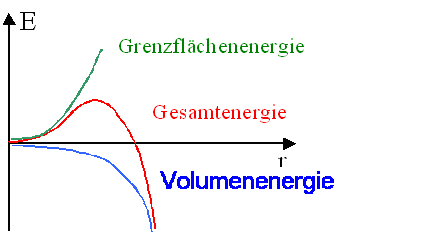
Die Gesamtenergie des dreidimensionalen Defekts
ist immer gegeben durch die Energie die im Defektvolumen steckt plus der Energie der Phasengrenze.
|
|
 |
Die Energie des Volumens kann man als Nettobilanz in einem Energievergleich auffassen:
x Frematome sind statistisch im Gitter verteilt oder in einer Ausscheidung
konzentriert. Bei tiefen Temperaturen ist i.d.R. die Ausscheidung günstiger, die Volumenenergiebilanz ist dann negativ.
Die Gesamtenergie des Kristalls sinkt also wenn sich die Verunreinigungen ausscheiden; für kugelförmige Ausscheidungen
mit Radius r nimmt sie also mit – const. · 4/3pr3 ab.
|
|
 |
Die Energie der Phasengrenzfläche ist aber immer
positiv, ihr Anteil an der Gesamtenergie wächst dementsprechend mit g · 4pr2.
Graphisch sieht das immer so aus: |
| |
|
|
 |
Die mit r3 abnehmende Volumenenergie "gewinnt"
mit wachsendem Radius immer gegenüber der mit r2 wachsenden
Oberflächenenergie. Aber für kleine Radien ist die Grenzflächenenergie
der bestimmende Term. |
 |
Dies bedeutet, daß bei der Bildung einer Ausscheidung die Energie immer erst anwächst, bevor sie abnimmt! Der energetisch günstigere Zustand kann damit
nur durch Überwinden einer Energiebarriere erreicht werden, es
bedarf einer Nukleation, einer Keimbildung der Ausscheidung,
bevor durch Wachstum der Ausscheidung immer mehr Energie gewonnen werden kann, so daß das Wachstum "von alleine"
abläuft. |
|
 |
So einfach ist das Konzept einer Enrgiebarriere und der ungeheuer wichtige Prozeß der Keimbildung zu verstehen! |
 |
Dreidimensionale Defekte können aber
auch durch Diffusion und Zusammenlagerung (= Agglomeration, "clustern") von nulldimensionalen
Defekten entstehen. |
|
 |
Treffen sich viele Leerstellen an einem Platz, entsteht ein Void,
das leuchtet sofort ein. Auch hier ist der dreidimensionale Defekt durch den zweidimensionalen Defekt "Oberfläche"
begrenzt, die obigen Überlegungen treffen voll zu. |
|
 |
Sebstverständlich können auch auch substitutionelle oder interstitielle Fremdatome
per Diffusion agglomerieren; es resultiert eine Ausscheidung. |
| |
|
Zweidimensionale Defekte und eindimensionale
Defekte |
| |
|
 |
Etwas weniger einleuchtend als obige Beziehungen ist die folgende Aussage: Stapelfehler enden an inneren oder äußeren Oberflächen oder
sind durch eindimensionale Defekte (= Versetzungen) begrenzt. |
|
 |
Um das zu verstehen, denken wir uns die beiden Stapelfehlertypen wieder durch das vorhergehende Rezept konstruiert: Aufschneiden, Ebene wegnehmen oder zufügen, dann wieder
zusammensetzen. Aber jetzt schneiden wir nur in einen Teil des Kristalls. Dann entstehen folgende Defekte in kompletter
Analogie zu den im vorherigen Unterkapiteln gezeigten Bildern: |
|
|
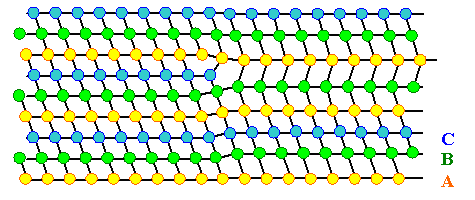 |
Die C - Ebene fehlt im rechten Teil,
wir haben einen intrinsischen
Stapelfehler.
Er wird offenbar von einer Stufenversetzung berandet |
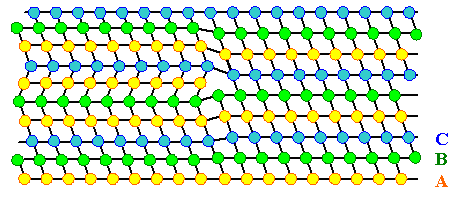 |
Eine A - Ebene ist im linken Teil zusätzlich enthalten,
wir haben einen extrinsischen Stapelfehler |
| Beide Stapelfehler sehen ziemlich ähnlich aus, sind
aber verschieden - genau hinschauen! Sie sind längs der Schnittlinie durch einen eindimensionalen Defekt berandet -
eine Art Stufenversetzung. |
|
 |
Gezeigt sind dieselben Bilder,
die schon im vorhergehenden Unterkapitel 4.1.5 die Stapelfehler illustrierten; nur
im Sinn des obigen Rezepts weitergezeichnet. Die Berandung der Stapelfehler sieht sehr nach einer Stufenversetzung aus.
Der zugehörige eindimensionale Defekt ist auch eine (Stufen)versetzung, aber keine richtige oder vollständige Versetzung, sondern eine sogenannte Partialversetzung. |
|
 |
Der Burgersvektor dieser Partialversetzungen ist nämlich kein
Translationsvektor des Gitters! Würde man im obigen Bild einen Umlauf machen, der einem Burgersumlauf entpricht, findet
man b = a/3<111> als Burgersvektor der Partialversetzung, also keinen Translationsvektor.
|
|
 |
Einfacher erhält man dieses Ergebnis, wenn man das Volterra Rezept anwendet (Schneiden, Verschieben um a/3<111>, Material einfüllen oder entnehmen,
zusammenfügen, feststellen, dass die Schnittflächen nicht "passen", den resultierenden Stapelfehler,
wenn man'as trotzdem tut, in Kauf nehmen). Partialversetzungen mit diesem Burgersvektor heißen allgemein auch Frank - Versetzungen. |
|
 |
Um das ganze noch etwas zu verkomplizieren, sei nur zur Illustration noch hinzugefügt:
Ein Stapelfehler kann auch noch durch eine andere Sorte von Partialversetzungen berandet werden, durch sogenannte Shockley - Versetzungen
mit den Burgersvektor a/6<112>. |
|
 |
Wer das genauer wissen möchte, betätigt den Link. |
| |
|
|
Stapelfehler und atomare Fehlstellen |
| |
|
 |
Wir ahnen schon die nächste Beziehung: Stapelfehler in
fcc - Kristallen (inkl. Berandung durch eine Franksche Partialversetzung) können durch Agglomeration
von Leerstellen oder Eigenzwischengitteratomen auf {111} - Ebenen entstehen. |
|
 |
Leerstellenagglomeration auf einer {111} - Ebene entspricht dem Herausnehmen
einer Ebene, es wird ein intrinsischer Stapelfehler erzeugt. |
|
 |
Die Agglomeration von Zwischengitteratomen auf einer {111} - Ebene schiebt eine zusätzliche
Ebene ein, es entsteht ein extrinsischer Stapelfehler. |
 |
In der Realität ist dieser Prozeß nicht selten; es entsteht i.d.R.
ein kleines Leerstellen- bzw. Zwischengitteratomscheibchen; ein Querschnitt sieht so aus: |
|
|
|
 |
Links ein "Leerstellenring"; rechts ein Zwischengitteratomring. |
| |
|
|
Versetzungen und atomare Fehlstellen |
| |
|
 |
Die Beziehung zwischen Versetzungen und atomaren Fehlstellen ist die Grundlage
der Metallurgie. |
|
 |
Aus relativ weichen reinen Metallen wird durch "Verunreinigen" oder Legierung das
harte Gebrauchsmetall. |
|
 |
Weiches Schmiedeeisen und ein bißchen Kohlenstoff macht harten Stahl -
allerdings mit noch tausend Tricks drumherum; wenn man den alten Schmiedegeschichten
glaubt. |
 |
Es ist ganz einfach - im Prinzip. |
|
 |
Versetzungsbewegung macht plastische Verformung, und das geht umso einfacher ("weiches
Material"), je leichter es ist, die Versetzungen zu bewegen. |
|
 |
Atomare Fehlstellen aller Arten (und die von ihnen stammenden Ausscheidungen) behindern die
Versetzungsbewegung, das Material wird härter. |
 |
Allerdings sollte man die Versetzungsbewegung nicht ganz unmöglich machen
- denn dann ist das Material spröde, und das ist auch nicht gut. |
|
 |
Denn ein Schwert sollte sich weder verbiegen ("weich"), noch brechen ("spröde"),
sondern allenfalls ein bißchen elastisch biegen oder etwas eindellen. |
| |
 |
Jetzt wollen wir es genug sein lassen. Wir ahnen, daß es weitere Beziehungen
gibt (z. B. zwischen Versetzungen und Korngrenzen). Statt weitere Beispiele zu betrachten, nehmen wir nur einen Merksatz
mit, der sehr große Bedeutung hat |
|
|
Defekte sind oft korreliert und treten gemeinsam auf.
Aus "kleinen" Defekten können "große"
Defekte entstehen |
|
 |
Der letzte Satz wird und wurde in der Halbleitertechnik oft leidvoll erfahren:
Aus einer Handvoll Fremdatome, die atomar verteilt niemand stören würden, entwickeln sich wenn man Pech hat, massive
Defekte, die das Bauelement "killen". Statt Umsatz produziert man Abfall. Einige Beispiele dazu im Link. |
 |
Zum Schluß noch eine kleine Illustration gekoppelt mit einer Übung |
| |
| Übung
4.2-3 |
| Defekte finden, identifizieren und Varianten diskutieren |
|
 |
Und dann selbstredend noch der "Multiple Choice test; |
| |
|
© H. Föll (MaWi 1 Skript)