 |
Versetzungen sind die einzigen
eindimensionalen oder linienhafte Defekte in Kristallen; es gibt sie aber in vielen Varianten. Sie sind erfahrungsgemäß
nicht ganz einfach zu verstehen. Wir wollen hier aber nur einige ganz allgemeine Eigenschaften behandeln, denn: |
|
 |
Versetzungen sind die für die gesamte plastische Verformung kristalliner Materialien verantwortlichen
Defekte und damit insbesondere für alle Metalle. |
|
 |
Gäbe es keine Versetzungen in Kristallen, wären alle Kristalle
spröde wie Glas! Die gesamte metallverarbeitende Industrie mit all ihren Produkten würde nicht existieren. |
|
 |
Andererseits: Versetzungen sind absolut tödliche
Defekte für viele Halbleiterbauelemente. Könnte man nicht vollständig versetzungsfreie Siliziumkristalle
herstellen, gäbe es keine Mikroelektronik. |
 |
Grund genug, sich Versetzungen etwas näher anzuschauen. Zunächst anhand
der Struktur der am einfachsten zu zeichnenden Versetzung, der sog. Stufenversetzung.
|
|
 |
Hier ist das schon vorher erwähnte
Rezept zur Generierung einer Stufenversetung: |
|
|
 |
 |
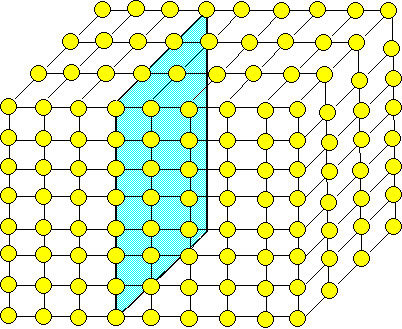
Perspektivische dreidimensionale Sicht eines Gitters/Kristalls:
Eine Ebene aus einer Ebenenschar {hkl} mit den
auf ihr sitzenden Atomen ist herausgegriffen
und blau markiert. |
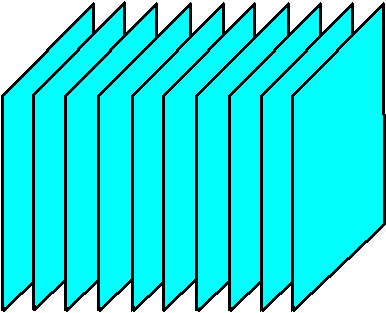
Darstellung des Kristalls nur durch die
gewählte Ebenenschar
zur zeichnerischen Vereinfachung |
 |
 |
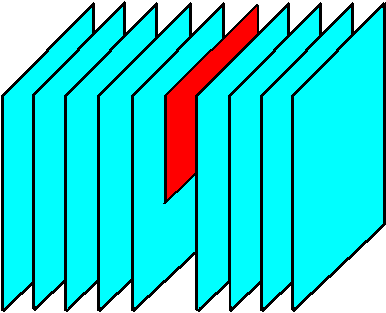
Mit einem fiktiven Messer wurde ein Teil
einer Ebene entfernt. |
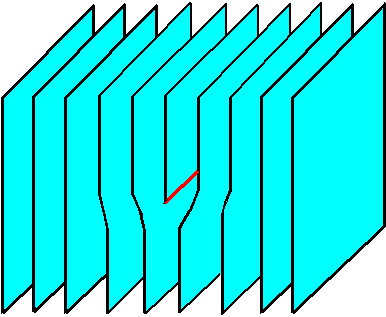
Die beiden Kristalloberflächen links und rechts der
Schnittfläche werden
wieder zusammengefügt; um den
Versetzungskern herum muß das Gitter
dabei elastisch
verspannt werden. |
|
 |
Mit dieser sehr künstlichen Konstruktion ist jedenfalls ein eindimensionaler
Defekt entstanden. Denn entlang der Versetzungslinie (im letzten Bild rot gekennzeichnet) stimmt die Symmetrie des Gitters
prinzipiell nicht mehr. Etwas weiter weg ist, von elastischen Verzerrungen abgesehen, jedoch alles in Ordnung - und elastische
Verzerrungen für sich sind keine Defekte! |
|
 |
Zunächst sollte jeder sich durch eine kleine Skizze davon überzeugen,
daß diese Aussage stimmt. Man muß nur im obigen Bild wieder die Atome einfüllen. |
|
 |
Danach fassen wir Mut, denn trotz der künstlichen
Erzeugung der obigen Stufenversetzung sehen reale Stufenversetzungen genau so aus. Dies kann mit elektronenmikroskopischen
Bildern, auf denen man bei sehr hoher Vergrößerung (am Rande des Möglichen) die Projektionen der Netzebenen
direkt sehen kann, sehr schön illustriert werden; ein Beispiel
ist im Link zu sehen. |
 |
Aus dem simplen Bild weiter oben lassen sich schon einige Folgerungen ableiten: |
|
 |
Zur Beschreibung einer Versetzung gehört immer eine
Aussage über die Versetzungslinie. Bei uns verläuft diese Linie gerade, aber das ist künstlich. Selbst mit
unserm fiktiven Messer hätten wir ja auch krumm in den Kristall schneiden könnnen. |
|
 |
Eine Versetzung kann nicht im Inneren des Kristalls enden.
Eine Schnittlinie kann das auch nicht. Der aufgeschnittenen Bereich hat immer eine Umrandung (= die Versetzungslinie), die
entweder bis zur Oberfläche läuft oder einen geschlossenen Kreis bildet. |
|
 |
Nach dem Schneiden mußten wir die Schnitthälften wieder zusammenfügen; dazu
war eine Verschiebung der Schnittebenen nötig. Die "Stärke" dieser Verschiebung definiert uns die "Stärke" der Versetzung. Hätten wir zum Beispiel zwei Ebenen herausgeschnitten,
hätten wir doppelt so viel verschieben müssen, um die Schnitthälften wieder zusammenzufügen. |
 |
Damit können wir jetzt die allgemeinste Definition aller
möglichen Versetzungen angehen; sie stammt von Volterra,
der 1907 aus allgemeinen elastizitätstheoretischen Überlegungen heraus die folgenden Betrachtungen anstellte.
Die Versetzung selbst wurde erst 1934 als tatsächlicher Defekt postuliert! |
 |
Volterra verallgemeinerte den Umgang mit dem fiktiven
Messer das wir mal Volterra Messer nennen. In moderner Notation sieht das
Rezept so aus: |
|
|
| 1. (Fiktiver) Schnitt in den Kristall;
die Schnittlinie entspricht dem Linienvektor t der zu bildenden Versetzung |
1a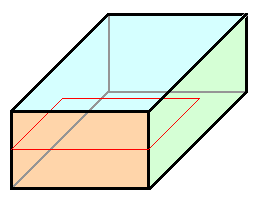 |
Die Schnittlinie im Material definiert die Versetzungslinie;
sie kann nicht im Material enden. Der Schnitt bildet immer eine durch einen geschlossenen Ring berandete Fläche; in
unserer Konstruktion verlaufen 3 der 4 Schnittlinien auf der Oberfläche. |
2. Verschieben der beiden Schnittebenen um einen beliebigen Translationsvektor
des Gitters. Der gewählte Translationsvektor ist für die entstehende Versetzung charakteristisch und heißt
Burgersvektor
b nach dem ErfinderBurgers; das Vorzeichen hängt von einer hier unwichtigen Konvention
ab. Gezeigt sind drei mögliche Verschiebungen. 2a und 2b sind problemlos, da die Verschiebung in der
Schnittfläche liegt; für 2c müssen wir noch was tun. |
2a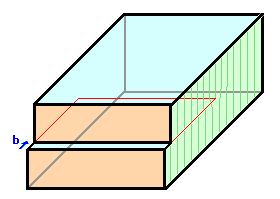 |
2b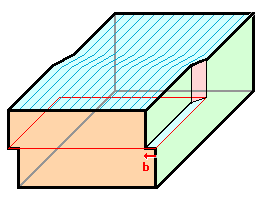 |
2c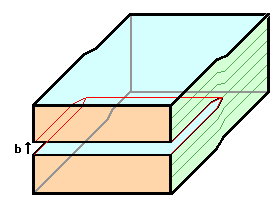 |
3. Liegt die Verschiebung nicht in der Schnittfläche, brauchen wir eine
zusätzliche Regel. Es gilt einfach: Material so entnehmen oder einfüllen, daß die Schnittflächen wieder
aufeinander passen. |
4. Wir stellen wieder eine perfekten Kristall
her - mit Ausnahme der Umgebung der Versetzungslinie - indem wir die Schnittflächen wieder "verschweißen".
Da der Burgersvektor ein Translationsvektor des Gitters ist, passen die beiden Hälften immer
exakt aufeinander
|
 |
|
 |
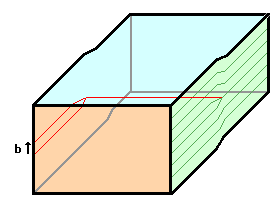
Dieses Rezept klappt immer. Da der Verschiebungsvektor
ein Translationsvektor des Gitters war, passen die Schnittflächen überall perfekt zusammen -außer
entlang der im Material verlaufenden Schnittlinie, der Versetzungslinie. Es ist
ein eindimensionaler Defekt, entstanden - eine Versetzung. Wir erkennen die schon eingeführte
Stufenversetzung in Bild 1a wieder, aber auch neue Gebilde wie die Schraubenversetzung
in Bild 1b. |
|
 |
Die Versetzung ist dabei eindeutig durch ihren Linienvektor t
= t(x,y,z) und ihren Burgersvektor b = const. =
Translationsvektor des Gitters definiert, mit Linienvektor = Schnittlinie; Burgersvektor
= Verschiebungsvektor. |
|
 |
Der Burgersvektor ist für eine gegeben
Versetzung überall gleich da es nur eine Verschiebung
der Schnittflächen relativ zueinander gibt. Der Linienvektor kann
jedoch (als Tangente an die Versetzungslinie = Schnittlinie) an jedem Punkt anders sein,
da wir ja auch willkürliche Schnitte machen könnten. |
|
 |
Stufen- und Schraubenversetzung (mit einem Winkel a(t,
b) = 90° bzw. 0° zwischen dem Linienvektor t und Burgersvektor b der Versetzung)
sind Grenzfälle des allgemeinen Falls einer gemischten
Versetzung, mit Winkel a(t, b) = beliebig. |
 |
Mit dieser Definition kann man eine verwirrende Vielfalt möglicher Versetzungen
erzeugen. In der Realität gibt es sogar noch Untervariante, die mit der hier wiedergegebenen einfachen
Volterra Definition gar nicht abgedeckt sind. So tief wollen wir hier aber noch nicht in die Versetzungstheorie eindringen,
sondern uns nur noch drei Eigenschaften des Burgersvektor anschauen: |
|
 |
1. Der Burgersvektor gibt direkt die Größe der Stufe an, die durch die Erzeugung
der Versetzung auf der Kristalloberfläche entstanden ist. Dies ist aus den obigen Bildern direkt ablesbar. |
|
 |
2. Das Verfahren kann umgedreht werden: Ist die atomare Struktur einer Versetzung gegeben
(z.B. aus einem elektronenmikroskopischen Bild), kann der zunächst ja nicht bekannte Burgersvektor aus einem Burgersumlauf
bestimmt werden. Das Rezept ist einfach und in der folgenden Graphik dargestellt: |
|
 |
3. Burgersvektor und Linienvektor spannen die Gleitebene auf. Nur auf dieser Ebene kann sich die Versetzung bewegen ohne daß Material
eingefüllt oder herausgenommen werden muß. Das ist leicht einzusehen, denn Versetzungsbewegung
heißt, den Schnitt mit dem Volterra Messer fortzuführen. |
| |
 |
 |
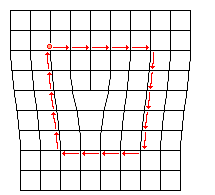
Führe einen beliebig gestalteten
geschlossenen Umauf
von Gitter-
punkt zu Gitterpunkt um die
Versetzung durch. |
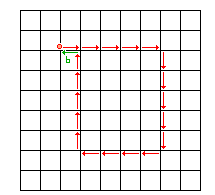
Führe exakt denselben Umlauf in
einem Referenzkristall
durch - der
Umlauf wird sich jetzt
nicht mehr schließen. |
|
 |
Aber jetzt zum Dreh- und Angelpunkt der Bedeutung von Versetzungen für die
Menschheit! Wir werden dies in Kap. 8 noch ausführlicher behandeln,
hier geht es um das Prinzip |
|
|
| Plastische Verformung aller Kristalle erfolgt ausschließlich durch
die Erzeugung und Bewegung von Versetzungen |
|
 |
Plastische, d.h. bleibende
Verfomung bedingt, daß Teile eines Kristalls sich gegenüber anderen Teilen
verschoben haben. Dies geschieht immer nur dadurch, daß Versetzungen durch den
Kristall laufen. |
|
 |
Betrachten wir z.B. Bild 2a als einen Zustand,
bei dem die durch den Schnitt definierte Versetzung von der orangefarbigen Oberfläche aus in den Kristall hineingelaufen
ist, so wäre nach weiterem Durchlaufen der Versetzung "nach hinten", der obere Teil des Kristall gegenüber
dem unteren um genau einen Burgersvektor verschoben sobald die Versetzung an der Rückseite austritt. |
|
 |
Dies schauen wir uns im nächsten Unterkapitel etwa genauer an. |
 |
Vorher aber noch eine kleine Anregung: (Stufen)versetzungen, wenn man mal weiß
was das ist, findet man im zweidimensionalen überall, wo es periodische Strukturen
gibt: Auf mit Dachziegeln gedeckten Hausdächern, im Muster der Pflastersteine - Augen offen halten. |
|
 |
Dann auch noch in periodischen Anordnungen, die nicht jeder zu Gesicht bekommt, z.B. im "Void lattice" wie es in manchen Kristallen nach heftiger Bestrahlung mit z.B. He
ensteht: Schießt man genügend He in einen Kristall, entstehen kleine gasgefüllte Blasen - englisch
voids genannt. Das sind dreidimensionale Defekte (siehe Kap. 4.1.6),
und manchmal ordnen sich diese Voids periodisch an; sie bilden einen Void-Kristall. Und dieser Void-Kristaln hat Kristallgitterdefekte,
z.B. Versetzungen. Wer's nicht glaubt, betätigt den Link. |
| |
|
© H. Föll (MaWi 1 Skript)










