4. Reale Kristalle

4.1 Allgemeine Definitionen und Klassifikation von Defekten

4.1.1 Was sind Defekte?

	Es gibt nirgendwo im Universum einen perfekten Kristall! Denn jeder Kristall hat eine Oberfläche und für die Atome auf der Oberfläche ist die Umgebung anders als für Atome im Volumen - die Oberfläche ist somit ein Defekt. Reale Kristalle sind damit Kristalle, die Defekte enthalten.
	Verstehen wir die Oberfläche als Defekt eines Idealkristalls, können wir zu einer einfachen Definition für Defekte in Kristallen gelangen:
		Falls um ein beliebig herausgegriffenes Atom die unmittelbare Umgebung (im zeitlichen Mittel) eine andere prinzipielle Symmetrie hat als die Umgebung eines Referenzatom in einem perfekten Teil des Kristalls, haben wir am Aufpunkt einen Defekt. Für ein Atom auf der Oberfläche eines Kristalls ist diese Bedingung zweifellos erfüllt.
	Es gibt also prinzipiell keine perfekten Kristalle. Das ist auch gut so, denn schon Kristalle, die außer der Oberfläche sonst keine Defekte mehr enthalten, sind langweilig. Sie haben einen Satz von Eigenschaften der unveränderlich feststeht, und wären damit technisch ziemlich uninteressant.
		Ihr einziger (oft sehr wichtiger) Zweck kann allenfalls darin bestehen, daß man ausgehend von einem möglichst perfekten Kristall sich leichter tut, Defekte gezielt in den Kristall einzubauen. Das macht man, weil die meisten der interessanten Eigenschaften von Kristallen von Kristallgitterbaufehlern - kurz Defekte genannt - bestimmt werden.
		Defekte bestimmen z.B. ob ein Stück Eisen sich leicht oder schwer verformt, hart oder weich ist, leicht bricht oder sich zäh verhält, leicht oder schwer korrodiert, sich hart- oder weichmagnetisch verhält, schnell oder nur langsam ermüdet - die Liste wäre verlängerbar. Die gesamte Halbleitertechnologie dreht sich um die Manipulation von Defekten in Halbleitern wie Silizium oder GaAs. Wir müssen uns also mit Defekten in Kristallen befassen.
	Die obige Definition bietet einen einfachen Zugang zu strukturellen (im Gegensatz zu elektronischen) Aspekten von Defekten. Um das Thema etwas einzuengen, zunächst zwei Bemerkungen dazu, welche Abweichungen vom mathematisch idealen Gitter oder Kristall keine Defekte in unserem Sinne sind:
		Die thermischen Schwingungen der Atome um ihre Gleichgewichtslage zählen nach obiger Definition nicht als strukturelle Defekte - im zeitlichen Mittel sind sie Null.
		Elastische Verbiegungen des Gitters, also lokal leicht veränderte Gitterkonstanten und damit Bindungslängen, sind ebenfalls keine Defekte, da sich die lokale Symmetrie dadurch nicht im Prinzip geändert hat, sondern allenfalls einige Zahlenwerte, z. B. bei den Translationsvektoren des Gitters.
	Defekte kann man zunächst in vier große Klassen einteilen, deren Ordnungskriterium die Dimensionalität des Defekts ist: Wir unterscheiden:
		Nulldimensionale Defekte (oder "Punktdefekte" "Punktfehler", atomare Defekte) Symmetrieverletzung nur in Bereichen mit Ausdehnung ca. "Null", d.h. in einem Bereich mit atomaren Dimensionen. Eindimensionale Defekte (oder "Versetzungen", "Liniendefekte") Entlang einer Linie (die nicht gerade verlaufen muß, sondern willkürlich gekrümmt oder in sich geschlossen sein kann) ist die Symmetrie verletzt. Zweidimensionale Defekte (oder "Flächendefekte") Auf einer Fläche (beliebig gekrümmt) ist an jedem Punkt die Symmetrie verletzt. Dreidimensionale Defekte (oder "Volumendefekte") In einem beliebigen Volumen liegt an jedem Punkt eine andere Symmetrie vor.

	Diese noch etwas abstrakte Definition wird sofort klar, wenn wir uns typische Vertreter dieser vier Defekttypen anschauen - sozusagen die Leitfossilien:
		Die Leerstelle für nulldimensionale Defekte: Ein Atom fehlt irgendwo im Kristall, der entprechende Platz ist leer.
		Die Stufenversetzung für eindimensionale Defekte: Zwischen zwei Kristallebenen ist teilweise eine dritte eingezwängt. Diese zusätzliche Ebene im Kristall endet entlang einer Linie; dies Linie definiert den eindimensionalen Defekt "Stufenversetzung". Ein Bild dazu kann im Link angeschaut werden; es wird jedoch empfohlen, zunächst zu prüfen, ob man sich den Defekt mit obiger Beschreibung selbst vorstellen oder skizzieren kann!
		Die Korngrenze für zweidimensionale Defekte: Zwei beliebig zueinander orientierte Kristalle sind längs einer Ebene - der Korngrenzenebene - verbunden.
		Die Ausscheidung für dreidimensionale Defekte: In einem Kristall der Sorte 1 sitzt ein Kristall (oder amorpher Körper) der Sorte 2.
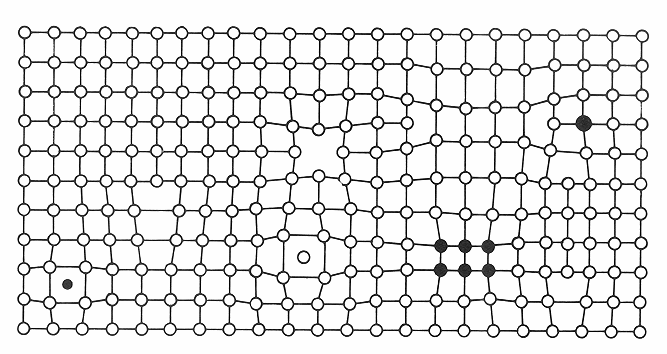
	Dazu noch ein Bild von Gitterdefekten (nicht Kristalldefekte - selbst herausfinden warum nicht), das sich allmählich zu einem Klassiker entwickelt. Es ist eine gute Übung, mal selbst zu versuchen, die obige Klassifikation den Buchstaben zuzuordnen.
	In den nächsten Unterkapiteln schauen wir uns diese Defekte etwas genauer an.
		Vorher aber eine schnelle Übung:
		Fragebogen Multiple Choice Fragen zu 4.1.1

© H. Föll (MaWi 1 Skript)