 |
Aber jetzt zum Dreh- und Angelpunkt der Bedeutung von Versetzungen für die
Menschheit. Wir werden dies in Kap. 8 noch ausführlicher
behandeln, hier geht es um das Prinzip. |
|
 |
Hier noch einmal die entscheidende Ausage: |
| |
| Plastische Verformung aller Kristalle erfolgt ausschließlich durch
die Erzeugung und Bewegung von Versetzungen |
|
 |
Die Umkehrung ist auch richtig: Will ich plastische Verfomung verhindern, muß
ich die Erzeugung und (wichtiger) die Bewegung von Versetzungen verhindern. |
|
 |
Aber nicht immer und hundertprozentig - denn sonst hätte ich ein sprödes Material
- sondern so daß ich maximale "Härte"
(=Widerstand gegen plastische Verfomrung) kombiniere mit einem Rest an Duktilität=plastische
Verformbarkeit. |
|
 |
Das Paradigma dazu
war jahrtausendelang das "magische" Schwert; heutzutage ist
es die Autokarrosserie (und der Golfschläger!). |
 |
Selbstverständlich ist plastische Verformbarkeit außerordentlich nützlich,
um ein bestimmtes Teil herzustellen (Kotflügel etc., z.B. durch Pressen). Aber auch Glas könnte man (bei höherer
Temperatur) in die Form eines Kotflügels oder Schwerts pressen; trotzdem haben Glasschwerter keine Bedeutung erlangt. |
|
 |
Denn plastische Verformbarkeit ist auch beim fertigen Produkt, das sich eigentlich nicht mehr verformen soll, eminent praktisch: Das Stahlschwert bricht eben nicht, wenn man auf
ein anderes Stahlschwert haut, sondern hat allenfalls eine kleine Macke (=lokale plastische Verformung). Schlecht, aber
allemal besser als der beim Glasschwert sichere Bruch. Bei Kotflügeln etc. gilt dasselbe Prinzip. |
 |
Plastische, d.h. bleibende Verfomung heißt, daß sich ein Kristall
nach Einwirkung einer Kraft bleibend verformt hat. Das gilt z. B. für einen Kotflügel, nachdem man gegen einen
Baum gefahren ist - der Metallkristall hat jetzt eine ander Form als vorher. Der Baum selbst, falls man ihn nicht gefällt
hat, hat sich i.d.R. elastisch verformt (von den Verletzungen der Rinde abgesehen).
Er ist nach Wegnehmen der Kraft wieder in der vorherigen Gestalt. |
|
 |
Plastische Verformung bedingt zwangsläufig, daß Teile eines Kristalls sich gegenüber
anderen Teilen verschoben haben. Einige Atome sind nicht mehr dort, wo sie früher waren. Die damit verbundenen bleibenden
Verschiebungen der Atome werden immer durch den Durchlauf von Versetzungen durch den Kristall erzeugt.
|
|
 |
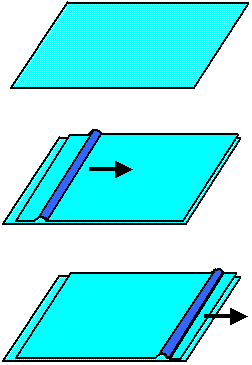
Betrachten wir z.B. Bild 2a als einen Zustand, bei dem die
durch den Schnitt definierte Versetzung von der orangefarbigen Oberfläche aus in den Kristall hineingelaufen ist, so
wäre nach weiterem Durchlaufen der Versetzung "nach hinten", der obere Teil des Kristall gegenüber dem
unteren um genau einen Burgersvektor verschoben sobald die Versetzung an der Rückseite austritt. |
|
 |
Das schauen wir uns genauer an |
|
|
|
 |
Im ersten Schritt legen wir eine "Scherspannung"
an, die den oberen Teil des Kristalls gegenüber dem unteren Teil nach links verschieben möchte. |
|
 |
Solange die Spannung nicht zu groß ist, wird der Kristall sich nur elastisch
verformen. Nach Überschreitung einer bestimmten Größe, der Fließspannung
oder Fließgrenze, bildet sich jedoch eine Stufenversetzung, die in der gezeigten Weise durch den Kristall wandert.
Auf der linken Seite hat sich eine Stufe gebildet; die Höhe der Stufe ist durch den Burgersvektor der Versetzung gegeben. |
|
 |
Nach Durchqueren des Kristalls hat sich auch auf der rechten Seite eine Stufe gebildet. Der Nettoeffekt
des Durchgangs der Versetzung ist die Abgleitung der oberen Kristallhälfte relativ zur unteren
um einen Burgersvektor. |
 |
Warum so kompliziert, wenn es eigentlich auch einfach geht? Warum rutscht die obere Kristallhälfte
nicht einfach geschlossen nach links? Die Antwort werden wir uns in Kapitel
8 noch genauer anschauen: hier nur soviel: Dazu müßten erheblich höhere Kräfte wirken - man muß
ja sehr viele Bindungen gleichzeitig lösen; mit einer Versetzung sind es viel weniger. |
 |
Im täglichen Leben ist das ein bekannter Effekt. Oft gelingt die Bewegung eines Körpers
relativ zu einem anderen viel besser, wenn ein "Defekt" erzeugt wird, der durch den Körper läuft. Nachfolgend
ohne Kommentar drei Beispiele. |
| |
 |
 |
 |
| Teppichverrücken mit Falte |
Raupe ("Inchworm") |
Wurm |
|
 |
Wie kann eine makroskopische Verformung in alle drei Raumrichtigen (Kotflügel!)
durch Versetzungen entstehen, wenn eine Versetzung gerade mal eine Verformung um Bruchteile
eines Nanometers bewirkt? Die Antwort ist klar: |
|
 |
1. Es müssen sehr viele Versetzungen zusammenwirken, und
|
|
 |
2. Sie müssen auf vielen verschiedenen Ebenen
durch den Kristall laufen. |
 |
Das wird uns in Kapitel
8 noch beschäftigen, hier wollen wir noch ein Maß für die Menge an Versetzungen in einem Kristall definieren,
die Versetzungdichte
r.
Wir nehmen dafür einfach die Gesamtlänge aller Versetzungen in einem cm3des
Kristalls, so daß gilt |
| |
| r | = |
Gesamtlänge Versetzungen
Volumen Kristall |
|
|
 |
Die Dimension von r darf einen nicht in die
Irre führen - es sind cm pro cm3! Die durch 1/cm2 insinuierte Flächendichte
hat jedoch auch einen Sinn - dazu eine Übungsaufgabe. |
|
|
| Übung
4.1-2 |
| Versetzungsdichten - Definitionen und Messung |
|
 |
Wie groß sind Versetzungsdichten in normalen Kristallen? Die Antwort mag
überraschen: man findet eine Bandbreite von 0 cm–2 bis zu 1012
cm–2! Beispiele dazu: |
|
 |
Versetzungsfreies Silizium - das Basismaterial
für die Siliziumtechnologie: r=0 cm–2
Es gibt auch noch versetzungsfreies
Ge, sonst haben alle Kristalle (mit Ausnahme mikroskopisch kleiner) immer eine endliche Versetzungsdichte. |
|
 |
"Gute" Einkristalle (fürs Labor gezüchtet):
r
» (103 - 105) cm–2. |
|
 |
Normale Kristalle inkl. Polykristalle: r
» (105 - 109) cm–2. |
|
 |
Stark verformte Kristalle:
r=bis 1012 cm–2. |
 |
Wenn man sich vor Augen hält, daß eine Versetzungsdichte von 1010
cm–2 bedeutet, daß in einem cm3 Kristall insgesamt 1010 cm=100
000 km Versetzungen stecken, wird begreiflich, warum sich selbst große makroskopische Verformungen durch die winzigen
Verschiebungen der Einzelversetzung darstellen lassen. |
 |
Zum Schluß ein Bild aus dem
Transmissionselektronenmikroskop (TEM), mit dem man bei hoher Vergrößerung durch dünne
(d.h. Dicke » 1 µm) Kristalle hindurchsehen,
und dabei Versetzungen direkt sichtbar machen kann. Die dreidimensionale Versetzungsstruktur wird dabei projeziert dargestellt. |
|
 |
Viele weitere Beispiele sowie das "Funktionsprinzip" der Elektronenmikroskopie für
diesen Fall finden sich im Link. |
| |
|
© H. Föll (MaWi 1 Skript)