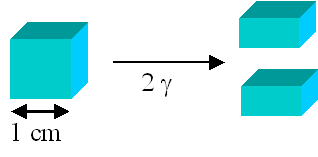|
Wir haben bereits diskutiert,
daß die Oberfläche (oder genauer die Grenzfläche
Material - Umgebung) als Kristalldefekt behandelt werden muß. Bei der Oberfläche ist leicht einsichtig, daß
sie einen eigenen Energiebeitrag in die Energiebilanz des Kristalls einbringt. Die Atome auf der Oberfläche haben andere
Bindungsverhältnisse als Atome im Inneren des Körpers, und damit auch andere energetische Bedingungen.
|
|
 |
Die Angabe einer Oberflächenenergie
g
ist sinnvoll, mit g = Energie der Oberfläche/cm2
= Energieaufwand, der benötigt wird um 1 cm2 neue Oberfläche zu schaffen. |
| |
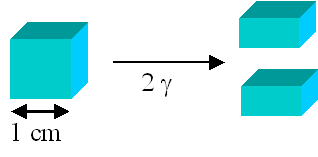 |
| Die Oberflächenenergie vergößert sich um 2g
|
|
|
 |
Typische Oberflächenenergien (nach Barett)
sind z.B.:
g(Glas) = 300 erg/cm2 = 3 00 mJ/m2
g(Fe) = 2100 erg/cm2 = 2 100 mJ/m2
(Leider werden Grenzflächenenergieen
noch gerne in den alten cgs Einheiten angegeben. Die
Unrechung auf SI Einheiten ist aber in der gezeigten
Weise einfach. Dabei ist 1 erg = 10–7
J; d.h. 1 erg/cm2 = 1 mJ/m2). |
 |
Das sind aber relativ unanschauliche Zahlen, deshalb wollen wir in einer Übungsaufgabe
ein etwas intimeres Verhältnis zu diesen Werten bekommen |
|
|
|
 |
Alle zweidimensionalen Defekte fallen unter die oben schon angedeutete Definition, die wir
jetzt verallgemeinern wollen. |
| |
|
Flächenhafte Defekte = Grenzflächen |
| |
|
 |
Jeder flächenhafte Defekt ist eine Grenzfläche
zwischen zwei Körpern; man kann dem Defekt auch immer eine Grenzflächenenergie
analog der Oberflächenenergie zuschreiben. Der Sprachgebrauch ist aber oft schlampig bzw. beschreibt komplizierte Dinge
in einem Wort, das dann eine Art Oberbegriff ist. |
|
 |
Wenn man z.B. von der Oberfläche eines Si-Kristalls
spricht, redet man von einem Gebilde, das die Grenzfläche des Siliziumkristalls
zu dem sich an Luft gebildeten etwa 2 nm dicken SiO2
und die Grenzfläche des SiO2
mit der Luft umfaßt. Eine Grenzfläche Si - O2/N2 gibt es nicht, da sofort eine Oxidation
erfolgt und sich SiO2 bildet. |
|
 |
Wohldefiniert ist dagegen die Grenzfläche Si - (Ultrahoch)vakuum. Daß die
Oberfläche ein Defekt ist, wird insbesondere bei der {111} Oberfläche in diesem Fall sehr deutlich, da
sich die Oberflächenatome völlig neu anordnen, um die Oberflächenergie zu minimieren. Mit dem Rastertunnelmikroskop
kann man das (im Link) direkt sehen: Die Anordnung hat keinerlei Ähnlichkeit
mit der {111} Ebene eines Diamantgitters. Auf anderen Ebenen treten ebenfalls solche Reorganisationen auf, aber nicht so ausgeprägt wie auf der {111} Oberfläche. |
 |
Je nach Art der sich entlang der Grenzfläche berührenden Körpern
spricht man abgesehen von der Oberfläche im wesentlichen von folgenden zweidimensionalen Defekten: |
| |
Phasengrenze:
Grenzfläche zwischen zwei verschiedenen (im Sprachgebrauch i.d.R. festen) Körpern. |
Korngrenze:
Grenzfläche zwischen identischen, aber zueinander beliebig orientierten Kristallen. |
Stapelfehler:
Grenzfläche zwischen zwei identischen und sehr speziell zueinander orientierten Kristallen. |
|
| | |
|
|
Phasengrenzen und Korngrenzen |
| |
|
 |
Phasengrenzen sind wohl die häufigsten
und für unser Zwecke sehr leicht zu verstehende Defekte. Allerdings sollten wir den Begriff "Phase"
noch definieren: |
|
 |
Unter einer Phase wollen wir
einen homogenen, unterscheidbaren und (im Prinzip)
mechanisch abtrennbaren Teil eines gegeben Materials mit gegebener chemischer Zusammensetzung
verstehen. |
 |
Phasengrenzen umfassen eine Unzahl von möglichen Grenzflächen - zum Beispiel die
Grenzfläche zwischen kristallinem und amorphen Silizium, zwischen Si und SiO2 oder Pd2Si
(Palladiumsilizid), oder .... Aber auch die Grenzflächen zwischen dem Fe - Kristall und den eingelagerten kleinen
Graphitpartikeln des Gußeisens, den Glasfasern und dem Epoxyharz der glasfaserverstärkten Kunststoffe, zwischen
den Glimmer- und Feldspatteilchen des Granits oder den Bestandteilen von Beton sind Phasengrenzen. |
|  |
Wir sind daran gewöhnt, daß die meisten Materialien des täglichen Lebens Phasengrenzen
enthalten und daß die Phasengrenzen viele Eigenschaften bestimmen. Über diese Phasengrenzen denken wir gar nicht
nach: ihre Eigenschaften sind empirisch mehr oder weniger bekannt. |
|
 |
Nicht allgemein bekannt ist, daß auch einige Hochtechnologieprodukte sehr stark von den Eigenschaften
ihre Phasengrenzen dominiert werden; darunter fallen z.B. viele optoelektronische Bauelemente oder Festkörpersensoren. Die exakte Struktur der Phasengrenzen und
insbesondere die Vermeidung bestimmter struktureller Eigenheiten in diesen Defekten ist von überragender Bedeutung
für die Produkte und Objekt großer Forschungsanstrengungen. |
 |
Zwei Bilder im Link sollen die mögliche
Komplexität von Phasengrenzen illustrieren ohne daß wir uns in Details verwickeln. Wer mehr wissen möchte;
kann einen Blick in das Hyperskript "Defects
werfen. |
 |
Die Phasengrenze zwischen zwei Kristallen identischer Bauart aber verschiedener
Orientierung, heißt Korngrenze, ihre Geometrie ist damit verständlich. Ein Schemabild
zeigt sofort, daß die einzelne Korngrenze dabei beliebige Orientierungen im Raum haben kann. |
|
 |
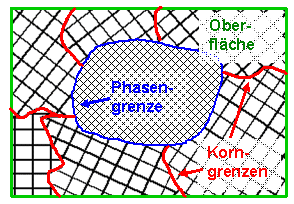
Hier eine schematische (zweidimensionale) Darstellung von Kristallkörnern in willkürlicher
Form mit den zugehörigen Korngrenzen, der Phasengrenze zu einer Ausscheidung und der Oberfläche. |
| |
|
 |
Korngrenzen sind per definitionem die (meist beherrschenden) Defekte in Polykristallen, während sie - ebenfalls per definitionem - in Einkristallen
nicht vorkommen. Fast alle natürlicherweise vorkommenden Kristalle sind Polykristalle; Einkristalle sind selten und
dann oft kostbar; man denke an die Edelsteine. |
|
 |
Künstlich hergestellte Einkristalle sind zwar nicht selten, aber trotzdem kostbar. Von
überragender Bedeutung sind die Silizium
Einkristalle, der Grundstoff der Mikroelektronik, mit einem Markt im Jahre 1999
von ca. $ 8 · 109 pro Jahr. In der Optoelektronik gilt dasselbe für GaAs und verwandte Kristalle. |
|
 |
Weiterhin werden Einkristalle aller Arten für viele Anwendungen in der Optík gebraucht.
Aber auch besonders leistungsfähige (und treibstoffsparende) Flugzeugturbinen benötigen einkristalline Schaufeln
aus einer Ti - Legierung. |
 |
Man erkennt an den Beispielen, daß Korngrenzen die Eigenschaften eines Materials
sehr stark beeinflussen können, sonst würde man sich ja nicht die Mühe machen teure Einkristalle für
technische Zwecke zu "züchten". Das heißt aber nicht, daß
Korngrenzen immer "schlechte" Defekte sind. Je nach Anwendung eines Materials können sie nützlich oder schädlich sein.
|
 |
Die atomare Struktur von Korngrenzen ist sehr kompliziert; das soll uns aber hier
nicht interessieren. Auf jeden Fall haben Korngrenzen als innere Grenzflächen eine Grenzflächen- oder Korngrenzenenergie;
sie liegt ganz grob (z.B. für Si) in der Größenordnung von 300 erg/cm2 = 300 mJ/m2. |
|
 |
Da diese Korngrenzenenenergie stark von der exakten Geometrie abhängen kann (d.h. der
relativen Orientierung der beiden Kristalle zueinander und der kristallographischen Ebenen der Korngrenze in einem der Kristalle),
und das Prinzip der Energieminimierung immer noch gilt, findet
man in realen Kristallen häufig ganz bestimmte Korngrenzen (sog. Zwillingskorngrenzen) mit besonders niedriger Energie
(z.B. ca. 50 mJ/m2 statt ca. 300 mJ/m2 im Silizium). |
|
 |
Dies führt uns zu weiteren speziellen flächenhaften Defekten, den Stapelfehlern,
die mit den Zwillingskorngrenzen eng verwandt sind. |
|
|
|
Stapelfehler |
| |
|
 |
Stapelfehler entstehen in unserer prinzipiellen Definition, wenn man zwei durch
ihre Stapelfolge definierten Kristalle entlang
einer Grenzfläche so zusammensetzt, daß beide Kristall zwar exakt gleich orientiert sind, an der Nahtstelle aber
die Stapelfolge nicht stimmt. Wir machen uns dies in einem Gedankenexperiment klar: |
|  |
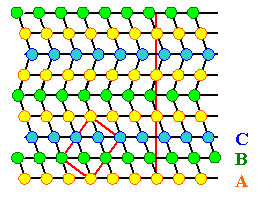
Wir betrachten den durch die Stapelfolge
ABCABCABCABC... definierten fcc - Kristall |
|
 |
Wir schneiden den Kristall auf einer der Stapelebenen in 2 Hälften und erhalten zwei Kristalle,
z.B.
|
| |
ABCABCA und BCABCABC... |
|
 |
Wir fügen die Kristalle wieder zusammen, aber so, daß die erste (= linke) Lage
des 2. Kristalls (die B-Lage in der früheren Nomenklatur) jetzt die im Kristall mögliche 2.
Alternative wahrnimmt, d.h. bezüglich der Nomenklatur im 1. Kristall zur C-Lage wird. Entsprechend wird
aus der alten C - Lage dann die A - Lage und aus der A - Lage die B - Lage. Dazu müssen
wir unseren 2. Kristall (in der Schnittebene) etwas verschieben (genau gesagt um einen Vektor
des Typs a/6<112>). |
 |
Das gleiche Ergebnis erhält man, wenn man in einem leicht modifizierten 2.
Rezept die B-Lage des 2. Kristalls gedanklich abschält und wegwirft, und die beiden Kristalle dann
ohne Verschiebung wieder zusammenführt. |
|  |
Was wir in beiden Fällen bekommen ist der Kristall |
|
| ABCABCACABCABCABC... |
 |
Dieser Kristall enthält ersichtlich einen flächenhaften Fehler, eben einen Stapelfehler. Der in der Stapelfolge gezeigte Defekt ist aber nicht der einzige möglich
Typus von Stapelfehlern. Das Rezept läßt sich auf alle Kristalle anwenden, die über das Stapeln von Ebenen
definiert werden können (und das sind letztlich alle) und außerdem noch erweitern. Wir schauen uns eine Erweiterung
für fcc Kristalle an: |
|
 |
Wir schließen an das 2. Rezept von oben an, schneiden eine Stapelfolge irgendwo auf, werfen
aber nicht die erste Ebene des 2. Kristall weg, sondern fügen eine zusätzliche Ebene ein. Das sieht für
fcc Kristalle so aus: |
|
 |
ABCABCABCABC.... + Schnitt =
ABCABC und ABCABCABC... . Ebene einfügen ergibt
ABCABC und BABCABCABC... . Nach Zusammenfügen haben wir
ABCABCBABCABC.
Da wir keine Kopf-auf-Kopf Situation zulassen, konnte nur eine B
- Ebene eingefügt werden. |
|
 |
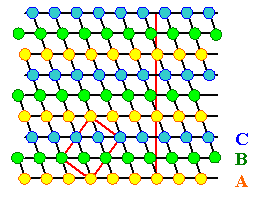
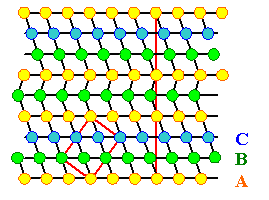
Schauen wir uns das mal an |
|
|
|
 |
Die zwei Stapelfehler unterscheiden sich deutlich; zur Unterscheidung werden sie
intrinsisch oder extrinsisch
genannt, je nachdem ob eine Ebene fehlt oder zuviel
ist |
|
 |
Diese Bezeichnung hat einen Sinn, der sich uns im nächsten Unterkapitel erschließt. |
 |
Stapelfehler scheinen etwas "künstliches" zu sein. Deshalb nehmen wir hier erstmal
nur zur Kenntnis: |
|
 |
Stapelfehler in dichtestgepackten Kristallen sind sehr prominente
Defekte, die sehr häufig auftreten und oft nur schwer zu vermeiden sind. |
|
 |
Stapelfehler und Versetzungen sind insbesondere in fcc Kristallen oft zu etwas neuem
kombiniert (einer "aufgespaltenen Versetzung"). Ohne auf Einzelheiten einzugehen,
soll doch angemerkt werden, daß die Eigenschaften der Stapelfehler damit sehr stark die Versetzungsmechanik und damit
die plastische Verformbarkeit dieser Materialien beeinflußt. |
|
 |
Ein Sorte Stapelfehler in Silizium hat sogar einen eigenen Namen und heißt "Oxidationsinduzierte Stapelfehler"
(OSF).
Wir ahnen: Diese OSFs, oder besser gesagt ihre Vermeidung, sind sehr wichtig für
die Si-Technologie, und außerdem werden sie wohl durch einen Technologieprozeß, die Oxidation, erzeugt. |
 |
Zum Schluß noch einen Überblick über die Größenordnung
von Grenzflächenenergien. Die Zahlenwerte sollten immer im Zusammenhang mit der Übungsaufgabe von oben gesehen
werden! |
| |
| Typus | Ausprägung |
g [mJ/m2] |
| Oberfläche | W
Fe
Zn | 1450
700
380 |
"Großwinkel"
Korngrenze | Cu, Al |
» 500 | | Zwillingskorngrenzen |
Spezielle Korngrenze,
sehr häufig in fcc Gittern |
» 100 .... 200 |
"Kleinwinkel"
Korngrenze |
Durch Versetzungen darstellbar |
0 ... 100 | | Stapelfehler | Al
Cu
Au
Cu + 30% Zn
18/8 Edelstahl
fcc Co bei RT
(deshalb ist es hexagonal!) | 250
100
10
7
7
<0 |
| Phasengrenzen | | |
|
| |
|
© H. Föll (MaWi 1 Skript)