 |
Die Beschreibung eines Kristalls mit Bravaisgittern und
Basis ist nun geläufig. Wir haben aber auch schon gemerkt, daß dieser Formalismus bei einfachen Kristallen
komplizierter ist als nötig. |
|
 |
Es ist manchmal einfacher, sich einen gegebenen
Kristall direkt aus Atomen oder Molekülen, die in Ebenen liegen, zu konstruieren,
und nicht über die "Gitter + Basis" Regel. |
|
 |
Dabei hat man bei einfachen Kristallen noch den Vorteil der Anschaulichkeit und, wie wir gleich
sehen werden, der direkten Einsicht in wichtige Eigenschaften, die sich aus dem Bravais-Gitter und der Basis nicht immer
so direkt erschließen. |
|
 |
Letztlich ist dies das Vorgehen mit einem "Kristallbaukasten".
Wir besorgen uns die Bauelemente und probieren, wie sie sich am besten zusammenpassen. Die Bauelemente sind dann z.B. simple
Kugeln für alle Atome die ungerichtete Bindungen haben, Kugeln mit definierten "Ärmchen" falls kovalente
Bindungen vorliegen, oder auch ganze Moleküle mit ihren noch verfügbaren Bindungsgeometrien, falls wir einen komplexen
Kristall bauen wollen. |
|
 |
Zumindest ein Nobelpreis kam auf diese
Art zustande; es ist also kein zu verachtendes Vorgehen. |
 |
Hier wollen wir aber nur die beiden einfachsten Kristalle betrachten, die man
beim "Spielen mit Kugeln" erhalten kann. Die Aufgabe ist, mit einer Kugelsorte
einen Kristall zu formen, bei dem möglichst viele Kugeln in ein gegebenes Volumen gepackt sind - in anderen Worten,
wir wollen die dichteste Kugelpackung realisieren. |
|
 |
Das ist nicht nur für Kristalle interessant; die Menschheit hat sich auch z.B. auch ausführlich
damit beschäftigt, wie man Kanonenkugeln möglichst dicht packen kann.
|
|
 |
Obwohl es in mathematischer Strenge nicht einfach ist zu beweisen, daß die Lösung,
die wir erhalten werden, die richtige ist, hat der "gesunde Menschenverstand" damit überhaupt kein Problem |
 |
Wir beginnen, indem wir zunächst unsere Kugeln auf einer Ebene zweidimensional
möglichst dicht packen. |
|
 |
Wir erhalten automatisch einen zweidimensionalen Kristall - wer's nicht glaubt soll's (experimentell)
beweisen! |
| |

|
| Dichteste Kugelpackung in der Ebene |
|
|
|
 |
Als nächstes legen wir eine neue Lagen von Kugeln auf die bereits vorhandene
Ebene. |
|
 |
Selbst wenn wir gedankenlos die Kugeln der 2. Ebene irgendwo hinlegen, würden
sie automatisch in die Kuhlen rutschen, d.h. das Zentrum einer Kugel der 2. Ebene liegt exakt im Zentrum der leicht
verbogenen projezierten Dreiecke, die zwischen den Kugeln der 1. Ebene aufgespannt werden. |
|
 |
Wir erhalten das nachfolgende Bild (die 2. Ebene ist halbtransparent gewählt). |
| |
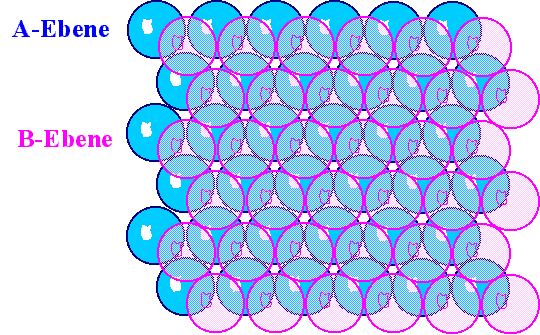 |
| Dichteste Kugelpackung mit zwei Ebenen |
|
|
 |
Um beim Übergang zu vielen aufeinanderliegenden Ebenen eine einfache Bezeichnung zu haben,
nennen wir die blaue Ebene und alle Ebenen, die bei senkrechter Projektion exakt über
der blauen Ebene liegen, A-Ebenen, die rosa Ebene und alle die exakt über
ihr liegen heißen B-Ebenen. |
 |
Das rote Atom liegt in der Projektion exakt über einem Atom der A - Ebene. Wenn wir ausgehend von diesem Atom die dritte Ebene bauen, erhalten wir also
wieder eine A - Ebene. |
 |
Das grüne Atom aber liegt weder über der A- noch über der
B - Ebene. Mit grünen Atomen erhalten wir also eine neue Ebene, die in unserer Nomenklatur konsequenterweise
C - Ebene heißt. |
 |
Daß es sich wirklich um verschiedene Ebenen handelt, wenn wir ausgehend
vom roten oder grünen Atom die Ebenen konstruieren, sieht man sofort: Die rote oder grüne Ebenen paßt nicht
zusammen; es entsteht eine Linie entlang der sich ein Passungsfehler definieren läßt. |
|
 |
Dies gibt uns eine erste Ahnung davon, was Kristallbaufehler
sind und wie sie entstehen können. |
|
 |
Denn wenn wir uns vorstellen, daß auch richtige Kristall so wachsen, daß sich
auf dichtest gepackten Ebenen Atome in die Kuhlen setzen, ist leicht vorstellbar,
daß das manchmal falsch läuft. Wenn diese falsch besetzte Lage dann wächst, wird sie mit den anderen, unabhängig
und "richtig" entstandenen Lagen nicht zusammenpassen; der Kristall enthält einen Defekt. |
| |
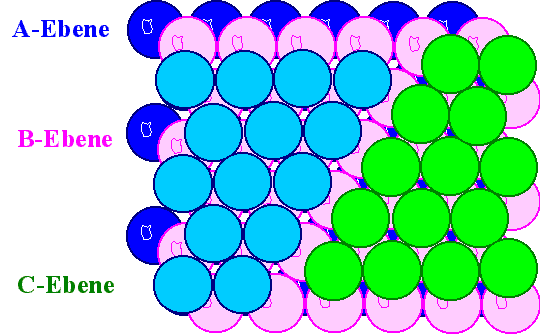
|
| Dichteste Kugelpackung mit den zwei möglichen Varianten
der dritten Ebene |
|
 |
Wir haben also zwei Möglichkeiten, einen
Kristall in dichtester Kugelpackung zu erzeugen: |
|
 |
Wir starten mit einer hexagonalen zweidimensionalen A-Ebene; darauf kommt
eine B-Ebene |
|
 |
1. Möglichkeit: Wählen wir als dritte Ebene wieder
eine A-Ebene und machen dann periodisch weiter, erhalten wir die Stapelfolge:
ABABABABA.... |
|
 |
Der Kristall den wir so erhalten, hat genau die vorher diskutierte hexagonal dichteste Kugelpackung
(hcp),das ist unmittelbar zu sehen. |
|
 |
2. Möglichkeit: Wählen wir als dritte Ebenen aber
eine C-Ebene, bekommen wir die Stapelfolge ABC. Wenn wir diese Folge dann immer wieder wiederholen,
erhalten wir
ABCABCABCABC...,
|
|
 |
- und dies ist genau das fcc Gitter wenn wir die Aufeinanderfolge der {111}
Ebenen betrachten - nur ist das nicht ganz so leicht zu sehen. |
 |
Allgemein betrachtet haben wir jetzt einen Kristall erzeugt, indem wir nicht einzelne
Atome auf durch Gitter und Basis definierte Plätze gesetzt haben, sondern ganze Ebenen von Atomen aufeinander stapeln. |
|
 |
Da dies nicht immer so direkt einsichtig ist, wollen wir dazu eine kleine Übung machen. |
| |
|
 |
Daß man mit dieser "Kristallbautechnik" nicht nur die bekannten
dichtestgepackten Strukturen machen kann, ist klar. Wir könnten aber selbst innerhalb einer dicht gepackten Struktur
noch Modifikationen einbringen: |
|
 |
Es könnte z.B. folgendermaßen aussehen
ABCBABCB ABCB... oder ABCBCABCBCABCBC
...;
jedesmal produzieren wir einen (komplizierten) Kristall mit der jeweils farbig markierten Einheit der Stapelfolge.
|
|
 |
Es ist auch nicht prinzipiell verboten, x mal, z.B. 30 mal, ABAB... zu
stapeln, und nach jedem x. Block eine C-Ebenen einzufügen:
ABAB...(30X) ... ABABCABAB...(30X)..ABC AB... |
|
 |
So etwas in der Art kommt tatsächlich vor! Die wichtige Verbindung SiC
(Siliziumcarbid) hat (aus technischer Sicht leider) viele Modifikationen mit den merkwürdigsten
Stapelfolgen! Man nennt dies ganz allgemein Polymorphismus; für den Fall dass die
diversen Morphologien sich nur in einer Dimension unterscheiden (wie hier beim Stapeln
in einer Richtung) auch Polytypismus. |
|
 |
Wir könnten auch beliebig stapeln, wobei wir nur darauf achten, daß
keine Kopf - Kopf Stapelfolge (z.B. AA) entsteht; z.B.
ABCBACBACABCABCBA...
aber da wir keine Translationssymmetrie mehr haben, ist das eigentlich kein richtiger Kristall
mehr. |
 |
Unser Spiel mit Kugeln produziert also in simpelster Weise das hexagonale Bravaisgitter
mit zwei Atomen in der Basis, das kubisch flächenzentrierte Bravaisgitter mit einem Atom in der Basis, aber auch kompliziertere
Gitter. Wir beenden dieses Unterkapitel mit einer kleinen Übung, die uns sowohl hilft, die Geometrie des fcc
- Gitters besser zu verstehen als auch - ein Kapitel später - die spezifischen Defekte dieses Gitters. |
|
|
|
|
© H. Föll (MaWi 1 Skript)
