 |
Die Elemente des Periodensystems kondensieren alle
bei genügend tiefer Temperatur (und beim He noch bei genügend hohem Druck) in feste Körper, und diese
sind fast durchweg Kristalle. Ungefähr 95% aller Elementkristalle haben dabei einen der drei folgenden Gittertypen: |
|
|
 |
Kubisch-flächenzentriertes Bravaisgitter
,
abgekürzt fcc
für "face centered cubic" oder, gelegentlich auf deutsch, kfz. Dieses Gitter besitzt eine
dichteste Kugelpackung. |
|
 |
Mit einem Atom in der Basis, das dann auf
den Ecken und Seitenmitten des Würfels sitzt, kristallieren z.B. Al, Ni, Cu, Pd, Ag,
Pt, Au sowie alle Edelgase. |
|
 |
Mit zwei Atomen in der Basis, eines bei der
Position (0,0,0) der Würfelecke, das andere dann bei (1/4, 1/4, 1/4), kristallisieren Si, Ge,
C (als Diamant) und Sn unterhalb von 13 oC. Diese Kristallsorte hat einen eigenen Namen:
Man spricht vom "Diamantgitter" – obwohl man eigentlich "Diamantstruktur" meint. |
|
 |
Etwa 30 % aller Elemente kristallisieren in einem fcc-Gitter. |
 |
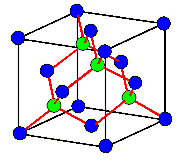
Da wir das "Diamantgitter" bisher nicht behandelt haben, wollen wir
uns diesen Kristall kurz anschauen. Zeichnet man Verbindungen zwischen den Atomen (hier rot),
erkennt man sofort die typische Symmetrie der sp3-Hybridorbitalbindungen. |
|
 |
Bei den Elementkristallen sind natürlich alle unten gezeigten Kugeln
Atome derselben Sorte. Wir bekommen denselben Kristalltyp aber auch bei vielen technisch wichtigen Halbleitern, wenn wir
zum Beispiel die grünen oder blauen Kugeln als Ga oder In, und die jeweils anderen als As, P
oder Sb betrachten. |
|
 |
Richtige Rohdiamanten sind im Link gezeigt. |
| |
 |
 |
 |
fcc-Bravaisgitter
(blaue "Punkte") |
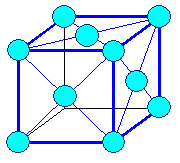
fcc-Elementkristall
(blaue "Atome") |
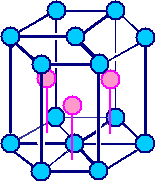
Kristall mit Diamantstruktur
(dunkelblaue und grüne "Atome") |
| Ein letztes Mal sei auf den Unterschied zwischen Gitter
und Kristall hingewisen, der in symbolischen Zeichnungen oft verschwindet. |
|
| |
|
|
 |
Wie immer symbolisieren die Kugeln Atome, aber mit viel zu kleinen
Durchmessern. Würde man die Durchmesser maßstabsgetreu zeichnen, ist nicht mehr viel zu erkennen. |
 |
Die Zahlenwerte der Gitterkonstanten
einiger Kristalle sind im Link gezeigt. |
|
|
 |
Kubisch-raumzentriertes Bravaisgitter,
abgekürzt
bcc für
"body centered cubic" oder, gelegentlich auf deutsch, krz.
|
|
 |
Mit einem Atom in der Basis, das dann auf
den Ecken und im Zentrum des Würfels sitzt, kristallieren z.B. K, Rb, Cs, V, Nb,
Ta, Cr, Mo und W. |
|
 |
Etwa 30 % aller Elemente kristallisieren in einem bcc-Gitter |
| |
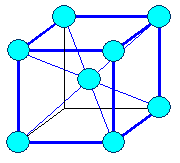 |
bcc-Bravaisgitter
oder bcc-Elementkristall |
|
 |
Hexagonales Bravaisgitter und Hexagonal dichteste Kugelpackung,
abgekürzt hex bzw.
hcp
für "hexagonal close packed". |
|
 |
Die hexagonal dichteste Kugelpackung entsteht, wenn man
ein hexagonales Bravais-Gitter mit einer Basis aus (mindestens) zwei
gleichartigen Atomen kombiniert. Das erste Atom sitzt bei (0,0,0), das zweite bei (1/2, 1/4, 1/2); also auf
halber c-Achsenhöhe im Zentrum eines Basisdreiecks. Es gibt also kein hexagonal dichtest gepacktes Gitter, sondern immer nur einen hexagonal dichtest gepackten Kristall. |
|
 |
Daß mit dieser Anordnung eine dichteste
Kugelpackung entsteht, d.h. dass es keine Möglichkeit gibt, mehr (gleichgroße) Kugeln in ein gleichgroßes
Volumen zu packen, werden wir weiter unten sehen. |
|
 |
Etwa 35 % aller Elemente kristallisieren in einem hcp-Kristall, darunter beispielsweise
Mg, Re, Co, Zn, Cd, C (als Graphit), aber auch z.B. N bei tiefer Temperatur. |
 |
Da wir die hexagonal dichteste Kugelpackung
bisher nicht behandelt haben, wollen wir uns jetzt einen auf derartigen Kristall kurz
anschauen |
| |
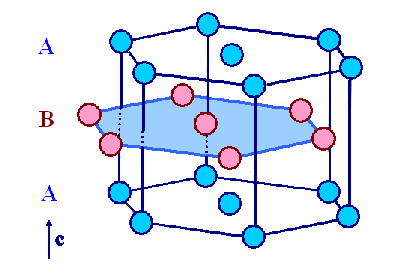 |
Hexagonales Gitter (blaue "Punkte") und
hexagonal dichtest gepacktes Gitter (blaue und rote Atome) |
|
 |
In diesen drei Gittertypen (oder Kristalltypen) kristallisieren ca. 95% der Elemente. Wir sehen auch, daß es zunehmend
(sprachlich) schwer fällt, die saubere Unterscheidung zwischen Gitter und Kristall aufrechtzuerhalten, und wundern
uns nicht mehr über gelegentliche Unsauberkeiten. |
|
 |
Je nach Element wird immer diejenige Kristallstruktur gewählt, die am besten
zu den Bindungsverhältnissen paßt, d.h. die größte Energieabsenkung
zur Folge hat. |
|
 |
Viele Elemente kommen aber in mehreren Kristallstrukturen
vor - z.B. der Kohlenstoff, der, wie wir wissen, in der Regel als Graphit (hex-Gitter) und nur selten als Diamant
(fcc-Gitter) vorliegt. Bei gegebenem Druck und Temperatur kann allerdings immer nur ein
Gitter stabil, d.h. energetisch am günstigsten sein. Diamant ist bei Raumtemperatur und Normaldruck eigentlich nicht
stabil sondern nur metastabil; glücklicherweise dauert aber die Umwandlung
zum stabilen Graphit bei Raumtemperatur nahezu unendlich lange. |
 |
Bei anderen Elementen, oder ganz allgemein, bei beliebigen
Kristallen, ist das aber nicht immer so. |
|
 |
Bei bestimmten Temperaturen und Drücken erfolgt eine spontane Umwandlung
in ein anderes, bei diesen Zustandgrößen stabiles und nicht nur metastabiles Gitter.
|
|
 |
Eisen (Fe), unser wichtigstes Metall, erstarrt unterhalb des Schmelzpunktes
von 1536 oC in ein bcc-Gitter, das sich aber unterhalb von 1402 oC in ein fcc-Gitter
umwandelt. Unterhalb von 723 oC nimmt es wieder die bcc-Gitterstruktur an. In unserem Periodensystem sind diese möglichen Modifikationen eingetragen. |
|
 |
Das ist hier noch ein bißchen rätselhaft: Eigentlich kann nur ein Gittertyp bei gegebenen Bindungspotentialen die kleinstmögliche Energie
haben. Wie schon zuvor bemerkt, laufen wir mit dem Prinzip der
Minimierung der Energie in Probleme, die sich erst im Kapitel
5 lösen werden. |
 |
Wir können am Beispiel dieser einfachen Gitter noch einige allgemeine Größen
und Zusammenhänge definieren bzw. aufzeigen, die wichtig sind und oft vorkommen. |
|
 |
Die Koordinationszahl
KZ gibt die Zahl der nächsten Nachbarn an. |
|
 |
Die Beziehung zwischen den Gitterkonstanten und den Atom- (oder Ionen-)Durchmessern.
Dazu müssen wir wissen, in welcher Gitterrichtung sich die Atome berühren, was wiederum aus der Geometrie folgt. |
|
 |
Die Zahl der Gitterpunkte in einer (Bravais)- Elementarzelle. |
|
 |
Die Packungsdichte
PD ist dann das
Verhältnis zwischen dem in einer Elementarzelle enthaltenen Volumen der Atome (immer als Kugeln gedacht; nur Teile
der Kugel mögen zählen) und dem Volumen der Elementarzelle. Damit ist dann auch die Dichte
berechenbar. |
 |
Schauen wir uns das erstmal für die obigen Kristalle an. Einige der verwendeten
Zahlen und Beziehungen ergeben sich aus der nachfolgenden Übung. |
| |
| Gittertyp |
 fcc fcc |
 bcc bcc |
 hcp hcp |
Basis-
vektoren |
a = b = c = Gitterkonstante
mit r = Atomradius | a = b = c = Gitterkonstante
mit r = Atomradius | a = b
c/a = 1,633 |
| KZ | 12 |
8 | 12 |
Atome
pro EZ |
4
(8 Eckpunkte zu 1/8;
6 Flächenpunkte zu 1/2, d.h.
8 · 1/8 + 6 · 1/2 = 4 |
2
(8 · 1/8 + 1 · 1 = 2) |
2
(8 · 1/8 + 1 · 1 = 2) |
| Für 1-atomige Basis |
| PD |
(für 1-atomige Basis) | 0,68
(für 1-atomige Basis) |
0,74 |
|
 |
Aus Packungsdichte, Gitterkonstante und Atomgewicht folgt natürlich sofort
das spezifische Gewicht des Kristalls. |
|
 |
Wir müssen üben! |
|
|
| Übung
3.3-1 |
| Ein bißchen Geometrie zu den wichtigen Gittern |
|
| |
|
© H. Föll (MaWi 1 Skript)





