5.3 Der 2. Hauptsatz der Thermodynamik

5.3.1 Entropie, freie Energie und freie Enthalpie

Makrozustände, Wahrscheinlichkeit eines Makrozustandes und Entropie

	Der erste Hauptsatz verlangt nur, daß die Energie eines Systems ohne Einwirkung von außen konstant bleibt. Er macht aber keine Aussage darüber, welcher von vielen möglichen Zuständen, die alle dieselbe Energie haben, wirklich vorliegt, d. h. welcher Zustand der wahrscheinlichste ist (Siehe auch Thermodynamik-Skript).
		Wir haben wieder das Wort "Zustand" - wir hatten es schon einmal als: "Der Zustand beschreibt die eine spezifische Lösung (der Schrödingergleichung) von den vielen möglichen, die beim betrachteten Elektron greift".
		Hier ist das nicht ganz so griffig zu definieren, aber im Grunde ist es dasselbe: Ein Zustand des Systems ist eine der möglichen konkreten Ausformungen des Systems, die mit den Randbedingungen verträglich ist.
		Das läßt sich aber noch etwas schärfer fassen und differenzieren:
	Jeden denkbaren Zustand, der durch dieselben statistischen Werte für das Gesamtsystem beschrieben werden kann - z.B. durch ein und dieselbe innere Energie, dieselbe Temperatur oder dieselbe Dichte - nennen wir einen Makrozustand. Später lernen wir dann noch den Mikrozustand kennen.
		Zwei einfache Beispiele dazu:
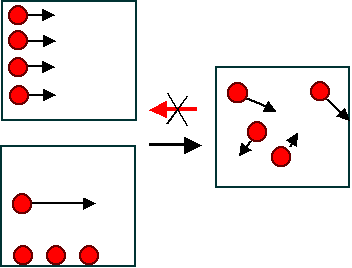
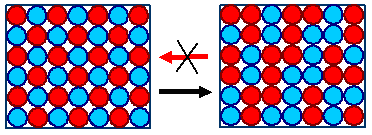
	Drei mögliche Makrozustände mit derselben kinetische Energie in einem Gas Zwei mögliche Makrozustände mit derselben Bindungsenergie in einem zweiatomigen Kristall mit identischen Bindungsenergien zwischen allen Atomen Die beiden linken Makrozustände, in der alle vier (oder in einer etwas komplexeren Zeichnung alle ca. 1024) Gasmoleküle mit gleicher Geschwindigkeit parallel fliegen, oder sich nur ein Molekül bewegt, können alle dieselbe Energie haben wie der rechte Makrozustand - aber sie sind offenkundig unwahrscheinlich. Der linke Kristall aus zwei Atomsorten ist in perfekter Ordnung. Falls die Bindungskräfte zwischen den beiden Atomsorten wie vorausgesetzt gleich groß sind, ist dies wohl ein sehr unwahrscheinlich Zustand. Wahrscheinlich ist offensichtlich der rechte Zustand. Auch wenn man mit einem unwahrscheinlichen Zustand startet, wird nach kurzer Zeit der rechte Zustand vorliegen: Die ungeordnete Bewegung aller Moleküle. Daß aus einem solchen Zustand von selbst einer der ordentlichen rechten Zustände entsteht, ist sehr unwahrscheinlich. Wahrscheinlich ist der rechte Zustand der zufälligenVerteilung der Atome. Falls die Bindungkräfte aber verschieden sind, ist die Sache nicht so einfach. Dann kann auch mal der ordentliche Zustand der wahrscheinlichere sein.

	Wieviele Beispiele man sich auch anschaut, die eher unordentlichen, chaotischen Zustände sind meist die wahrscheinlicheren - besonders bei höherer Temperatur. Um aus vielen denkbaren Makrozuständen den wahrscheinlichsten auswählen zu können, brauchen wir ein neues Axiom oder Naturgesetz; der 1. Hauptsatz ist dazu offenbar nicht ausreichend.
		Als Maß für die Wahrscheinlichkeit des Auftretens eines Makrozustandes zur selben Energie (= Temperatur) definieren wir eine neue fundamentale Größe, die Entropie S des Zustands.
		Das Wort "Entropie" stammt von Clausius, er hat es aus dem Altgriechischen komponiert mit der Bedeutung "Verwandlung, Transformation, Wendung, Änderung".
		Der wahrscheinlichste Makrozustand, die wahrscheinlichste Konfiguration, oder schlicht der Zustand, den wir tatsächlich finden wenn wir nachschauen, ist dann per definitionem derjenige Makrozustand, der die größte Entropie hat, die unter Beachtung der Randbedingungen (z.B konstante Temperatur) möglich ist.
		Der wahrscheinlichste Makrozustand ist, bezogen auf unsere Beispiele, auch der unordentlichste Zustand. Wir vermuten damit schon, daß die Entropie auch ein Maß für den Ordnungsgrad eines Zustands ist und postulieren:
		Je unordentlicher ein Zustand, desto größer ist seine Entropie
	Auch ohne zu wissen, wie Entropie in Formeln, d. h. in meßbaren Parametern definiert ist, können wir damit doch schon eine erste (qualitative) Fassung des 2. Hauptsatzes präsentieren:
		Im thermodynamischen Gleichgewicht hat ein System eine möglichst große Entropie und Die Entropie eines abgeschlossenen Systems wird nie von alleine kleiner

	Der erste Satz ist klar, der zweite Satz hat es in sich und muß erklärt werden.
		Der 2. Hauptsatz definiert irreversible Prozesse: Denn ein Prozeß, bei dem die Entropie zunimmt kann offenbar geschehen, der Rückwärtsprozeß jedoch nicht (siehe obige Gasbilder). Die Konsequenz daraus ist:
		Der 2. Hauptsatz definiert eine Richtung der Zeitachse: Auf der Zeitachse kann man sich nur in Richtung höherer Entropie bewegen. Der 2. Hauptsatz ist im übrigen das einzige Naturgesetz oder Axiom, das eine Zeitrichtung kennt. Wenn man bedenkt, wie fundamental es für uns ist, daß die Zeit immer nur in eine Richtung fließt, ist das schon sehr erstaunlich!
		Der 2. Hauptsatz definiert den Wärmetod des Universums: Irgendwann wird universelles Gleichgewicht im wahrsten Sinne des Wortes, und damit maximale Unordnung erreicht sein. Nichts wird sich mehr ändern - das Universum hat den Wärmetod erlitten.
	Wir haben nun eine neue Bedingung um Gleichgewichte zu bestimmen. Nach wie vor gilt, daß die Energie, also die innere Energie U oder die Enthalpie H, minimal sein sollte - unser altes Prinzip aus der klassischen Mechanik des Massenpunkts. Aber für viele Massenpunkte - für Materialien - gilt gleichzeitig, daß die Entropie S des Systems maximal sein soll.
		Das ist eine komplizierte Bedingung, denn eine Verkleinerung von U kann durchaus eine Verkleinerung von S zur Folge haben; man kann also beide Bedingungen i.d.R. nicht unabhängig voneinander erfüllen.
		Um beiden Bedingungen gleichzeitig zu erfüllen, definiert man am besten zwei neue Funktion, die Energie bzw. Enthalpie und Entropie eines Zustandes so verknüpfen, daß diese neuen Funktionen für die bestmögliche Kombination von U (bzw. H) und S ein Minimum haben .
	Diese neuen Funktionen beschreiben damit den Zustand, d.h. den wirklich realisierten Makrozustand aus der Menge der vielen möglichen Makrozustände des Systems; sie sind Zustandsfunktionen. Wir wollen diesen neuen Zustandsfunktionen folgende Namen geben:
		Die freie Energie F verknüpft U und S Die freie Enthalpie G verknüpft H und S
	Aus historischen Gründen heißt die freie Energie auch Helmholtz Energie, nach Hermann von Helmholtz, einem der großen Thermodynamiker und Physiker des 19. Jahrhunderts; die freie Enthalpie heißt auch Gibbsche Energie, nach Gibbs, einem berühmten amerikanischen Physiker.

	Freie Energie und freie Enthalpie
	Die Thermodynamik - in der klasssischen phänomenologischen oder in der statistischen Form - lehrt wie man zu sinnvollen Definitionen der freien Energie und Enthalpie kommt. Im Link wird darauf eingegangen, hier machen wir uns die Sache einfach und überlegen qualitativ, wie man diese Funktionen sinnvoll definieren könnte.
		Ein erster naheliegender, aber (falscher!) Ansatz wäre z.B.:
		falsch F   =  U  –  S falsch
		Zunächst sieht das nicht so schlecht aus: F wird, wie gefordert, minimal falls U möglichst klein und S möglichst groß ist.
	Aber nach kürzerem oder längerem Nachdenken kommt man unweigerlich zu dem Schluß: Hier fehlt noch was, nämlich die Temperatur T.
		Wir wissen nämlich, daß mit fallender Temperatur die Tendenz für Ordnung zunimmt - auch wenn wir das bislang nicht angesprochen haben!
	Es genügt vollständig, sich ein x-beliebiges Material vorzustellen, und zu überlegen was mit seinem Zustand passiert wenn man die Temperatur ändert; z.B. von hohen Temperaturen herkommend abkühlt.
		Aus einem unordentlichen Gas wird eine Flüßigkeit, dann ein Festkörper; i. d. R. ein Kristall. Eine Flüßigkeit ist aber ordentlicher als ein Gas; ein (perfekter) Kristall hätte perfekte Ordnung; und selbst ein Realkristall ist ja wohl ein viel ordentlicheres System von Atomen als ein Gas.
		Es gilt ganz allgemein: Mit abnehmender Temperatur steigt die Tendenz für Ordnung, mit zunehmender Temperatur steigt die Tendenz für Unordnung; und das müssen wir berücksichtigen!
	Offenbar spielt der Grad an Unordnung, d. h. der Zahlenwert der Entropie, bei tiefen Temperaturen keine so große Rolle mehr, während die Minimierung der Energie bei allen Temperaturen gleich wichtig ist: Heiße und kalte Objekte fallen z.B. immer gleichschnell nach "unten".
		Wir müssen die Entropie also mit einem Faktor gewichten, der mit der Temperatur ansteigt. Am einfachsten ist es, schlicht die Temperatur selbst zu nehmen, also T · S statt nur S.  Damit kommen wir zur richtigen Definition der freien Energie und Enthalpie:
		F  =  U  –  T · S G  =  H  –  T · S

	Das sind unsere gesuchten Zustandsfunktionen, aber sie sind mehr als das: Es sind die thermodynamischen Potentiale, die wir bei Betrachtung des chemischen Gleichgewichts postuliert haben.
		Nebenbei bekommen wir die Dimension der Entropie. Da T · S eine Energie sein muß, haben wir [S] = J · K–1.
	Damit haben wir vollständig allgemeine Bedingungen für thermodynamisches Gleichgewicht, die darüberhinaus noch extrem einfach sind (gegeben die überaus komplexe Fragestellung!!). Wir unterscheiden aus Bequemlichkeitsgründen wie zuvor die beiden Fälle mit konstantem Volumen bzw. konstantem Druck. Wir bekommen folgende Aussagen:
	Spontane Vorgänge können dann, und nur dann ablaufen, wenn sich bei konstantem Volumen und gegebener Temperatur die freie Energie F verkleinert; bei konstantem Druck und gegebener Temperatur ist es die freie Enthalpie G. Es gilt also für spontane Vorgänge bei konstantem Volumen bzw. Druck:
		dF  £  0 dG  £  0
		Nach Atkins sind das die wichtigsten Gleichungen der (physikalischen) Chemie, und damit sind sie auch für die Materialwissenschaft von überragender Bedeutung.
		Spontane Vorgänge sind Vorgänge, die von alleine, ohne äußeres Zutun ablaufen; damit sind gleichsam per definitionem Vorgänge oder Reaktionen, die in Richtung thermodynamisches Gleichgewicht führen.
	Thermodynamisches Gleichgewicht ist dann erreicht, wenn ein Zustand mit dF = 0 bzw. dH = 0 erreicht ist, und zwar bezüglich aller Variablen des Systems.
		Wie das "funktioniert" sieht man sofort, wenn wir nun unser altes Beispiel von Salz inWasser neu betrachten.
		Da H bei der Auflösung von Kochsalz von den Teilchenzahlen abhängt, z.B. von der Konzentration der Na+ und Cl– Ionen (nNa und nCl), muß für das chemische Gleichgewicht bei konst. Druck gelten:
		dGchem  =   ¶G ¶nNa · dnNa  +  ¶G ¶nCl · dnCl  +  ¶G ¶nNaCl · dnNaCl  =  0
		Für komplettes thermodynamisches Gleichgewicht bräuchten wir noch die partiellen Ableitungen nach allen andere Variablen, z.B. (¶G/ ¶T) · dT. Wir können aber im Gedankenversuch alle "uninteressanten" Variablen (oder "verallgemeinerte Koordinaten") von G konstant halten, sie tauchen dann in dG nicht mehr auf. Allerdings muß man aufpassen, denn selbst im Gedankenversuch kann man nicht immer alles konstant halten was man nicht mag!
		Ein Wort zur Nomenklatur: dF bezeichnet das totale Differential von F; ¶F/¶(...) die partielle Ableitung nach einer Variablen. Zwischen totalen Differentialen und Potentialen besteht ein enger mathematischer Zusammenhang; dies ist im obigen Link näher ausgeführt.
	Die partiellen Ableitungen sind meßbare Gößen und damit könnte man die Gleichgewichtskonzentrationen ausrechnen - aber wir müssen noch etwas aufpassen: Unsere Variabeln sind nicht automatisch unabhängig!
		Geht eine kleine Menge (dnNa) der Na Ionen in Lösung, wird eine gleichgroße Menge (dnCl = dnNa) an Cl Ionen ebenfalls in Lösung gehen müssen, sie können nicht anders. Gleichzeitig wird der NaCl Anteil, d.h.dnNaCl, um den gleichen Betrag kleiner; wir haben
		NaCl  Û  Na+  + Cl–     dnNaCl  =  –  dnNa  =  –  dnCl
	Denn die Teilchenzahlen in einem geschlossenen System sind nicht unabhängig voneinander.
		In unserem Beispiel muß immer ein Na+ und ein Cl– Ion in Lösung gehen (sonst würde der verbleibende Kristall sich elektrisch aufladen), dafür gibt es dann aber ein NaCl Molekül weniger.
		Eine allgemeine Beziehung zwischen den Teilchenzahlen läßt sich zwar formulieren, ist aber etwas trickreich, wenn man alle Arten von Reaktionen zuläßt. Für die Atome hätten wir zwar immer Si dni = 0, da sich die Zahl der Atome nicht ändert, das gilt aber nicht wenn wir als Teilchen Atome und/oder Moleküle zulassen, wie sich schon aus obigem einfachen Beispiel ergibt.
		An dieser Stelle müssen wir das aber gar nicht so genau wissen, sondern nur zur Kenntnis nehmen, dass aus der Reaktionsgleichung noch eine wie auch immer geartete Gleichung für die dni resultiert. Wer's genau wissen will, betätigt den Link.
	Damit haben wir als Gleichgewichtsbedingung für das chemische oder Teilchengleichgewicht zwei gekoppelte Gleichungen
		Si ¶G ¶ni  · dni  =  0 dnNaCl  =  –  dnNa  =  –  dnCl
	Wir werden auf diese Formeln noch zurückkommen; sie führen im übrigen direkt zum (hoffentlich) allseits bekannten Massenwirkungsgsesetz der "Chemie".
		In Prosa sagen obige Gleichungen genau das, was wir im Unterkapitel 5.3 für das chemische Gleichgewicht postuliert hatten:
		"GG liegt dann vor, wenn es "uns" (den Na+ Ionen) egal ist, ob wir im Wasser gelöst sind oder noch zum Kristall gehören, denn dann werden im Mittel genausoviel Na+ Ionen in Lösung gehen wie sich wieder abscheiden - die mittlere Zahl der gelösten und im Kristall gebunden Ionen bleibt konstant"
		In anderen Worten: Fügt man zu einem System, das chemisches Gleichgewicht erreicht hat, bei konstantem Volumen oder Druck eine infinitesimale Menge Teilchen (dn) zu, ändert sich seine freie Energie bzw. Enthalpie nicht, denn falls chemisches Gleichgewicht vorliegt gilt
		dF   =   Si ¶F ¶ni  · dni  =  0 dG   =   Si ¶G ¶ni  · dni  =  0
		Damit können wir auch das schon angesprochene chemische Potential etwas genauer definieren:
	Das chemische Potential eines Teilchens in einem gegebenen System (üblicherweise abgekürzt mit µ) ist die partielle Ableitung der freien Enthalpie (bei konst. Druck) oder der freien Energie (bei konst. Temperatur) nach der Teilchenzahl (oder Konzentration) des betrachteten Teilchens
		µi | p = const  =  ¶G ¶ni µi | V = const  =  ¶F ¶ni [µ ]  =  Energie = eV
		Im chemischen Gleichgewicht muß das chemische Potential eines Teilchen überall gleich groß sein (aber nicht unbedingt = Null!) und dG ist bezüglich Änderungen der Teilchenzahlen = Null.
	Ein Wort zum Verständnis der Nomenklatur:
		Man nennt m chemisches Potential, obwohl chemisches Gleichgewicht nicht ein Minimum der einzelnen chemischen Potentiale bedingt (wie beim mechanischen Gleichgewicht), sondern nur eine Art "Kräftegleichgewicht", d.h.
		Si ¶G ¶ni  · dni  =  S mi · dni  =  0
		Das chemische Potential ist damit eine Art Gewichtsfaktor auf der Balkenwaage der freien Enthalpie: Falls die Summe der chemischen Potentiale der Ausgangsstoffe (z.B. NaCl) gleich der Summe der chem. Potentiale der gebildeten Stoffe (Na+ und Cl–) ist, ist die "Waage" im Gleichgewicht. Ein Begriff wie "Teilchenzahlfaktor" oder "Teilchenkraft" wäre eigentlich besser. Aber es heißt nun mal "chemisches Potential" (es hat ja auch die Einheit einer Energie, nämlich eV), und wir müssen damit leben. Sehr viel mehr dazu im Link zum Hyperscript "Defects".
		Das eigentliche Potential, dessen Minimum Gleichgewicht bedingt, ist die freie Enthalpie bzw. Energie. Diese Zustandsfunktionen heißen deshalb auch thermodynamische Potentiale.

	Erstes Beispiel zum Umgang mit freier Enthalpie
	Betrachten wir ein erstes, rein qualitatives Beispiel für die großen Möglichkeiten, die im Arbeiten mit freien Energien bzw. Enthalpien stecken. Wir vergleichen die freien Enthalpien eines beliebigen Materials im festem und flüssigem Zustand, wobei wir zunächst mal annehmen, daß beide Zustände bei allen Temperaturen existieren könnten.
		Wir haben konstanten Druck, die richtige Zustandfunktion ist also die freie Enthalpie H. Die einzige Variable, die wir zulassen, ist die Temperatur T, wir haben also G = G(T).
		In beiden Zuständen oder Phasen ist der Faktor T · S = 0 für T = 0. Da die Flüßigkeit aber der unordentlichere Zustand ist, hat sie bei jeder endlichen Temperatur eine größere Entropie als der feste Zustand; T · S wird von 0 beginnend für die Flüssigkeit also schneller anwachsen müssen als für den festen Zustand.
		Die innere Energie U, oder besser die Enthalpie H, ist im flüssigen Zustand ebenfalls immer größer als im festen Zustand (Bindungen sind nicht abgesättigt; die Teilchen haben kinetische Energie); in beiden Fällen wächst H irgendwie mit T. (Nicht vergessen: T ist ein Maß für die im System steckende Energie!).
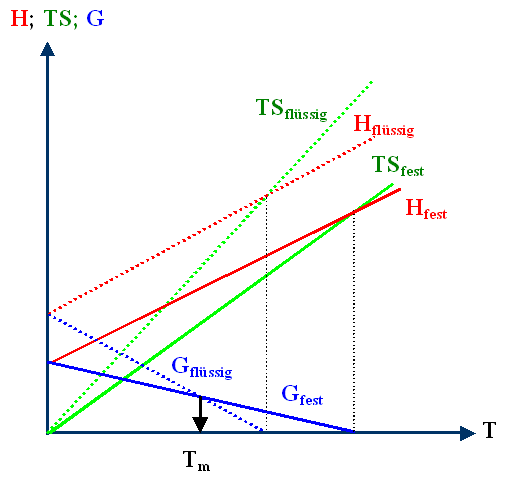
	Man erhält also folgendes prinzipielles Diagramm (die blauen Kurven sind die beiden freien Energien Gfest und Gflüssig.

	Der Einfachheit halber sind alle Kurven als Geraden gezeichnet und Schnittpunkte für H(T) und T · S(T) eingezeichnet (damit kennt man die Nullpunkte von G(T); angedeutet mit den gestrichelten Hilfslinien) und kann die G-Geraden leicht zeichnen.
		Das ist aber völlig irrelevant und vereinfacht nur die Schemazeichnung. Die Schlußfolgerung aus diesem Diagramm gilt für alle monoton ansteigenden Funktionen, ob mit oder ohne Schnittpunkte:
	Es existiert (fast) immer eine Temperatur Tm, die Schmelzpunktstemperatur, oberhalb der die freie Enthalpie Gflüssig der flüssigen Phase kleiner ist als Gfest der festen Phase. Anders ausgedrückt:
		Materialien schmelzen bzw. gefrieren, weil in der jeweilig stabilen Phase die freie Enthalpie im Vergleich zur Alternative am kleinsten ist. Das ist eine ziemlich weitreichende Vorhersage, die wir hier zwanglos erhalten!
	Wir können noch mehr erahnen: Falls die beiden G(T) Kurven sich so flach oder noch flacher schneiden, als in der Zeichnung angedeutet, wird die quantitative Berechnung von Schmelzpunkten sehr schwierig sein. Denn die Lage des Schnittpunkts zweier sich flach schneidender Geraden wird sehr stark davon abhängen, wie genau man die Geraden kennt.
		Das ist in der Tat so; Schmelzpunkte ergeben sich aus dem Vorzeichen der Differenz großer Zahlen. Kleinste Änderungen haben große Effekte, und die Berechnung von Schmelzpunkten aus Daten der Atome des Materials ist nach wie vor schwierig und unbefriedigend.

	Das Beispiel zeigt schon, daß wir das Minimierungsprinzip der freien Energie oder Enthalpie tatsächlich so interpretieren können, daß eine möglichst kleine Energie bei möglichst großer Entropie angestrebt wird.
		Wir erkennen auch, daß mit den thermodynamischen Potentialen weitreichende allgemeine Schlußfolgerungen möglich sind, ohne daß wir diese Potentiale genau kennen.
	Wir wollen mit dem 2. Hauptsatz und den darauf beruhenden Zustandsfunktionen freie Energie und freie Enthalpie aber auch quantitativ rechnen!
		Dazu müssen wir aber wissen, wie Entropie definiert ist, wie sie gemessen wird, wie sie mit einer Formel, ausgedrückt in meßbaren Größen des Systems, berechnet werden kann. Dies wird im nächsten Unterkapitels behandelt.
		Fragebogen Multiple Choice Fragen zu 5.3.1

© H. Föll (MaWi 1 Skript)