 |
Die Schrödingergleichung für das Wasserstoffatom
zu lösen ist nicht ganz einfach, aber auch nichts besonderes. Auszurechnen was passiert, wenn man in eine Flöte
bläst, ist erheblich komplizierter. |
|
 |
Aber man muß doch tief in die Systematik der Lösung von partiellen Differentialgleichungen
eintauchen, Kugelkoordinaten bemühen; Reihenentwicklungen vornehmen - eben das Instrumentarium der höheren Mathematik
anwenden. Das braucht erheblichen Platz für lange Formeln, und erheblichen Zeitaufwand um die Lösungsermittlung
abzuspulen. Wir wollen das hier nicht tun; ein Kurzabriß der Lösung
findet sich in einem "advanced" Modul (siehe auch Quantenmechanik
Skript). |
 |
Was aus der "mathematischen Übung" herauskommt (es wird so gut
wie keine Physik mehr benötigt!), sind vollständige Lösungen der Gleichung |
| |
| – |
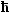 2 2
2m |
æ
ç
è |
¶2y(x,y,z)
¶x2 | + |
¶2y(x,y,z)
¶y2 | + |
¶2y(x,y,z)
¶z2 |
ö
÷
ø | + |
æ
ç
è |
e2
4pe0r |
– E |
ö
÷
ø |
· y(x,y,z) = 0 |
mit r = (x2 + y2 + z2)1/2 |
|
|
 |
Und nur auf die Lösungen yn,l,m,s(x,y,z)
wollen wir uns jetzt konzentrieren. |
|
 |
Wir betrachten zunächst die einfachsten Wellenfunktionen,
man erhält sie für die "s-Zustände", d.h. für die Kombinationen
n = 1,2,3,.. und l = s, d.h. l = 0 für alle n. Die magnetische Quantenzahl m ist
dann automatisch auch = 0. |
 |
Die entsprechende Lösung ist kugelsymmetrisch,
d.h. ihr Wert ist nur vom Abstand r des Punktes (x,y,z) vom Nullpunkt abhängig. Die zugehörigen
Energien E sind exakt die Energien aus dem Bohrschen Atommodell!
|
|
 |
Wir erhalten folgende Funktionen, denen gemeinsam ist, daß
sie mit wachsendem r gegen Null streben. |
|
|
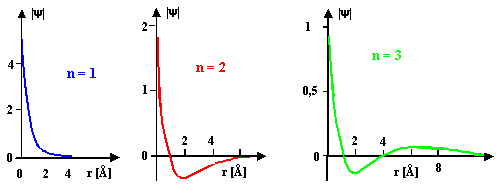 |
Radialwellenfunktionen
y von Wasserstoff für n = 1, 2, 3.
Die r - Skala gilt für
alle Graphiken;
in was für Einheiten y aufgetragen ist spielt hier noch keine
Rolle. |
|
 |
Wenn wir nun die Aufenthaltswahrscheinlichkeit
für ein Elektron in einem Volumenelement dV graphisch darstellen, also y·y* multipliziert mit dem differentiellen Volumen dxdydz, erhalten wir
für die s-Zustände, also für alle Lösungen der Schrödingergleichung
für die l = 0 ist, ebenfalls radialsymmetrische Funktionen.
|
|  |
Radialsymmetrisch heißt, daß
der Wert von y nur von r abhängt, und damit nur vom Wert des Potentials am Abstand r vom Atomkern. |
|
 |
Es empfiehlt sich dann natürlich, nicht nach der
Wahrscheinlichkeit zu fragen, das Elektron in einem Würfelchen mit Kantenlänge
dx zu finden, sondern nach der Wahrscheinlichkeit, es in der Kugelschale zwischen den Radien r und r + dr, also in einem
bestimmten Abstandsintervall, zu finden. Wegen der Radialsymmetrie ist das unabhängig
vom genauen Ort auf der Kugelschale. |
|
 |
Damit wird das Volumenelement dV proportional zu
r2dr (genau ist es 4pr2dr) und
die Aufenthaltswahrscheinlichkeit in diesem dV ist proportional zu y ·
y* · r2 · dr. |
 |
In einer dreidimensionalen Darstellung ist das "s-Elektron",
das durch diese Wellenfunktionen beschrieben wird, radialsymmetrisch um den Nullpunkt, d.h. den Ort des Atomkerns "verschmiert". |
|
 |
Dieses "Verschmieren" ist aber nicht
als eine Art zeitlicher Mittelwert zu sehen, den wir bemühen weil wir nicht schnell genug hinschauen (so ähnlich
wie ein "verschmierter" Propeller beim Flugzeug), sondern das Elektron ist
diese "Verschmierungswolke", oder, um endlich einen Namen ohne Anführungszeichen zu haben, das Elektron ist das s - Orbital, falls es sich in diesem Zustand befindet.
|
|
 |
Auch den Lateinern sei gesagt: Obwohl in diesem Wort noch die "Umkreisung" des alten
Bohrschen Planetenmodells steckt, hat die lateinische Wurzel hier ihre Bedeutung verloren. Nichts
kreist mehr. |
|
 |
Das Elektron ist mit gleicher Wahrscheinlichkeit (zu jeder
Zeit) an jedem Punkt zu finden, der den Abstand r vom Ursprung hat. Dicht am Ursprung, oder weit weg, ist
die Wahrscheinlichkeit beliebig klein, sie ist am größten (aber keinesfalls = 1) bei einem bestimmten
Radius r0, wie es aus obiger Figur hervorgeht. |
 |
Was bedeutet: "Wahrscheinlichkeit, das Elektron
zu finden"? |
|
 |
Es bedeutet, daß nur das Eingreifen von außen,
eine Messung mit einem geeigneten Gerät, durchgeführt von einem "Beobachter",
eine eindeutige Aussage darüber machen kann, wo die durchgeführte Messung das Elektron gefunden hat.
|
|
 |
Für diese Messung (und nur für diese) ist der
Ort, an dem das Elektron war, dann präzise bekannt. Wiederholt man die Messung
mit exakt denselbem Ausgangsbedingungen, findet man einen anderen Ort. |
|
 |
Das ist zwar in der Wirkung so ähnlich wie beim Würfeln,
aber es ist vom Prinzip her total anders! Würde man ein Würfelexperiment mit exakt denselbem
Ausgangsbedingungen wiederholen, würde man exakt dieselbe Zahl würfeln! Die "Statistik" beim
Würfeln kommt vom "Nicht wissen", sie ist nicht ein integraler Teil des
Systems. |
 |
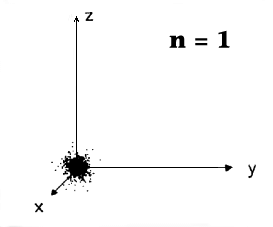
Wiederholt man die Messung oft und zeichnet die gefundenen Positionen (zur Vereinfachung
nur zweidimensional) in ein Koordinatensystem ein, erhält man für ein "s"-Elektron folgende Bilder: |
| |
 |
 |
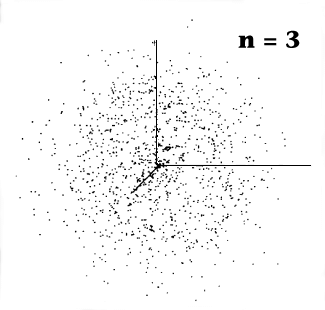 |
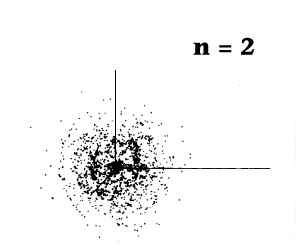
"Experimentelle"
Darstellung der s - Orbitale.
Hier wurde ein Experiment durchgeführt (per Simulation im Computer): Mit
einer geeigneten Anordung wird der exakte Ort eines Elektrons "gemessen". Der gefundene Ort wird als Punkt in
ein x,y,z - Koordinatenkreuz eingetragen. Danach wird das Experiment wiederholt, der jetzt gefundene Punkt
eingetragen, usw. Die entstehende Punktwolke gibt dann einen unmittelbaren visuellen Eindruck über die Wahrscheinlichkeit,
das Elektron bei der Koordinate x,y,z zu finden. |
|
 |
Alle
s-Orbitale sehen ähnlich aus, sie haben jedoch verschiedene räumliche Ausdehnungen
und verschiedene Energien E. Für n = 1 ist das Elektron mit größter Wahrscheinlichkeit
näher am Atomkern zu finden als für größere n; es hat überdies die kleinste
Energie (d.h. die betragsmäßig größte negative Zahl), d.h. ist
am stärksten an den Kern gebunden. Für größere Hauptquantenzahlen
ist es "weiter weg" und schwächer gebunden. |
 |
Das Bild gibt exakt die Wahrscheinlichkeiten wieder, die man
mit der Schrödingergleichung ausgerechnet hat. Und mehr als Wahrscheinlichkeiten kann man
nicht ausrechnen. In der Quantentheorie gibt es nur noch Gewißheit
bezüglich der (direkt nicht meßbaren) Wellenfunktion, aber nicht mehr bei den beobachtbaren (d.h. direkt meßbaren)
Größen! |
|
 |
Diese Tatsache hat bis heute zu ungelösten philosophischen Fragen über das Wesen
der Quantentheorie geführt. Die tiefste Frage ist vielleicht aber, um mit Steven Weinberg
zu sprechen, ob all diese "tiefen" philosophischen Fragen in Wahrheit vielleicht völlig bedeutungslos sind,
und uns nur durch unsere Sprache, die in einer "klassischen"
Welt evolutionär entstand, suggeriert werden! |
 |
Da aber noch nie, seit mit der Quantenmechanik gerechnet
wird, irgendetwas falsch herausgekommen ist, d.h. irgendetwas in einem Experiment anders gemessen wurde als vor- oder nachher
berechnet, brauchen wir uns um die "Bedeutung" der Quantenmechanik nicht weiter
zu kümmern, falls wir "nur" verstehen wollen, was die Welt im Innersten zusammenhält, wie ein Transistor
funktioniert,oder warum Glas bricht, wenn man mit dem Hammer draufhaut, Gummi aber nicht. |
|
 |
Trotzdem gehört es zur Allgemeinbildung - wenigstens in der naturwissenschaftlich-technischen
Welt - ein Minimum an Einblick in die metaphysischen, d.h. philosophischen Fragen nach der Bedeutung der Quantenmechanik
zu besitzen. Ein Schlagwort wie "Schrödingers
Katze" sollte zumindest so weit bekannt sein, daß man es den ungelösten (philosophischen) Paradoxa der
Quantentheorie zuordnen kann. Die aufgeführten Bücher zur Quantentheorie
geben dazu reichlich Material. |
|
 |
Aber nochmals soll betont werden: Wie auch immer diese
Fragen beantwortet (oder neuformuliert) werden; sie sind für die Ausübung der Materialwissenschaft nicht
wichtig. Solarzellen, Chips, Farbfernseher, Flugzeugturbinen, Laser, Lambdasonden usw. - alles Produkte der Quantentheorie
- funktionieren unabhängig davon, wie man zur "Philosophie" der Quantentheorie steht. |
 |
Ein Bild sagt mehr als 1.000 Worte. Eine sichtbare Lösung einer komplizierten
Gleichung überzeugt uns doch mehr als die mathematische Formel. |
|
 |
Kann man Wellenfunktionen sehen? Nein - wie soll den was komplexes aussehen? Aber y(x,y,z) · y*(x,y,z) kann man seit wenigen Jahren
sehen - wie, steht im Link. |
| | |
 |
Als nächstes sind die d-Orbitale zu betrachten.
Wir brauchen mindestens die Hauptquantenzahl n = 3, damit die Nebenquantenzahl den Wert l = 2 annehmen kann.
|
 |
In der jetzt (hoffentlich) vertrauten y Darstellung
ergibt sich folgendes Bild: |
| |
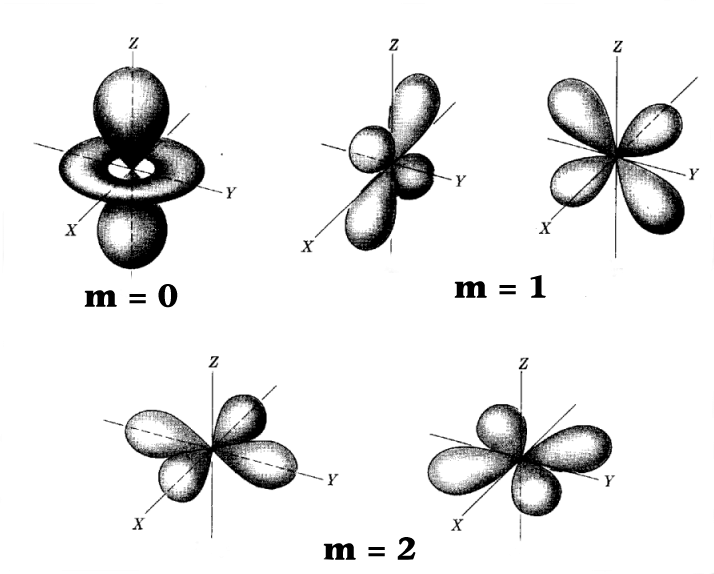 |
Darstellung der Maxima von y für
die l = 2 oder d
- Orbitale.
Beim Übergang zu Aufenthaltswahrscheinlichkeiten
gibt es wieder Verzerrungen, doch bleibt die Symmetrie erhalten. |
|
 |
Das sieht alles ganz kompliziert aus. Ist es auch - aber, wie schon bemerkt, es
ist nicht komplizierter als eine Darstellung der Schwingungsbäuche oder -knoten derLuft in einer Okinara, einem Cello
oder sonst einem Musiklinstrument. |
|
 |
Es ist sogar einfacher, da wir hier perfekte Kugelsymmetrie haben, was in einem Musikinstrumente nicht
gegeben ist. |
|
 |
Im Zweidimensionalen kennen wir das alles. Betrachten wir die Schwingungsmoden einer eingespannten Membran
(z.B einer Trommel), erhalten wir experimentell die altbekannten Chladnischen Klangfiguren;
im Link zu sehen. |
|
 |
Auch wenn wir das nicht so ganz leicht ausrechnen können: Das Experiment zeigt sehr einfach, dass
1. (viele) Lösungen existieren, 2. darunter komplexe Figuren sind, die mathematisch nicht ganz einfach
dargestellt werden können, und 3. Die Trommelmembran (im Gegensatz zu uns) aber keine Probleme hat, die entsprechende
Differentialgleichung zu lösen. |
 |
Eine Frage drängt sich jetzt vielleicht auf: Kann man all diese schönen
berechneten Orbitale und Wellenfunktionen auch irgendwie direkt sehen? Mit einem Elektronenmikroskop
oder sowas ähnliches? |
|
 |
Auf diese Frage gibt es keine einfache Antwort, aber ganz vorsichtig und mit Einschränkungen
kann man ein leises "Ja" sagen. Mehr dazu in einem eigenen Modul. |
| |
|
 |
Es wird langsam kompliziert. Deshalb hören wir hier auf, denn für unsere
Zwecke müssen wir die möglichen Orbitale nicht im Detail verstehen; wer will kann sich das im Link genauer anschauen. Wir fragen uns lieber, was die magnetische
Quantenzahl
m und die Spinquantenzahl
s noch bewirken. |
 |
Einfach ist die Spinquantenzahl s. Sie bewirkt - soweit es uns an
dieser Stelle interessiert - noch gar nichts. Jede Lösung der Schrödingergleichung für das Wasserstoffatom
ist eine Lösung für ein Elektron mit Spin +1/2
und eine Lösung für ein Elektron mit Spin –1/2. Die Energie ist
(ohne Magnetfelder) immer entartet, d.h. für jeden der beiden möglichen Spins gleich groß.
|
|
 |
Aber bitte jetzt nicht denken, der Spin ist unwichtig! Er ist - unter anderem-
verantwortlich für so wichtige Materialeigenschaften wie Magnetismus! |
|
 |
Außerdem ist die schlichte Tatsache, daß der Spin der Elektronen halbzahlig
ist, letzlich dafür verantwortlich, daß es überhaupt Atome gibt - wir
werden das gleich sehen. |
 |
Ähnliches gilt für die magnetische Quantenzahl m. Sie
ändert zwar, wie man oben sieht, die Form der Orbitale; die Energie ist jedoch beim Wasserstoffatom
bezüglich m ebenfalls entartet, d.h. alle möglichen Zustände
mit verschiedenen l und m haben dieselbe Energie. |
 |
Wir haben ein wichtiges Wort nebenbei eingeführt: Den Zustand
des Elektrons. Der Zustand beschreibt die eine spezifische
Lösung von den vielen möglichen, die beim betrachteten Elektron greift. Der
Zustand eines Elektrons im Wasserstoffatom ist durch die 4 Quantenzahlen hinreichend beschrieben. |
 |
Fassen wir zusammen, was wir für das Wasserstoffatom
gelernt haben: |
| |
Es gibt schon für ein Elektron (und ein Proton) viele
Lösungen der Schrödingergleichung.
Die Lösungen werden durch einen Satz von 4 Quantenzahlen (n, l,
m, s) charakterisiert, zu jedem Satz gehört eine bestimmte
Gesamtenergie und eine bestimmte Orbitalform.
Die Orbitalform ist durch n, l und m
gegeben; sie gibt an, wie hoch die Wahrscheinlichkeit ist, das Elektron in einem gegebenen Raumsegment zu finden.
Beim Wasserstoffatom sind die Energien bezüglich l, m,
s
entartet; d.h. werden nur durch n bestimmt. Sie sind identisch
mit den Energiewerten aus dem Bohrschen Modell. |
|
 |
Welchen Zustand hat oder "besetzt" nun das Elektron,
oder, präziser gefragt, welche der mögliche Lösungen "sucht es sich aus"? |
|
 |
Ganz auf sich gestellt, wird es immer den Zustand mit der kleinsten
Energie aufsuchen, den sogenannten Grundzustand, also den 1s1
- Zustand mit n = 1, l = 0 (or "s"), m
= 0, s = +½ oder –½ |
|
 |
Da die Quantenzahlen m und s hier unwichtig sind, vergessen
wir sie und kürzen den Zustand ab wie folgt:
Ein Elektron im Grundszustand ist ein 1s1 Elektron. Die hochgestellte
1 numeriert die Elektronen; d.h. hier haben wir 1 Elektron im 1s Zustand. |
 |
Steht unser Elektron in Wechselwirkung mit dem Rest der
Welt, z.B. durch elektromagnetische Strahlung (inkl. Licht), wird es hin- und wieder genau die richtige Energie
aus dem Strahlungsfeld aufnehmen können, um zu einem der höheren Zustände gelangen zu können.
|
|
 |
Dort wird es einen Weile "sitzen", um dann "von alleine"
auf einen energetisch niedrigeren Zustand zu springen - unter Aussendung eines Photons mit exakt der Energiedifferenz der beiden Zustände.
|
|
 |
Haben wir genügend viele Wasserstoffatome, die bei genügend Energiezufuhr - z.B.
in einer elektrischen Entladung oder im Strahlungsfeld einer Sonne - das ziemlich häufig tun, sehen wir ein leuchtendes
Gas. |
 |
Schauen wir das leuchtende Gas durch ein Spektrometer an, sehen wir scharfe Spektrallinien bei Frequenzen, die exakt den Energiedifferenzen der möglichen Zustände
entsprechen. |
|
 |
Man findet aber nicht alle Frequenzen, die
eigentlich vorkommen könnten. Denn nicht alle Übergänge zwischen Zuständen
sind erlaubt; es gibt sogenannte Auswahlregeln, die angeben welche
Übergänge vorkommen und welche nicht. |
|
 |
Auf diesen beiden Prinzipien: Übergänge zwischen
verschiedenen Zuständen und Auswahlregeln beruht die komplette Spektroskopie.
Wir wollen sie hier jedoch nicht näher verfolgen, sondern uns als nächstes mit den verbliebenen 91 Atomsorten
beschäftigen |
 |
Vorher machen wir aber noch zwei Übungen, eine mehr zum Nachdenken, und eine
richtige, sehr schwere Rechenübung, die uns ein Grundphänomen der Quantentheorie erschließt: Den Tunneleffekt |
| |
|
| |
|
© H. Föll (MaWi 1 Skript)
