3.8 Orbital angular momentum and spin

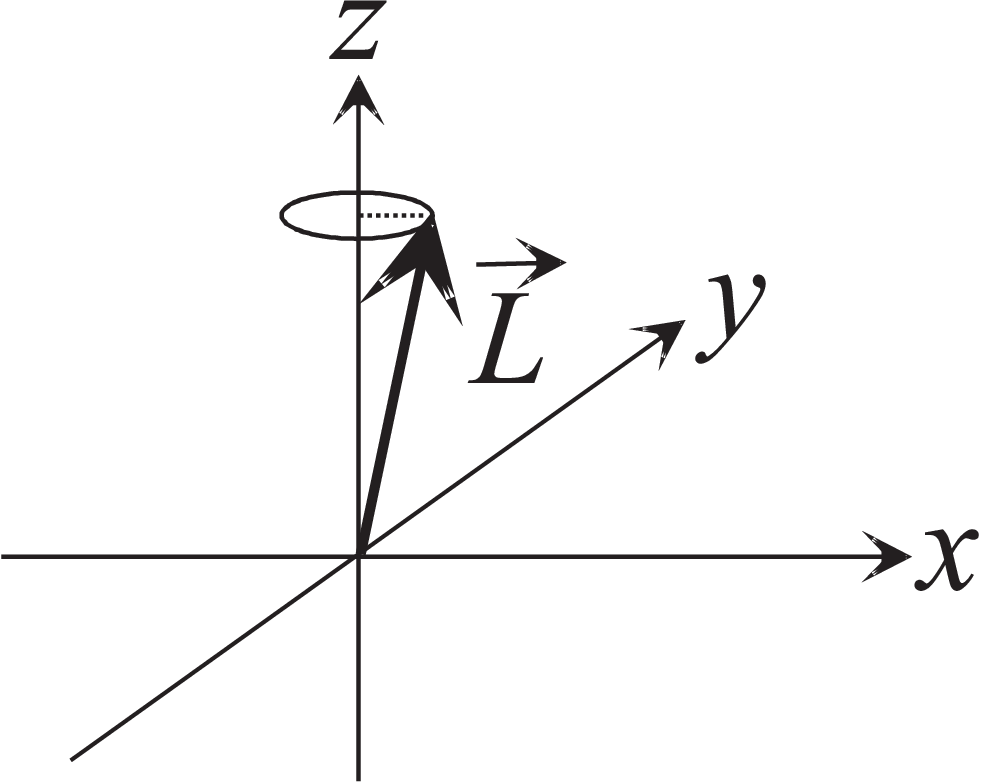
Since the Hamiltonian for atoms shows rotational invariance, the angular momentum is a conserved property. In addition the spin is directly related to angular momentum; it is a form of angular momentum without a classical equivalent. Thus the quantum mechanical description of the angular momentum will be discussed here as one of the first examples, although it is mathematically quite involved.
Classically the angular momentum is defined as

 \begin{equation*} \vec{L}= \vec{r} \times \vec{p} \end{equation*}(3.27)

Following the correspondence principle we therefore get

 \begin{equation*} \hat{ \mathbf{L}}= \hat{ \mathbf{r}} \times \hat{ \mathbf{p}} \end{equation*}(3.28)

for the quantum mechanical operator \(\hat{ \mathbf{L}}\) where \(\hat{ \mathbf{r}}\) and \(\hat{ \mathbf{p}}\) are the operators for position and momentum.
One can easily show (see exercises) that the following relation holds

 \begin{equation*} [\hat{\mathbf{L}}_{x},\hat{\mathbf{L}}_{y}] = - \frac {\hbar}{i} \hat{\mathbf{L}}_{z} \end{equation*}(3.29)

the same commutator relations hold for the cyclic permutation of \(x, y\), and \(z\).
We introduce now a general operator \(\hat{ \mathbf{A}}\) with this commutator relations

 \begin{equation*} \label{l_commutator} \begin{split} [\hat{\mathbf{A}}_{y},\hat{\mathbf{A}}_{z}] & = i \hbar \hat{\mathbf{A}}_{x} \\ {[}\hat{\mathbf{A}}_{z},\hat{\mathbf{A}}_{x}] & = i \hbar \hat{\mathbf{A}}_{y} \\ {[}\hat{\mathbf{A}}_{x},\hat{\mathbf{A}}_{y}] & = i \hbar \hat{\mathbf{A}}_{z} \end{split} \end{equation*}(3.30)
This property of a vectorial observable \(\hat{ \mathbf{A}}\) may be summarized as

 \begin{equation*} \left[\hat{ \mathbf{A}} \times \hat{ \mathbf{A}}\right] = i \hbar \hat{ \mathbf{A}} \end{equation*}(3.31)

The 3 components \(\hat{\mathbf{A}}_{x}, \hat{\mathbf{A}}_{y}\), and \(\hat{\mathbf{A}}_{z}\) are scalar observables (i.e., square matrices with Hermitian symmetry). Let’s introduce another scalar observable:

 \begin{equation*} \hat{ \mathbf{A}}^2 = \hat{\mathbf{A}}_{x} \hat{\mathbf{A}}_{x} + \hat{\mathbf{A}}_{y} \hat{\mathbf{A}}_{y} + \hat{\mathbf{A}}_{z} \hat{\mathbf{A}}_{z} \qquad [\mbox{Note that:}\qquad \hat{ \mathbf{A}}^2 = \hat{ \mathbf{A}}^* \hat{ \mathbf{A}}] \end{equation*}(3.32)

Unlike \(\hat{ \mathbf{A}}\), \(\hat{ \mathbf{A}}^2\) is just a square matrix. It would be classically associated with the square of the length of a classical 3-vector associated with \(\hat{ \mathbf{A}}\) (if there’s one). We will show now, that \(\hat{ \mathbf{A}}^2\) commutates with \(\hat{\mathbf{A}}_{z}\):
Proof: Since the commutator \([\hat{\mathbf{A}}_{z}\hat{\mathbf{A}}_{z}, \hat{\mathbf{A}}_{z}]\) is clearly zero, we have:

 \begin{equation*} [\hat{ \mathbf{A}}^2, \hat{\mathbf{A}}_{z}] = [\hat{\mathbf{A}}_{x} \hat{\mathbf{A}}_{x} + \hat{\mathbf{A}}_{y} \hat{\mathbf{A}}_{y}, \hat{\mathbf{A}}_{z}] = [\hat{\mathbf{A}}_{x} \hat{\mathbf{A}}_{x}, \hat{\mathbf{A}}_{z}] + [\hat{\mathbf{A}}_{y} \hat{\mathbf{A}}_{y}, \hat{\mathbf{A}}_{z}] \qquad . \end{equation*}(3.33)

Each of those two terms can be evaluated using the above commutation relations:

 \begin{equation*} [\hat{\mathbf{A}}_{x} \hat{\mathbf{A}}_{x}, \hat{\mathbf{A}}_{z}] = \hat{\mathbf{A}}_{x} [ \hat{\mathbf{A}}_{x}, \hat{\mathbf{A}}_{z}] + [ \hat{\mathbf{A}}_{x}, \hat{\mathbf{A}}_{z}] \hat{\mathbf{A}}_{x} = - i \hbar (\hat{\mathbf{A}}_{x}\hat{\mathbf{A}}_{y}+\hat{\mathbf{A}}_{y}\hat{\mathbf{A}}_{x}) \end{equation*}(3.34)

 \begin{equation*} [\hat{\mathbf{A}}_{y} \hat{\mathbf{A}}_{y}, \hat{\mathbf{A}}_{z}] = \hat{\mathbf{A}}_{y} [ \hat{\mathbf{A}}_{y}, \hat{\mathbf{A}}_{z}] + [ \hat{\mathbf{A}}_{y}, \hat{\mathbf{A}}_{z}] \hat{\mathbf{A}}_{y} = i \hbar (\hat{\mathbf{A}}_{y}\hat{\mathbf{A}}_{x}+\hat{\mathbf{A}}_{x}\hat{\mathbf{A}}_{y}) \end{equation*}(3.35)

Therefore, those two terms add up to zero and we obtain: \( [\hat{ \mathbf{A}}^2, \hat{\mathbf{A}}_{z} ] = 0\)
The above definition of \( \hat{ \mathbf{A}}^2\) ensures that \(\langle \psi| \hat{ \mathbf{A}}^2 | \psi\rangle \) is non negative for any ket \(|\psi\rangle \) (HINT: this is the sum of 3 real squares).
Therefore, this operator can only have non negative Eigenvalues, which (for the sake of future simplicity) we may as well put in the following form, for some non negative number \(l\).

 \begin{equation*} l (l+1) \hbar^2 \end{equation*}(3.36)

The punch line will be that \(l\) is restricted to integer or half-integer values. For now however, we may just accept this expression because it spans all non negative values once and only once when \(l\) goes from zero to infinity.
So, we may use \(l\) as an index to denote each Eigenvalue of \(\hat{ \mathbf{A}}^2\) . Similarly, we may use another index \(m\) to identify the Eigenvalue \(m \hbar\) of \(\hat{\mathbf{A}}_{z}\). For now, nothing special is assumed about \(m\) (we’ll show later that \(2 m\) is an integer).
Since those two observables commute, there is an orthonormal Hilbertian basis consisting entirely of Eigenvectors common to both of them. We may specify it by introducing a third index \(n\) (needed to distinguish between kets having identical Eigenvalues for each of our two observables). Those conventions are summarized by the following relations, which clarify the notation used for base kets:

 \begin{equation*} \begin{array}{rccl} \hat{ \mathbf{A}}^2 |n,l,m\rangle & = & l (l+1) \hbar^2 & |n,l,m\rangle \\ \hat{\mathbf{A}}_{z} |n,l,m\rangle & = & m \hbar & |n,l,m\rangle \end{array} \end{equation*}(3.37)

To determine the restrictions that \(l\) and \(m\) must obey, we introduce the following two non-Hermitian operators, which are conjugate of each other. They are collectively known as ladder operators; and are respectively called lowering operator (or anihilation operator) and raising operator (or creation operator) because it turns out that each transforms an Eigenvector into another Eigenvector corresponding to a lesser or greater Eigenvalue, respectively.

 \begin{equation*} \hat{\mathbf{A}}_{-} = \hat{\mathbf{A}}_{x} - i \hat{\mathbf{A}}_{y} \qquad \mbox{and} \qquad \hat{\mathbf{A}}_{+} = \hat{\mathbf{A}}_{x} + i \hat{\mathbf{A}}_{y} \end{equation*}(3.38)

Both commute with \(\hat{ \mathbf{A}}^2\) (because \(\hat{\mathbf{A}}_{x}\) and \(\hat{\mathbf{A}}_{y}\) do). The following holds:

 \begin{equation*} ||\hat{\mathbf{A}}_{+} |n,l,m\rangle ||^2 = \langle n,l,m| \hat{\mathbf{A}}_{-} \hat{\mathbf{A}}_{+} |n,l,m\rangle \end{equation*}(3.39)

Where

 \begin{equation*} \begin{split} \hat{\mathbf{A}}_{-} \hat{\mathbf{A}}_{+} & = \hat{\mathbf{A}}_{x} \hat{\mathbf{A}}_{x} + \hat{\mathbf{A}}_{y} \hat{\mathbf{A}}_{y} + i [\hat{\mathbf{A}}_{x}, \hat{\mathbf{A}}_{y}]\\ & = \hat{ \mathbf{A}}^2 - \hat{\mathbf{A}}_{z} \hat{\mathbf{A}}_{z} - \hbar \hat{\mathbf{A}}_{z} \end{split} \end{equation*}(3.40)
So

 \begin{equation*} ||\hat{\mathbf{A}}_{+} |n,l,m\rangle ||^2 = \left[ l (l+1) - m^2 - m \right] \hbar^2 \qquad . \end{equation*}(3.41)

As the non negative square bracket is equal to \(l (l+1) - m (m+1)\) we see that \(m\) cannot exceed \(l\). We would find that \((-m)\) cannot exceed \(l\) by performing the same computation for \(||\hat{\mathbf{A}}_{-} |n,l,m\rangle ||^2\).
Therefore, all told:

 \begin{equation*} -l \leq m \leq l \qquad . \end{equation*}(3.42)

Note that the above also proves that the ket \(\hat{\mathbf{A}}_{+} |n,l,m\rangle \) vanishes only when \(m = l\). Likewise, \(\hat{\mathbf{A}}_{-} |n,l,m\rangle \) is nonzero unless \(m = -l\).
Except in the aforementioned cases where they vanish, such kets are Eigenvectors of \(\hat{\mathbf{A}}_{z}\) associated with the Eigenvalue of index \(m \pm 1\). Let’s prove that:

 \begin{equation*} \hat{\mathbf{A}}_{z}\hat{\mathbf{A}}_{+} - \hat{\mathbf{A}}_{+}\hat{\mathbf{A}}_{z} = [\hat{\mathbf{A}}_{z}, \hat{\mathbf{A}}_{x}] + i [\hat{\mathbf{A}}_{z}, \hat{\mathbf{A}}_{y}] = i \hbar (\hat{\mathbf{A}}_{y} - i \hat{\mathbf{A}}_{x}) = \hbar \hat{\mathbf{A}}_{+} \end{equation*}(3.43)

Therefore,

 \begin{equation*} \hat{\mathbf{A}}_{z}\hat{\mathbf{A}}_{+} = \hat{\mathbf{A}}_{+}\hat{\mathbf{A}}_{z} + \hbar \hat{\mathbf{A}}_{+} \qquad . \end{equation*}(3.44)

So, if \(|\psi \rangle \) is an Eigenvector of \(\hat{\mathbf{A}}_{z}\) associated with the value \(m \hbar\), then:

 \begin{equation*} \hat{\mathbf{A}}_{z}\hat{\mathbf{A}}_{+}|\psi\rangle = (m+1) \hbar \hat{\mathbf{A}}_{+} |\psi\rangle \qquad . \end{equation*}(3.45)

Thus, the ket \(\hat{\mathbf{A}}_{+} |\psi\rangle \) is either zero or an Eigenvector of \(\hat{\mathbf{A}}_{z}\) associated with the value \((m+1) \hbar\). The same is true of \(\hat{\mathbf{A}}_{-} |\psi\rangle \) with \((m-1) \hbar\).
Since we know that \(m\) is between \(-l\) and \(+l\) , we see that both \(l - m\) and \(l + m\) must be integers (or else iterating one of the two constructions above would yield a nonzero Eigenvector with a value of \(m\) outside of the allowed range). Thus, \(2 l\) and \(2 m\) must be integers (they are the sum and the difference of the integers \(l + m\) and \(l - m\)). If \(l\) is an integer, so is \(m\). If \(l\) is an half-integer, so is \(m\) (by definition, an ”half-integer” is half the value of an odd integer).
The above demonstration is quite remarkable: It shows how a 3-component observable is quantized whenever it obeys the same commutation relation as an orbital angular momentum. Although half-integer values of the numbers l and m are allowed, those do not correspond to an orbital momentum but to a quantum mechanical spin. Only orbital momenta can lead to whole numbers of \(l\) and \(m\) (which we will not proof here).


PIC


Fig. 3.1: The uncertainty of an angular momentum in \(x\) and \(y\) is represented by a rotation around the \(z\)-axis.


Fig. 3.1 schematically illustrates the above relations for \(m = l\). The length \(L\) of the angular momentum vector \(\hat{ \mathbf{L}}\) equals \(L = \hbar \sqrt{l (l+1)}\) and is just somewhat larger than \(L_z = \hbar l\). \(\hat{\mathbf{L}}_{z}\) and \(\hat{ \mathbf{L}}\) can be measured simultaneously, i.e. they have the same Eigenvector system. We expect an uncertainty in \(\hat{\mathbf{L}}_{x}\) and \(\hat{\mathbf{L}}_{y}\) since both operators do not commutate with \(\hat{\mathbf{L}}_{z}\). This is represented by the rotation of the angular momentum vector around the \(z\)-axis.
All Hamilton operators which commutate with an operator \(\hat{ \mathbf{A}}\) showing the commutator relations of Eq. (3.30) will have Eigenvector and Eigenvalues as discussed in this section. As we will see later, the commutator between a Hamilton operator and an operator \(\hat{ \mathbf{A}}\) is related to symmetries, represented by such an operator. Having discussed the next section we will be able to state that all systems which show rotational invariance will have an Eigenvector system \(|n,l,m\rangle \), where \(l\) and \(m\) are integer (half integer) numbers and indicate quantum numbers.
Until now we did not need any explicit representation of the Eigenfunctions \(|n,l,m\rangle \). It is the very famous set of spherical harmonic functions which are defined as

 \begin{equation*} Y_{lm}(\Theta, \Phi):= \frac{1}{\sqrt{2\pi}} N_{lm} P_{lm}(\cos\Theta) e^{i m \Phi} \qquad . \end{equation*}(3.46)

Here the adjoined Legendre polynomials are defined as

 \begin{equation*} P_{lm}(x):= \frac{(-1)^m}{2^l l!} \left(1 - x^2 \right)^{\frac{m}{2}} \frac{d^{l+m}}{dx^{l+m}}\left( x^2 - 1 \right)^l \qquad , \end{equation*}(3.47)

and the scaling factor

 \begin{equation*} N_{lm}(x):= \sqrt{\frac{2l+1}{2}\frac{(l-m)!}{(l+m)!}} \end{equation*}(3.48)

The first spherical harmonic functions are

\(Y_{lm}\)\(l=0\)\(l=1\)\(l=2\)\(l=3\)
\(m = -3\) \(+\sqrt{\frac{35}{64 \pi}}\sin^3 \Theta e^{-3i\Phi}\)
\(m = -2\) \(+\sqrt{\frac{15}{32 \pi}}\sin^2 \Theta e^{-2i\Phi}\)\(+\sqrt{\frac{105}{32 \pi}} \sin^2\Theta \cos \Theta e^{-2i\Phi}\)
\(m = -1\) \(+\sqrt{\frac{3}{8 \pi}}\sin \Theta e^{-i\Phi} \)\(+\sqrt{\frac{15}{8 \pi}}\sin \Theta \cos \Theta e^{-i\Phi}\)\(+\sqrt{\frac{21}{64 \pi}} \sin \Theta \left(5 \cos 2 \Theta - 1 \right)e^{-i\Phi}\)
\(m = 0\) \(+\sqrt{\frac{1}{4 \pi}}\)\(+\sqrt{\frac{3}{4 \pi}}\cos \Theta\)\(+\sqrt{\frac{5}{16 \pi}}\left( 3 \cos^2 \Theta -1 \right)\)\(+\sqrt{\frac{7}{16 \pi}} \left( 5 \cos^3 \Theta - 3\cos \Theta \right)\)
\(m = 1\) \(- \sqrt{\frac{3}{8 \pi}}\sin \Theta e^{i\Phi} \)\(-\sqrt{\frac{15}{8 \pi}}\sin \Theta \cos \Theta e^{i\Phi}\)\(-\sqrt{\frac{21}{64 \pi}} \sin \Theta \left(5 \cos 2 \Theta - 1 \right)e^{i\Phi}\)
\(m = 2\) \(+\sqrt{\frac{15}{32 \pi}}\sin^2 \Theta e^{2i\Phi}\)\(+\sqrt{\frac{105}{32 \pi}} \sin^2\Theta \cos \Theta e^{2i\Phi}\)
\(m = 3\) \(-\sqrt{\frac{35}{64 \pi}}\sin^3 \Theta e^{3i\Phi}\)

With frame Back Forward as PDF

© J. Carstensen (Quantum Mech.)