|
Nach dem einfachsten Atom, demWasserstoff, ist das nächst einfache Atom das
Helium mit der Ordnungszahl 2. Es hat im neutralen Zustand 2 Elektronen. |
|
 |
Um die Schrödingergleichung für das System aufstellen zu können,
brauchen wir die potentielle Energie der Elektronen. Die Beziehung dafür kann noch einfach formuliert werden. Dazu
addieren wir die potentiellen Energien von Elektron 1 und Elektron 2 im Feld des Atomkerns sowie die potentielle
Energie, die aus der Abstoßung der beiden Elektronen resultiert. |
| |
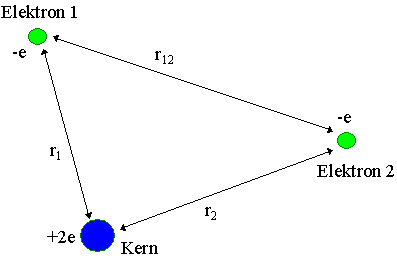 |
U(r1, r2, r12) = - ze2/r1 -
ze2/r2 + e2/r12
|
|
 |
Die Abstandsvektoren r1, r2,
r12 sind eindeutig durch die (mathematischen) Koordinaten x1, y1,
z1 und x2, y2, z2 der beiden
Elektronen gegeben, damit ist auch U eine Funktion dieser Koordinaten. |
 |
Damit läßt sich die Schrödingergleichung hinschreiben; es ist
einfach das obige Potential einzusetzen. Die Wellenfunktion y hängt jetzt aber von
den Koordinaten x1, y1, z1
und
x2, y2, z2 ab, d.h. von einem Ort r1
und einem Ort r2. |
|
 |
Damit wird die Wellenfunktion eine Funktion mit 6 Variablen: |
| |
| y | = |
y(x1, y1, z1, x2, y2,
z2) |
|
|
 |
Was bedeutet das? |
|
 |
Wie zuvor, gibt das Betragsquadrat von y = y
· y*, die Wahrscheinlichkeit an, die Elektronen
irgendwo zu finden. Für die Orte r1 und r2 ist y
· y* damit die Wahrscheinlichkeits(dichte), das erste Elektron am Ort
r1 = (x1, y1, z1)
und gleichzeitig das zweite Elektron am Ort r2 = (x2,
y2, z2) zu finden. |
|
 |
Beim Würfeln mit zwei Würfeln wäre das nichts anderes, als die Wahrscheinlichkeit
w(2, 5), z.B. mit einem Würfel eine 5 und mit dem anderen eine 2 zu würfeln.
Das ist übrigens etwas anderes, als die Wahrscheinlichkeit w(7), d.h. mit zwei Würfeln eine 7
zu würfeln. Es lohnt sich, darüber mal kurz nachzudenken - wir werden das noch brauchen! |
|
 |
y(r1, r2), und gleichzeitig
die Gesamtenergie E, ergeben sich wiederum aus der Lösung der Schrödingergleichung für diesen
Fall. Die Kenntnis von y enthält wiederum alle
Informationen über das System - unser He-Atom - die es gibt; aus y lassen
sich alle meßbaren Größen berechnen. |
 |
So weit, so gut. Leider können weder wir, noch sonst jemand, die Schrödingergleichung
für zwei (oder mehr) Elektronen geschlossen lösen (das ist so ähnlich wie in der Himmelsmechanik das Dreikörperproblem;
z.B. Sonne, Erde und Mond). Selbstverständlich gibt es Näherungen; spätestens bei "komplizierten"
Atomen oder Molekülen mit vielen Elektronen, sind aber auch Näherungen für Lösungen des Gesamtsystems
nicht mehr ganz einfach machbar. |
|
 |
Damit sind wir erst mal in einer Sackgasse, glücklicherweise gibt es aber einen Ausweg:
Man kann eine extrem simple Näherung machen, die eine einfache und qualitativ richtige
Betrachtung auch komplizierter Atome erlaubt, allerdings keine guten Zahlenwerte mehr liefert. |
|
 |
Der Trick ist, nicht alle Elektronen
eines Atoms zu betrachten, sonden nur eines. Gedanklich denken wir uns die restlichen
Elektronen gleichmäßig über das Volumen des Atoms verschmiert. Das eine übriggebliebene Elektron "sieht"
dann nur eine irgendwie verschmierte positive Ladung, da die negativen Ladungen der
verschmierten Elektronen die Kernladung bis auf eine Elementarladung kompensieren. |
|
 |
Damit haben wir die Betrachtung unseres beliebigen Atoms vereinfacht auf die Betrachtung eines
Atoms, das dem Wasserstoffatom sehr ähnlich ist: Ein Elektron ist im Potential einer
positiven Elementarladung zu betrachten - allerdings ist diese positive Ladung nicht mehr punktförmig. |
 |
Wir erhalten dann als Lösung der Schrödingergleichung Wellenfunktionen
für das eine Elektron, die völlig analog zu den Lösungen des Wasserstoffatoms sind.
|
|
 |
Da aber das Potential kein Punktpotential mehr ist, und das ganze ja nur eine Näherung darstellt, können wir weder erwarten, daß die Zahlenwerte für
die Gesamtenergie noch stimmen, noch gibt es einen Grund anzunehmen, daß die Energie weiterhin bezüglich der
Quantenzahlen l, m, und s entartet ist. Auch die genaue Form der Orbitale könnte etwas anders sein.
|
|
 |
Aber s-Orbitale bleiben kugelsymmetrische s-Orbitale, die Keulen der p-Orbitale
bleiben Keulen, usw. usf.. Mit diesem Ansatz erhalten wir - ohne überhaupt zu rechnen
- folgendes Ergebnis: |
|
 |
Jede Lösung der Schrödingergleichung für
ein Elektron in einem beliebigen Atom wird weiterhin durch die vier Quantenzahlen n, l, m, s beschrieben. |
|
 |
Als Wellenfuktion für das eine Elektron, das wir
herausgegriffen haben, stehen - leicht modifiziert - die Wellenfunktionen des Wasserstoffatoms zur Verfügung. Insbesondere
sind die Orbitalformen in ihren Symmetrien unverändert. |
|
 |
Zu jedem Satz von Quantenzahlen gehört weiterhin eine Gesamtenergie E;
allerdings kann der Zahlenwert sehr verschieden von den Wasserstoff-Werten sein. |
|
 |
Die beim Wasserstoffatom vorliegende Entartung (E nur abhängig von n,
nicht von l, m und s) muß nicht mehr vorliegen; zur selben Hauptquantenzahl
n können - je nach l, m und s - verschiedene
Gesamtenergien vorliegen. |
 |
Damit kann ein Atom als ein System verstanden werden, das für die gebundenen
Elektronen bestimmte Orbitale als mögliche Elektronenzustände aufweist, charakterisiert durch einen Satz von Quantenzahlen
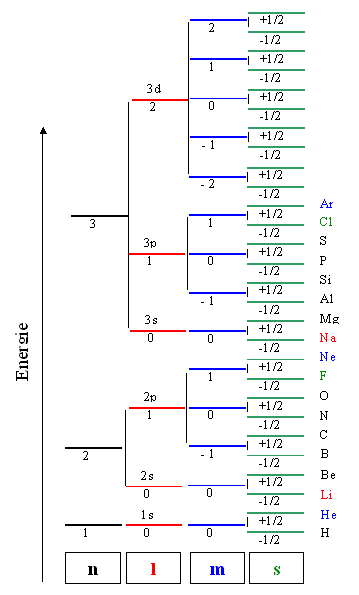
und eine zugehörige Gesamtenergie. Graphisch stellt man dies häufig ganz schematisch in einem Quantenzahlen
- Energie Diagramm dar: |
|
|
|
|
 |
Allerdings nehmen wir am Rande war, dass dies eine rein schematische Auftragung
ist. Die wahre Energie, die zu einem Satz von Quantenzahlen gehört, folgt nicht dem einfachen "Leiter" Schema
der Graphik, das immer gleiche Abstände zwischen den Energie "Sprossen" zeigt. Insbesondere kehrt sich gelegentlich
sogar die Reihenfolge um, z.B. liegen die 3d - Energieniveaus högher als das 4s Niveau - deswegen stehen
nach Ar auch keine Elementsymbole mehr an den Niveaus. Mehr dazu in einem eigenen
Modul. |
|
Besetzung der verfügbaren Zustände mit Elektronen |
| | |
 |
Nehmen wir als Beispiel jetzt ein Silizium
Atom, dann müssen wir 14 Elektronen auf die vorhandenen Zustände verteilen. Geben wir auf jeden Zustand
ein Elektron, landen wir beim 3p2 (d.h. wir haben zwei Elektronen
auf den zu n = 3 und l = p gehörenden 6 Zuständen); für die anderen Elemente gilt entsprechendes.
|
|
 |
Die Energien sind hier völlig willkürlich dargestellt; sie sind bei jedem Atom anders. Allerdings
bleibt die ungefähre Wichtung erhalten: Zustände mit kleinen Quantenzahlen;
damit großen Aufenthaltswahrscheinlichkeiten in Nähe des Atomkerns, liegen energetisch "tief".
Die Elektronen sind stark gebunden; man bräuchte viel Energie um sie aus dem Atom abzulösen. |
 |
Im obigen Bild sind die Elektronen gleichmäßig auf die verfügbaren
Zustände verteilt, aber nach welchem Kriterium? Wie
beim Wasserstoffatom fragen wir uns wieder, wo die Elektronen nun sind, welche Zustände sie jetzt wirklich besetzen. |
|
 |
Die intuitive Antwort, basierend auf der klassischen Physik, wäre,
daß sie alle - oder doch fast alle - auf dem energetisch tiefsten Niveau sich befinden, da wir zu wissen glauben,
daß alle sich selbst überlassenen Systeme zum Minimum der Energie
streben. Aber |
|
|
Die Intuition ist völlig falsch!
(die klassische Physik hier auch) |
|
 |
Denn in der Welt der Quantenphysik gilt das nach dem Physiker Wolfgang Pauli benannte Pauli
Prinzip, auch Paulisches Auschließungsprinzip genannt. Es ist von ungeheurer
Wichtigkeit und besagt etwas sehr einfaches: |
|
|
Teilchen mit halbzahligem Spin
(und dazu gehören die Elektronen)
dürfen nie Zustände einnehmen,
die in allen Quantenzahlen übereinstimmen. |
|
 |
Was ist der Spin eines Teilchens?
Am besten ist es, sich den Spin als ist eine elementare Eigenschaft vorzustellen, die
ein Teilchen hat, und die nicht ohne Zerstörung des Teilchens geändert werden kann. |
|
 |
Es ist so ähnlich wie bei der (Elementar)ladung oder der Masse eines Elektrons (oder
anderen Elementarteilchens): Es sind Eigenschaften des Teilchens, die es hat und die wir messen können. Was
aber eine Ladung "eigentlich" ist - das "weiß" niemand. |
|
 |
Ähnlich wie die Ladung oder die Masse, gibt es auch den Spin
auch nur in festen, unabänderlichen und unzerstörbaren (in diesem Fall dimensionslosen) Werten |
|
 |
Entdeckt wurde der Spin 1926, mehr dazu im Link. |
 |
Der Spin ist nicht direkt meßbar, er
erscheint je nach experimenteller "Blickrichtung" entweder als Drehimpuls
oder als magnetisches Moment. |
|
 |
Im Gegensatz zur elektrischen Ladung ist der Spin s
aber so etwas ähnliches wie ein Vektor; man denke sich dazu einen kleinen Pfeil
der Länge 1/2 und Richtung "up" oder "down", "links" oder "rechts" - wie es beliebt.
|
|
 |
Mit einem Spin verkoppelt ist immer ein mechanischer Drehimpuls S. Dieser Spindrehimpuls ist sehr einfach zu berechnen; wir haben (etwas salopp formuliert) |
| |
| S | = |
s · 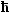 |
|
|
|
 |
Für ein Elektron (oder Proton, oder Neutron , oder ....) findet man S relativ
zu einer willkürlichen Achse immer nur mit den Werten + 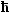 /2 oder – /2 oder –
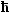 /2; d.h. unser kleiner Pfeil zeigt in die gewählte Richtung (+) oder in die Gegenrichtung (–);
aber nie woanders hin. . /2; d.h. unser kleiner Pfeil zeigt in die gewählte Richtung (+) oder in die Gegenrichtung (–);
aber nie woanders hin. . |
 |
Das Plancksche Wirkungsquantum hat hier die Funktion des elementaren
Drehimpulsquants. Man ist damit versucht, sich das Teilchen als kleinen Kreisel vorstellen; aber das ist eine
Analogie die nicht weit trägt. |
|
 |
Denn das kleine Magnetchen, oder genauer gesagt, das magnetische Moment, das sich beispielweise
bilden müßte, wenn eine Ladung im Kreis herumläuft - wie es bei einem geladenen Kügelchen, als das
man sich ein Elektron mit Drehimpuls ja vorstellen müßte - liegt zwar in Form des magnetischen Moments des Elektrons
vor, aber es hat den "falschen" Zahlenwert |
|
 |
Magnetisches Moment heißt, daß das Elektron (oder ein anderes Elementarteilchen)
sich wie ein kleiner Stabmagnet mit Nord- und Südpol benimmt. Jede Ladung die sich im Kreis bewegt hat ein magnetisches
Moment, aber interessanterweise hat auch das elektrisch neutrale Neutron ein magnetisches Moment. Wir nehmen einfach mal
hin, daß auch das magnetische Moment eines Elementarteilchens
gequantelt ist und einen bestimmten Teil einer elementaren Einheit besitzt, dem Bohrschen
Magneton
mB = 1.1654 · 10– 29 Vsm. Mehr im Link. |
 |
Alle Elementarteilchen besitzen einen halb- oder ganzzahligen Spin (wenn man,
etwas sophistisch, Spin = 0 als ganzzahlig mitrechnet). Der Spin eines Teilchens ist wie die elektrische Ladung immer
gequantelt, d.h. kommt immer nur als Vielfaches von + ½ oder – ½ vor. |
|
 |
Elementarteilchen haben damit immer eine halbzahlige
oder ganzzahlige Spinquantenzahl, oder salopp ausgedrückt, Spin, z.B. s
= 1/2, s = 3/2, oder s = 0, s = – 1, s = 2. Teilchen mit halbzahligem
Spin - die Fermionen - sind insbesondere: |
|
 |
Elektronen: Ihr Spin ist ± ½. |
|
 |
Protonen und Neutronen: Ihr Spin
ist ebenfalls ± ½. |
|
 |
Exoten, wie das Omega
-Teilchen mit Spin ±3/2. |
|
 |
Alle diese Teilchen haben den Spin 1/2 oder ein Vielfaches von ½; man nennt
alle Teilchen mit halbzahligem Spin
Fermionen (nach dem Physiker Enrico Fermi)
- in der Einführung in die Materialwissenschaft Teil II werden wir lernen, warum. |
 |
Teilchen mit ganzzahligem Spin - man nennt
sie nach Chandraseka Bose generell Bosonen
- sind: |
|
 |
Mesonen (die Teilchen die die Bindungskräfte im Atomkern
vermitteln). Ihr Spin ist 0 |
|
 |
Photonen, die "Lichtteilchen". Sie sind in diesem Zusammenhang
ganz wichtig; ihr Spin ist 1. |
 |
Spätestens beim Beispiel des Photons wird klar, daß die Vorstellung
des Spins als ein sich drehendes "Kügelchen" seine Tücken hat. Es ist besser, den Spin eines Teilchens
als elementare Eigenschaft zu akzeptieren, die ähnlich wie die Ladung immer erhalten bleibt. |
 |
Das Pauli-Prinzip hat weitreichende Konsequenzen; wir werden einige davon noch
kennenlernen. |
|
 |
Aber warum gilt es? Was ist so fundamental verschieden
zwischen Fermionen und Bosonen? |
|
 |
Hier liegt eine der tiefsten Fragen der Physik versteckt. Selbst Richard Feynman, berühmt dafür, daß er selbst die kompliziertesten Dinge
einfach (und trotzdem richtig) erklären konnte, hat hier das Handtuch
geworfen - man muß das Pauli-Prinzip einfach als Naturgesetz akzeptieren. |
| | |
 |
Die Besetzung der bei einem Atom vorhandenen Zustände unter Berücksichtigung
des Pauli-Prinzip ist nun einfach: Wir starten mit der kleinsten Quantenzahl und füllen das dadurch definierte Energieniveau
mit einem Elektron. Wir bekommen das Wasserstoffatom im Grundzustand. Die Quantenzahlen
des Elektrons sind |
|
 |
n = 1, l = 0, m = 0, s = +1/2. Da im Kontext des
hier behandelten Atommodells der Spin sich als Drehimpuls "zeigt", müssen wir das Vorzeichen betrachten.
Wir hätten auch s = – ½ nehmen können; aber wir müssen uns für eine der beiden Möglichkeiten
entscheiden; welche ist egal. Zur leichteren Ansprache nennen wir es ein 1s1 - Elektron. |
|
 |
Das He - Atom braucht ein weiteres Elektron; dieses hat nun dem Pauli-Prinzip folgend
die Quantenzahlen n = 1, l = 0, m = 0, s = - ½. In der Kurzschreibweise ist es ein 1s2
- Elektron. Die 2 als "Hochzahl" am s drückt dabei nur aus, daß es das zweite
Elektron ist, das diesen Zustand besetzen kann - ob man ihm Spin ½ oder - ½ zuschreibt, ist willkürlich.
Alle zu n = 1 gehörenden Orbitale sind jetzt besetzt, wir haben eine vollständig
gefüllte erste "Schale". |
|
 |
Für das Li - Atom mit drei
Elektronen hat es auf den 1s-Niveaus, die durch n = 1 und l = 0 definiert sind, keinen
Platz mehr. Das nächste Niveau ist durch s = 2, l = 0, m = 0, s = +1/2 definiert, wir bekommen
das 2s1 - Elektron. Wir haben jetzt begonnen, die n = 2 Schale zu besetzen; sie kann insgesamt
8 Elektronen aufnehmen. |
|
 |
Davon 2 für den s - Zustand, und 6 im p - Zustand. Die Hochzahl
gibt dabei immer an wieviele der vorhanden Zustände s,p,d,... besetzt sind; sie kombiniert dabei die Quantenzahlen
m und s. |
|
 |
Und so weiter und so fort. Dieses Bildungsprinzip ist
im obigen Bild schon berücksichtigt. |
 |
In der schematischen Grafik ist jeder Zustand bei einer anderen Energie eingezeichnet,
das kann, aber muß nicht sein, da einige Zustände ja entartet sein können, d.h. dieselbe Energie besitzen. |
 |
Uns fällt auf: Immer wenn in einer Schale die p - Niveaus vollständig
gefüllt sind, d.h. alle möglichen Zustände durch Elektronen besetzt sind, ist das zugehörige Atom ein
Edelgas - wir reden von einer vollbesetzten Schale. |
|
 |
Edelgase sind edel, weil
sie so gut wie nicht mit anderen Elementen reagieren und keine Moleküle bilden - nicht mal mit sich selbst. Deshalb
sind sie Gase, denn eine Flüssigkeit oder ein Festkörper verlangt per definitionem,
daß ein Atom sich an andere Atome "bindet". |
|
 |
Wir wissen, daß die Neigung Bindungen einzugehen von der Temperatur
abhängt; bei hohen Temperaturen ist alles gasförmig. Aber Edelgase bleiben auch bei extrem tiefen
Temperaturen noch gasförmig; Helium verflüssigt erst 4 K über dem absoluten Nullpunkt (und wird
überhaupt nie fest)! Sie sind also chemisch inert. |
 |
Auch die Elemente, denen gerade noch ein Elektron für eine vollbesetzte Schale
fehlt, sind sich chemisch ähnlich; dasselbe gilt für die Elemente, die eines
zuviel besitzen. |
|
 |
Wir haben die chemischen Familien der Halogenide beziehungsweise
Alkalimetalle - beides äußerst reaktive und aggressive Elemente, die in der
Natur deshalb auch nie elementar vorkommen, sondern immer nur im Verbund mit anderen Atomen. |
 |
Offenbar gibt es Regeln, die allgemeine chemische Eigenschaften und gefüllte
Elektronenzustände miteinander verknüpfen. Sie sollen im nächsten Unterkapitel angesprochen werden. |
| |
|
© H. Föll (MaWi 1 Skript)