Pauli-Prinzip

	Es gibt, wie schon an anderer Stelle ausgeführt, keine einfache und sofort einleuchtende Erklärung zum Pauli Prinzip. Man kann es jedoch mit anderen Eigenschaften von Elementarteilchen korrelieren und dann etwas tiefgründiger formulieren.
		Entscheidend ist zunächst die Tatsache, daß Elementarteilchen prinzipiell ununterscheidbar sind. Das leuchtet zwar irgendwie ein, aber im Grunde ist es ein Axiom.
	Das hat viele Konsequenzen, eine davon ist sofort einsichtig.
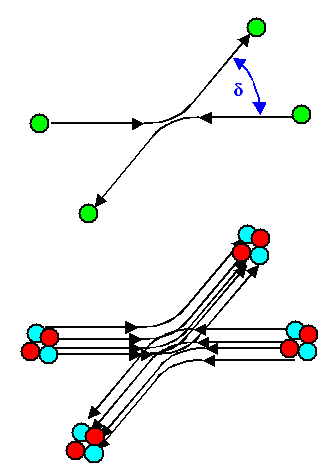
		Wir lassen mal gedanklich zwei Elementarteilchen derselben Sorte - zwei Elektronen - oder zwei identische Kombinationen z.B. - zwei a - Teilchen (= zwei He Kerne) wie Billardkugeln aufeinanderstoßen. Ein mögliches Ergebnis ist im Bild links unten dargestellt
		Die Bestandteile des a Teilchens sind zwei rote Protonen und zwei blaue Neutronen
		Der Stoß ist bei gleichen Impulsen und Energien symmetrisch, mit entsprechenden Detektoren finden wir die Teilchen an den Positionen wie eingezeichnet.
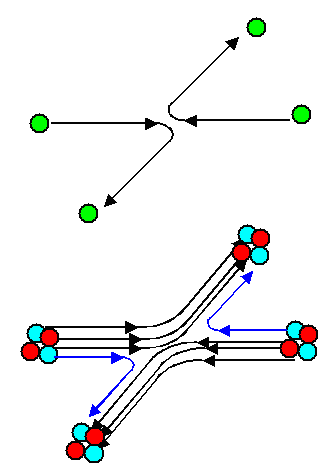
	Da aber die einzelnen Teilchen prinzipiell ununterscheidbar sind, hätte der Stoß bei identischen Ausgangsbedingungenen auch wie rechts eingezeichnet stattfinden können (bei den a Teilchen wurde z.B ein Neutron ausgetauscht)
		Es gibt offenbar für einen gegeben Streuwinkel d mehrere prinzipiell ununterscheidbare Wege zu ein und demselben Endergebnis am Ort des (nicht eingezeichneten) Detektors.
		Das bedeutet in der formalen Sprache der Wellenfunktion, daß die Wahrscheinlichkeitsamplitude für Streuung unter einem bestimmten Winkel d, also y(d)n · y(d)*n für jeden spezifischen Weg n der zum selben Ergebnis am Ort des Detektors führt, identisch sein muß.
		Für die Wellenfunktionen selbst bedeutet das, daß sie bis auf einen Phasenfaktor exp if, der bei der Betragsquadratbildung herausfällt, identisch sein müssen, d.h.
		y(d)n  =  y(d)m · exp ifn, m
	Betrachtet man nun konkrete Fälle, erhält man Aussagen über die möglichen Phasenfaktoren exp if.
		Das ist aber noch nicht so spannend. Denn bisher haben wir keinen Spin berücksichtigt. Wenn wir jetzt noch zulassen, daß die Teilchen einen Spin haben (und wir im Detektor den Spin messen), könnten wir vielleicht die diversen Möglichkeiten doch unterscheiden.
	Könnten wir, aber wir können das Spielchen jetzt auch noch erweitern. Schauen wir uns den Stoß zwischen zwei Elektronen jetzt nochmal an:
		Wir könnten jetzt viele Prinzipbilder malen: Erstes Elektron mit Spin "Up", zweites Elektron mit Spin "Down" - und umgekehrt. Wir erwarten bei Vertauschung von Elektron 1 und 2 natürlich keinen Unterschied im Ausgang des Experiments. Dann haben wir noch die Möglichkeit, daß beide Spin "up", oder beide Spin "down" haben.
		Wenn man alle Möglichkeiten durchdekliniert, wird es langsam eng für die Möglichkeiten, die für den Phasenfaktor noch bleiben. So eng, daß in voller Allgemeinheit (für alle möglichen Teilchen mit allem möglichen Spins) nur noch zwei Phasenfaktoren übrig bleiben:
		exp if  =  {   + 1   Bose Teilchen – 1   Fermi Teilchen
	Mutter Natur hat nun aus Gründen die nur sie kennt, beide der logisch möglichen Fälle realisiert. Das Pluszeichen gilt für alle Bosonen, also Teilchen mit ganzzahligem Spin, das Minuszeichen für alle Fermionen, also Teilchen mit halbzahligem Spin.
	Man kann das ganze noch etwas "anschaulicher" darstellen. Der entscheidende Gedanke bei den hypothetischen Streuexperimente war, daß man alle möglichen Parameter in der Ausgangssituation austauschen kann, ohne daß sich am Ergebnis etwas ändern darf.
		Das bedeutet, daß wenn man in einer der relevanten Wellenfunktionen bei den Variablen welche "tauscht", z.B. die Positionsvektoren der beiden Teilchen oder ihre Spinrichtung, wird aus der alten Wellenfunktion y(vor Vertauschung) eine neue Wellenfunktion y(nach Vertauschung), und diese Operation läuft immer nach folgendem Muster ab:
		y(nach Vertauschung)  =  {      y(vor Vertauschung)   Bose Teilchen – y(vor Vertauschung)   Fermi Teilchen
	Haben wir damit das Pauli-Prinzip erklärt?
		Haben wir natürlich nicht. Wir haben es nur anders formuliert. Wir haben zwar verstanden, daß für ununterscheidbare Teilchen prinzipiell zwei Möglichkeiten existieren, wie sie sich bei Interaktionen verhalten können.
		Warum sie sich je nach Halb- oder Ganzzahligkeit ihres Spins für jeweils eine der beiden Möglichkeiten entscheiden - das ist aber immer noch völlig unklar und keine unmittelbare Konsequenz aus anderen tiefen Prinzipien.

Mit Frame

2.1.5 Loesungen der Schroedingergleichung und Aufbau aller Atome

Feynman und Pauli-Prinzip

© H. Föll (MaWi 1 Skript)