 |
Als Regel kann man formulieren: |
|
 |
Atome "wollen gerne"
gefüllte Orbitale (oder "Schalen") haben. |
|
 |
Etwas präziser ausgedrückt: Bei gefüllten Orbitalen ist die Energie des Elektronensystems
minimal im Vergleich zu benachbarten Konfigurationen mit mehr oder weniger Elektronen. Dadurch besteht keine Tendenz zur
Veränderung, d.h. zu einer chemischen Reaktion. Denn: |
|
|
|
|
 |
Es ist wichtig sich dabei klarzumachen, daß die Energie der Elektronen eines Atoms mit
der Schrödingergleichung im Prinzip berechnet werden kann (und wird). Daß
wir es in der Realität (noch) nicht können, macht nichts. Jedenfalls steckt
in der obigen Regel kein Geheimnis mehr, sondern sie beschreibt nur eine offenkundige (qualitative) Lösung der Schrödingergleichung. |
 |
Eine erste Schlußfolgerung wird möglich. |
|
 |
Wenn ein einzelnes Atom keine gefüllten Orbitale
hat, das Ideal minimaler Energie also nicht erreicht, könnte es Elektronen abgeben
oder aufnehmen um als "zweitbeste" Lösung doch noch gefüllte Orbitale
zu bekommen. Dazu braucht es aber Partner, die sein überschüssiges Elektron aufnehmen oder ihm eines abgeben. |
|
 |
Wir stellen also die Frage, ob Partnerschaft zwischen Atomen, ob chemische
Bindung, als zweitbeste Lösung in Fragen kommt, wenn "splendid isolation" energetisch nicht günstig
ist. |
|
 |
Sind also Elemente, die ein Elektron zuviel haben oder zuwenig haben - die Alkalimetalle
bzw. Halogene - geeignete Partner für enge Bindungen? |
 |
Die Antwort ist, wir wissen es, ein emphatisches Ja!
Alkaliatome und Halogenatome formen gern und oft viele und sehr stabile Verbindungen; z.B. das für uns so wichtige
Kochsalz: NaCl. Aber auch andere häufige und wichtige "Salze" wie z.B.
LiF, LiCl, KCl, KBr, KJ. |
 |
Aber nicht nur die besonders reaktiven Alkali- und Halogenatome, sondern auch
andere Atome gehen gerne Bindungen ein. Abgesehen von den Edelgasen tun es alle! |
|
 |
Manche so gerne, daß wir sie in Natur nie allein,
d.h. elementar finden, z.B. die Metalle Al, Ti, Fe; aber auch Si oder Ge. Sie alle sind
in der Regel oxidiert, d.h. als Verbindung mit Sauerstoff präsent. Andere sind
weniger reaktiv und kommen auch "gediegen", d.h. elementar vor: Au, Ag, Pt, Pd, Ir
(die Edelmetalle), aber auch z.B. Cu und S. Aber so ganz ohne Partner sind sie selbst dann nicht. Sie sind
lediglich homoerotisch und tun sich mit Atomen der eigenen Art zusammen, wie auch die Gase O2, N2,
Cl2, ... . |
 |
Partnerschaften, oder präziser gesagt, chemische Verbindungen
sind also die Regel. Da wir die Materialwissenschaft hier auf feste Körper beschränken wollen, die per definitionem
allesamt Verbindungen sind, müssen wir lernen, was Chemie, Physik, und insbesondere die Quantentheorie, an Kernaussagen dazu bereit halten.
|
|
 |
Dazu betrachten wir zunächst noch einige meßbare
Eigenschaften einzelner Atome, die aber bereits Aussagen über mögliche Bindungen
mit anderen Atomen implizit enthalten. Es sind dies die Größen: |
| |
|
 |
Um diese Begriffe kennenzulernen, betrachten wir den formalen
Weg zweier Atome aus ihrem isolierten Dasein in einem gebunden Zustand. Schauen wir uns dazu eine
mögliche Bindungsreaktion am einfachsten Beispiel, dem LiF genauer an. |
|
 |
Wir unterstellen, daß das Li sein überschüssiges Elektron an das F
abgibt (dem ein Elektron fehlt), und daß die beiden geladenen Atome (die dann Ionen heißen)
sich dadurch fest verbinden - das tun sie dann einfach über die elektrostatische Anziehung. Dabei muß
Energie frei werden, die Bindungsenergie, sonst würde der Prozeß
nicht von alleine (ohne äußeren Zwang, d.h. Energiezufuhr) ablaufen. Diesen Prozeß kann man in seine einzelnen
elementaren Schritte zerlegen, aus denen die Bindungsenergie berechnet werden kann. |
|
 |
Zunächst überführen wir ein Li-Atom
in ein Li-Ion, indem wir ihm ein Elektron wegnehmen. Dazu braucht man Energie;
von alleine wird es nicht geschehen. Wir schreiben die notwendige Reaktion: |
| |
|
|
 |
Das heißt in Worten: Einem (elektrisch neutralem) Li-Atom kann
durch die Zufuhr (+ Zeichen) von 5,4
Elektronenvolt Energie ein Elektron abgetrennt werden.
"Abgetrennt" heißt in der Idealwelt der physikalischen Mathematik, daß das Elektron gegen die elektrostatische
Anziehung des jetzt + geladenen Ions ins "Unendliche" gebracht wird; dazu muß man Arbeit verrichten. |
|
 |
Die Energieeinheit "Elektronenvolt" ist dem
Bereich des atomaren angemessen, es ist die Energie, die ein Elektron gewinnt, wenn es die Spannung von 1V durchläuft. |
 |
Die mehr chemisch geprägte Welt verwendet jedoch nach wie vor die Einheit
"kJ/mol". Die Umrechnung ist einfach, wir haben |
|
| 1 kJ/mol | = |
1.0365 · 10–2 eV |
| | | |
| 1 eV | = |
96.485 kJ/mol |
|
|
|
 |
Da es ein leicht faßlicher Gedanke ist, daß wir jedem Atom mit
Gewalt ein Elektron abtrennen können, ist die dafür notwendige Energie die erste
Materialkonstante, die wir kennenlernen. Sie heißt Ionisierungsenergie
I
und ist für jedes Atom definiert. |
|
 |
Die Ionisierungsenergie ist verhältnismäßig leicht meßbar, aber wir
behalten im Hinterkopf : Im Prinzip kann sie auch aus der Schrödingergleichung errechnet werden. Einige Werte finden
sich im Modul Ionisierungsenergien und Elektronegativität einiger Elemente. |
 |
Wie sieht es auf der Fluor Seite aus? Wir gehen am besten vom Wunschzustand aus:
Volle Schale heißt, daß ein weiteres Elektron dazu kommen muß. Die entsprechende Reaktion - aus Symmetriegründen
"rückwärts" geschrieben - lautet: |
|
|
|
|
 |
Das heißt in Worten: Einem (negativ geladenem)
Fluor-Ion kann durch die Zufuhr (+
Zeichen) von 3,6 eV Energie ein Elektron abgetrennt werden; dadurch entsteht ein elektrisch neutrales Fluor Atom.
So geschrieben ist die Reaktion immer möglich. |
|
 |
Schreibt man die Reaktion "vorwärts", lautet sie |
| |
|
|
 |
In Worten: Beim Anlagern (+
Zeichen) eines Elektrons an ein neutrales Fluor-Atom werden 3,6 eV Energie frei
(– Zeichen!) Diese freiwerdende Energie bei
Anlagerung eines Elektrons heißt Elektronenaffinität A.
|
|
 |
Wir haben aber jetzt ein Problem. Im Gegensatz zur Ionisierungsenergie ist
eine (positive) Elektronenaffinität nicht für
alle Atome definiert. Denn man kann zwar mit Gewalt jedem Atom ein Elektron wegnehmen, aber man kann Atome nicht zwingen
ein zusätzliches Elektron gebunden zu halten. |
|
 |
Formal, oder rein mathematisch gesehen, ist das kein Problem:
Die Elektronenaffinität wäre in diesem Falle eine negative Zahl und damit
keine Energie mehr die frei wird, sondern eine "Zwangsenergie". Da eine negative Elektronenaffinität aber
keinen besonderen Sinn ergibt, ist die Elektronenaffinität nur für Elemente definiert, die eine echte Affinität,
ausgedrückt in einer positiven Bindungsenergie zeigen. |
|
 |
Auch die Elektronenaffinität ist verhältnismäßig leicht meßbar,
kann aber im Prinzip auch aus der Schrödingergleichung errechnet werden. Einige Werte finden sich in der Tabelle Elektronenaffinitäten einiger Elemente |
 |
Ein weiterer Parameter, der die Neigung von Atomen zur Abgabe oder Aufnahmen von
Elektronen (d.h. die Neigung zur Ionisierung) beschreibt, soll kurz angesprochen werden, nämlich die Elektronegativität.
|
|
 |
Die Elektronegativität ist eine von dem großen Chemiker Linus Pauling eingeführte Energieskala, die in etwas unscharfer Weise angibt, wie sich zwei
Elemente ein Elektron teilen. Das elektronegativere Element zieht das Elektron stärker
an als das schwächere. Man kann mit dem Konzept der Elektronegativität auch Zweierbeziehungen beschreiben, bei
denen der Übergang eines Elektrons von einem Atom zum anderen nicht hundertprozentig erfolgt. |
|
 |
Einige Werte finden sich in der Tabelle Elektronegativitäten
einiger Elemente. |
|
 |
Wir erwähnen die Elektronegativität hier mehr aus historischen Interesse und weil
sie im Sprachgebrauch der Chemie noch sehr lebendig ist. In einem "advanced" modul gibt es noch Detailinformationen. |
 |
Wir haben jetzt quantitative Parameter die
uns etwas über Energien sagen. Damit können wir das Quantenzahlen-Energiediagramm
des vorhergehenden Unterkapitels jetzt "richtig", und nicht mehr nur schematisch darstellen. |
|
 |
Gedanklich müssen wir dazu aus jedem durch die Quantenzahlen gegebenen Zustand
das dort befindliche Elektron abtrennen und ins Unendliche bringen. Nimmt man dazu den energetisch höchsten besetzten
Zustand, erhält man die uns jetzt bekannte Ionisierungsenergie. |
|
 |
Im Gedankenversuch kann man das aber auch mit Elektronen machen die auf tieferen Niveaus sitzen,
"näher" am Atomkern. Auch für solche Elektronen ist eine eindeutige Energie definiert, die man messen
oder rechnen kann. |
|
 |
Man erhält beispielsweise für Li und Al die folgende Darstellung und einige weitere über den Link. |
| |
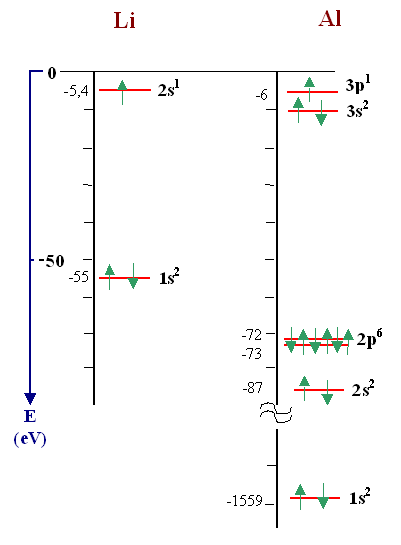 |
Die grünen Pfeile symbolisieren
die Elektronen; jeweils mit Spin "up" oder "down".
|
|
 |
Da wir wissen, daß Metalle viel freie Elektronen haben, die sich von den
Atomen gelöst haben müssen, Isolatoren dagegen keine, können wir uns schon hier leicht einige allgemeine
Regeln ableiten: |
|
 |
Elemente mit kleinen Ionisierungsenergien,
die also leicht Elektronen abgeben, sind i.a. Metalle. |
|
 |
Im Umkehrschluß: Metalle, wenn sie als Ionen vorliegen. sind i.a. positiv
geladen |
|
 |
Elemente mit positiven (d.h. überhaupt definierten)
Elektronenaffinitäten, die also zusätzliche Elektronen binden können,
sind i.a. Isolatoren. In ionischer Form sind sie negativ
geladen. |
|
 |
Elemente mit 3 ... 5 Elektronen in der äußersten Schale, die also gefüllte
Schalen durch Abgabe oder Aufnahme mehrerer Elektronen erhalten können, sind "unentschieden" |
|
 |
Beispiele dafür sind: C, Si, Ge, Sn, Bi - also auch die für uns besonders
wichtigen Elemente. |
| |
|
© H. Föll (MaWi 1 Skript)
