|
Man betrachte ein Teilchen mit der Energie E < E0,
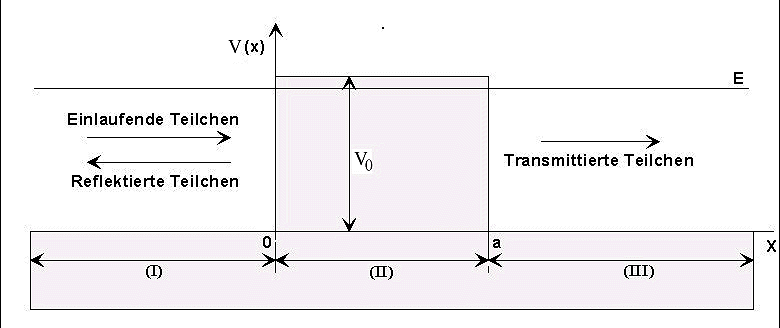
das sich in dem unten dargestellten Potential (Potentialbarriere) von links kommend bewegt. |
|
 |
Das ist schlicht eine erweiterte Form der Übungsaufgabe
2.1-5. |
|
 |
Das Potential ist definiert durch: V = 0 in Gebiet (I), V =
V0 in Gebiet (II) und V = 0in Gebiet (III) |
| |
|
 |
Fragen: |
|
 |
1. Wie verhält sich ein klassisches Teilchen in diesem Potential? |
 |
Es soll nun hergeleitet werden, wie sich das Teilchen verhält, wenn man es
quantenmechanisch beschreibt. Wie man bereits bei der Potentialstufe gesehen hat, sind
Teilchen in der Quantenmechanik in der Lage, etwas in klassisch verbotene Bereiche einzudringen. Daher muß man damit
rechnen, daß das Teilchen auch in das Gebiet hinter der Barriere dringen kann. |
|
 |
2. Wie lautet die Schrödinger-Gleichung eines Teilchens in Gebiet (I)?
|
|
 |
3. Man zeige, daß
y1(x) = A · exp( +ikx) + B · exp( –ikx)
eine Lösung der Schrödinger-Gleichung in Gebiet (I) ist. Dabei gilt k = (2mE)½/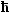 =
Wellenvektor. =
Wellenvektor. |
|
 |
4. Die Schrödinger-Gleichung in Gebiet (II)
lautet |
|
|
¶2y2
¶x2 | + |
2m
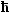 2 2 |
· (E – V0) · y2 =
0 |
|
|
|
 |
Eine allgemeine Lösung dieser Gleichung ist:
y2(x) = C · exp –(k ·
x) + D ·exp +(k · x) .Welchen Wert nimmt der Wellenvektor k in diesem Gebiet an? |
|
 |
5. Die Lösung der Schrödinger-Gleichung in Gebiet (III) lautet:
y3(x) = F · exp +(ikx)
mit dem Wellenvektor
k = (2mE)½/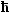
wie zuvor. |
|
 |
Warum macht eine Lösung der Form
y3(x) = F · exp –(ik ·
x) + G ·exp +(ik · x)
physikalisch keinen Sinn? |
|
 |
6.Um den Zusammenhang der Konstanten A, B, C, D und F
zu ermitteln muß man welche Bedingungen verwenden? |
|
 |
7. Für den hier betrachteten Fall eines von links einlaufenden Teilchens kann
man folgenden Zusammenhang zwischen den Konstanten A, B und F ermitteln: |
|
 |
A = F · cosh (2ka) + i ·d ·
2sinh(2ka) · exp(2ika)
und
B = -F · i h · 2sinh(2ka).
Dabei gilt:
d = k k – kk und
h = kk + kk. |
| | |
© H. Föll (MaWi 1 Skript)