 |
Wir betrachten ein Teilchen, das sich in dem dargestellten Potential eindimensional
bewegt. Das Teilchen habe eine Gesamtenergie E, für die gelten soll: E < V0.
|
|
 |
Das ist eine wichtige Beschränkung! Ein klassisches
Teilchen kann sich deshalb nur im Bereich (1) aufhalten. Wenn das nicht glasklar
ist, unbedingt darüber nachdenken! |
|
 |
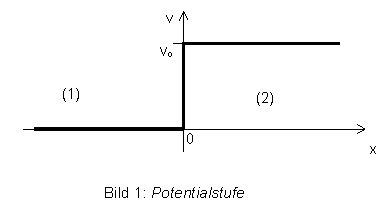
Die Potentialstufe sieht also so aus: |
| |
|
|
 |
Links ist das Potential - also die potentielle Energie des Teilchens - Null, rechts hat es
den endlichen Wert V0 |
|
 |
Wir fragen uns im wesentlichen, was einem Teilchen passiert das sich im Bereich (1)
aufhält, wenn es auf die Potentialschwelle trifft. |
| |
| |
 |
Fragen: |
|
 |
1. Wie lautet die Schrödinger-Gleichung für das Teilchen in Gebiet (1)? |
|
 |
2. Zeige, daß y1(x) = A
· exp (ikx) + B · exp –(ikx) eine Lösung der Schrödinger-Gleichung in
Gebiet (1) ist.
A und B sind von 0 verschiedene Konstanten, und i ist die imaginäre Einheit;
i2 = –1. |
|
 |
Was wird durch k physikalisch beschrieben? Hinweis:
Beachte die Dimension und die allgemeine Form der Lösung (verwende den Eulerschen Satz). |
|
 |
3. Wie lautet die Schrödinger-Gleichung für das Teilchen in Gebiet (2)? |
|
 |
4. Zeige, daß y2(x) = C
· exp –(a · x) eine Lösung der Schrödinger-Gleichung in
Gebiet (2) ist.
C ist wieder eine von null verschiedene Konstante. |
|
 |
Weiterhin gilt: |
|
|
| a2 = |
2m · (V0 – E)
|
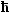 2 2 |
|
|
|
 |
5. Berechne die Aufenthaltswahrscheinlichkeit
|y2(x)|2 des Teilchens in Gebiet (2) und vergleiche
das Ergebnis mit deiner Erwartung für ein klassisches (nicht quantenmechanisches)
Teilchen? |
|
 |
6. Was könnte passieren, wenn statt einer Potentialschwelle eine dünne Barriere
genommen wird? |
|
 |
7. Warum macht die Lösung y1'(x)
= C' · exp –a · x für Gebiet (1) physikalisch keinen
Sinn? |
|
 |
8. Welcher Grenzfall führt bei diesem Problem auf das klassische Ergebnis? |
| |
|
© H. Föll (MaWi 1 Skript)
![]() 2.1.3 Schroedingergleichung und Wasserstoffatom
2.1.3 Schroedingergleichung und Wasserstoffatom