 |
In der klassischen Physik,
aber auch in der Elektrotechnik oder Materialwissenschaft, wird oft mit komplexen Zahlen
gerechnet, obwohl alle berechneten (und letztlich auch immer meßbaren) Größen immer reell sind.
|
|
 |
Es gibt in der klassischen Physik keine imaginären
Energien, Orte, Zeiten, Spannungen, Ströme usw.! Die Einführung komplexer Größen dient nur
der Bequemlichkeit beim Rechnen. Im Endergebnis treten nur reelle Zahlen auf - im Zweifel nimmt man vom Ergebnis nur den
Realteil oder den Imaginärteil. |
 |
In der Quantenmechanik ist das anders. Die konventionellen
meßbaren Größen, die zwar letztlich immer als Endergebnis erscheinen,
sind zwar auch immer reell, aber die Wellenfunktion
selbst, manchmal auch die Zeit, ist oft eine intrinsisch komplexe
Zahl. |
|
 |
Das ist schwer zu akzeptieren, aber das waren die irrationalen Zahlen auch. Pythagoras ließ einen seiner Schüler, der behauptete, daß es irrationale
Zahlen wirklich gäbe, sogar hinrichten (heute ist es viel ungefährlicher,
seinem Professor zu widersprechen). |
 |
Obwohl komplexe Zahlen oft mit dem berühmten Mathematiker Gauss
assoziiert werden, ist ihre Geschichte etwas älter. Insbesondere war Gerolama Cardano von großer Bedeutung . Er ist heute fast schon vergessen, seine Biographie
aber ist so interessant, daß es sich lohnt sie kurz darzustellen. |
 |
Diese Seite wird die wesentlichsten Grundlagen der komplexen Zahlen und ihre Nützlichkeit
bei einigen Fragestellungen der klassischen Physik wiederholen. Die wichtigsten Stichworte dazu sind |
|  |
Definition und Eigenschaften komplexer Zahlen; Gaußsche Zahlenebene. |
|
 |
Eulersche Beziehung. |
|
 |
Einfache Beispiele zur Nützlichkeit der komplexen Zahlen. |
|  |
Ausblick auf komplexe Funktionen. |
 | |
Weiterführende Informationen finden Sie auch in einem reinen Mathematik-Skript |
 |
Real- und Imaginärteil |
|  |
Komplexe Zahlen sind Zahlen der Form z = x + iy wobei x
und y reelle Zahlen sind. Die komplexen Zahlen stellen eine Erweiterung der reellen Zahlenmenge dar.
|
|
 |
Die imaginäre Einheit i genügt der Gleichung i2
= –1. Daher gilt für die imaginäre Einheit i = (–1)½. |
|
 |
Ist z = x + iy, so ist Re(z) = x der Realteil und Im(z) = y der Imaginärteil
der komplexen Zahl z. |
|
 |
Achtung: Nicht iy ist
der Imaginärteil der komplexen Zahl z, sondern nur die reelle Zahl
y. |
| |
 |
Zahlenebene |
|
 |
Eine komplexe Zahl z = x + iy läßt sich in der Gaußschen Zahlenebene durch einen Punkt P darstellen. Hierzu faßt man den Real-
und den Imaginärteil der komplexen Zahl z = x + iy als kartesische
Koordinaten des Punktes P in der x,y-Ebene auf. |
| |
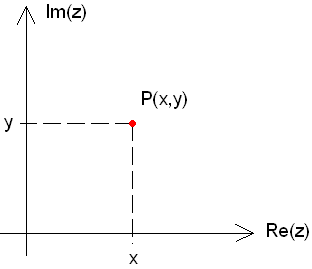
Darstellung einer komplexen Zahl durch einen Punkt
in der Gaußschen Zahlenebene |
|
|
 |
In den Anwendungen werden komplexe Zahlen meist durch sog. Zeiger
dargestellt. Dabei handelt es sich um einen Pfeil, der vom Ursprung des Koordinatensystems
zum Bildpunkt P(z) gerichtet ist. |
|
 |
Zeiger werden oft durch Unterstreichen gekennzeichnet: z
= x + iy. Das führt aber zur Verwechslungsgefahr mit Vektoren, die zumindest in HTML auch durch unterstreichen
dargestellt werden - und Zeiger sind zwar Pfeile, aber keine Vektoren! |
|
|
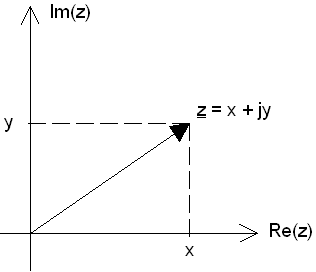
Darstellung einer komplexen Zahl durch einen Zeiger
in der Gaußschen Zahlenebene. |
| Hier ist zur Abwechslung mal das In der Elektrotechnik gebräuchliche
Symbol j für die imaginäre Einheit gezeigt. |
|
|
 |
Achtung: Der Zeiger z ist eine geometrische Darstellung
der komplexen Zahl z und nicht mit einem Vektor zu verwechseln! |
| |
 |
Konjugiert komplexe Zahlen; Betrag oder Modulus |
|  |
Die komplexe Zahl z* = x –
iy ist die zu z = x + iy
konjugiert komplexe Zahl. |
|
 |
Die zu einer komplexen Zahl konjugiert komplexe Zahl erhält man durch einen Vorzeichenwechsel
im Imaginärteil von z, während der Realteil unverändert bleibt: |
|
 |
Re(z*) = Re(z) und Im(z*) = – Im(z)
|
 |
Die Entstehung der konjugiert komplexe Zahl z* läßt sich
in der Gaußschen Zahlenebene durch Spiegelung der komplexen Zahl z
an der reellen Achse veranschaulichen. |
| |
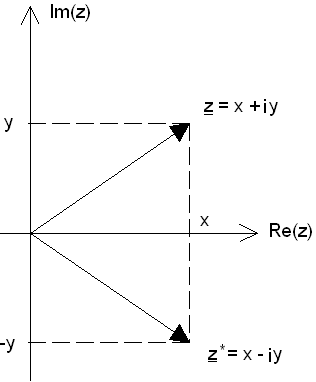
Komplexe Zahl und die zu ihr konjugiert komplexe Zahl
in der Gaußschen Zahlenebene
|
|
|
 |
Unter dem Betrag
|z| der komplexen Zahl z = x + iy versteht man die Länge
des zugehörigen Zeigers in der Gaußschen Zahlenebene: |
|
|
|
|
 |
Statt Betrag sagt man auch Absolutbetrag
oder Modul. |
| | |
 |
Die Eulersche Beziehung ist eine der wichtigsten und merkwürdigsten Gleichungen der Mathematik.
Sie verkoppelt 5 der wichtigsten Zahlen die es gibt, nämlich 0, 1, i, p und
e! Mehr darüber findet sich in spannender Form in den Feynman Lectures.
Wir brauchen sie für alternative Darstellungen komplexer Zahlen. |
|
 |
Die Form z = x + iy bezeichnet man als Gaußsche oder kartesische Darstellung
einer komplexen Zahl. Daneben existieren noch zwei weitere Darstellungsformen: die trigonometrische
Form und die Eulersche Form.
|
|
 |
In der trigonometrischen Form wird eine komplexe Zahl über
ihre Polarkoordinaten
r und j festgelegt: |
| |
|
|
 |
Mit r Î [0, ¥], j
Î [p, –p]
|
|  |
Hierbei gilt: |
| |
| r | = | Betrag von z | | |
| | | j | = |
Argument, Winkel
oder Phase von z |
|
|
 |
Mit Hilfe der Transformationsgleichungen x = r · cosj
und y = r · sinj kann man eine komplexe Zahl aus der kartesischen Form in die trigonometrische
Form überführen. |
| |
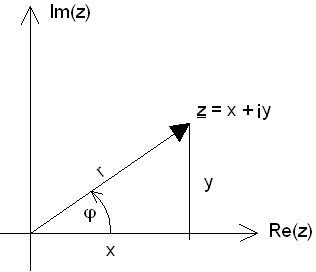
Veranschaulichung der trigonometrischen Form einer komplexen Zahl |
|
|
 |
Der Übergang von der komplexen Zahl z zu der konjugiert komplexen Zahl z*
entspricht in der trigonometrischen Darstellung einem Vorzeichenwechsel im Argument j
während der Betrag der komplexen Zahl konstant bleibt:. |
| |
| z | = |
r · (cosj + i · sinj)
| | | | |
| z* | = |
r · ( cos –j + i · sin –j) | | | |
| | = |
r · (cosj – i · sinj) |
|
|
|
 |
Verwendet man die von Euler stammende Formel |
| |
|
|
 |
so erhält man aus der trigonometrischen Form die Eulersche
Form einer komplexen Zahl: |
| |
|
|
 |
Diese Schreibweise einer komplexen Zahl ist besonders vorteilhaft beim Ausführen von Multiplikationen und Divisionen. |
|  |
Die zu z = r·eij gehörende konjugiert komplexe
Zahl z* lautet in Eulerscher Form |
| |
| z* | = |
[r · eij]* = r · e–
ij |
|
|
 |
Addition, Subtraktion, Multiplikation und Divison
von komplexen Zahlen in verschiedenen Darstellungsformen: |
 |
Addition und Subtraktion
komplexer Zahlen in kartesischer Form: |
|
 |
Komplexe Zahlen können nur in kartesischer Form addiert/subtrahiert
werden. Dies geschieht indem man ihre Realteile addiert/subtrahiert und ihre Imaginärteile
addiert/subtrahiert. |
| |
| z1 + z2 | = |
(x1 + iy1) + (x2 + iy2)
= (x1 + x2) + i · (y1
+ y2) | | | | |
| z1 – z2 | = |
(x1 + iy1) – (x2 + iy2)
= (x1 – x2) + i · (y1
– y2) |
|
|
 |
Multiplikation, Division und Potenzen komplexer Zahlen
|
 |
Multiplikation in kartesischer Form
|
 |
Es gelten die üblichen Multiplikationsregeln für Klammerausdrücke; danach muß
nach Real- und Imaginärteil sortiert werden: |
| |
| z1 · z2 | = |
(x1 + iy1) · (x2 + iy2) = (x1x2
– y1
y2) + i (x1y2 + x2
y1) |
|
|
 |
Multiplikation in trigonometrischer Form |
|
 |
Für die Ausführung von Multiplikationen erweist sich die trigonometrische Form oft als vorteilhafter
als die kartesischer Form. Die sture Durchmultiplikation ergibt zunächst |
|
|
| z1 · z2 | = |
r1 · (cosj1 + i sinj1)
· r2 · (cosj2 + i sinj2)
| | | | | | | = |
(r1 · r2) · [(cos(j1 + j2) + i · sin(j1 + j2)] |
|
|
|
 |
Dies läßt sich zusammenfassen zu einem klaren Bildunggesetz : |
| |
| z1 · z2 | = | z |
= |
r1 · eij1 · r2
· eij2 | | |
| | | | | | |
= |
(r1 · r2) · ei · (j1 + j2) |
|
|
 |
Division komplexer Zahlen in kartesischer
Form: Mühsam, aber klar. |
| |
z1
z2 | = |
x1 + iy1
x2 + iy2 | = |
x1x2+ y1 y2
x22 + y22 | + |
i · (x2 · y1 – x1 · y2)
x22 + y22 |
|
|
|
 |
Division komplexer Zahlen in trigonometrischer
Form ist einfach und elegant. |
| |
z1
z2 | = |
r1 · (cosj1 + i sinj1)
r2 · (cosj2 + i sinj2) |
= | r1
r2 |
· [(cos(j1 – j2)
+ i · sin(j1 –j2)] |
z1
z2 | = |
r1 · eij1
r2 · eij2 |
= | r1
r2 |
· ei(j1 –j2) |
|
|
|
 |
Potenzen
und Wurzeln einer komplexen Zahl. |
|
 |
Wendet man die Potenzgesetze auf z = r · eij
an, so erhält man die Moivre-Formel, welche angibt, wie man die n-te Potenz
einer komplexen Zahl berechnet: |
| |
| zn | = |
rn · ei n · j |
= |
rn · (cos n · j + i sin n ·
j) |
|
|
|
 |
Aus der Moivre-Formel läßt sich außerdem eine Formel zum Berechnen der n-ten
Wurzel einer komplexen Zahl herleiten. z hat genau n verschiedene n-te
Wurzeln w0 bis wn–1, die folgender Gleichung genügen |
| |
| wk | = | r1/n · |
æ
ç
è | cos |
j + 2kp
n | + |
i · sin | j + 2kp
n | ö
÷
ø |
|
|
 |
Natürlicher Logarithmus
einer komplexen Zahl. |
|
 |
Um den natürlichen Logarithmus einer komplexen Zahl berechnen zu können, ist es von Vorteil von der (erweiterten)
Exponentialform z = r · ei · (j + 2k · p)
der komplexen Zahl auszugehen, also eine "Phase" einzubauen. Daraus folgt |
| |
| ln z | = |
ln [r · ei(j + 2k · p)]
| | | | | |
= |
ln r + ln ei(j + 2k ·p) |
| | | | = |
ln r + i · (j + 2k · p) |
|
|
 |
Zunächst brauchen wir die Darstellung sinusförmiger
Schwingungen mit Hilfe komplexer Zeiger |
|
 |
y(t) = A · sin(wt
+ j) beschreibt eine sich mit der Zeit sinusförmig verändernde Größe
(Schwingung).
|
|
 |
Dabei ist A ist die Schwingungsamplitude, w =
2pf die Kreisfrequenz und j die Phase oder der Nullphasenwinkel. |
|
 |
Die harmonische Schwingung y(t) läßt sich durch einen komplexen
Zeiger in der Gaußschen Zahlenebene darstellen. Der komplexe Zeiger besitzt die Länge A und rotiert
im mathematisch positiven Drehsinn mit der Winkelgeschwindigkeit w um den Ursprung des
Koordinatensystems. |
| |
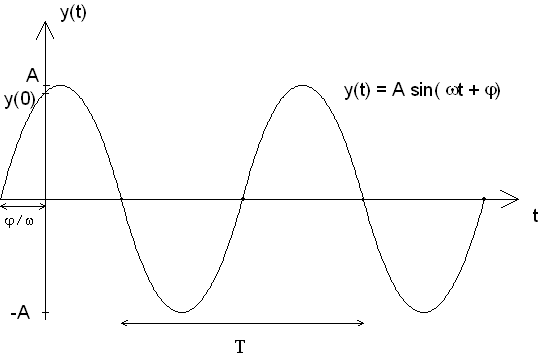
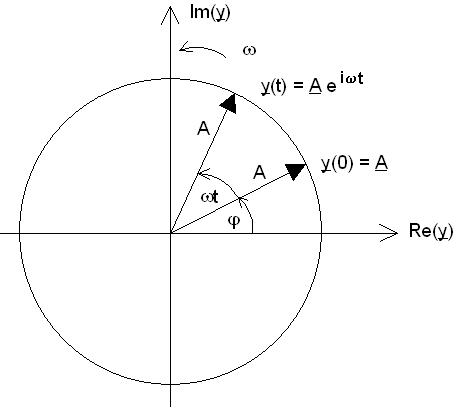
Darstellung eines harmonischen Schwingers durch einen rotierenden Zeiger |
|
|
 |
Zum Zeitpunkt t = 0 schließt der Zeiger y mit der
Bezugsachse (positive reelle Achse) den Nullphasenwinkel j ein. |
|
 |
In der Zeit t überstreicht der Zeiger den Winkel wt.
Die Lage des Winkels in der Gaußschen Zahlenebene läßt sich durch die zeitabhängige komplexe Zahl darstellen:
|
| |
| y | = |
A · [ cos(wt + j) + i ·
sin(wt +j)] | | |
| | | = |
A · eij · eiwt |
| | | | | = |
A · eiwt |
|
|
|
 |
Dabei ist |
|
|
| A = A·eij |
komplexe Amplitude (zeitunabhängig) |
| eiwt | Zeitfunktion |
|
|
 |
Die komplexe AmplitudeA ist zeitunabhängig; sie hat den Betrag |A|
= A und den Phasenwinkel j, welcher den Anfangswinkel des Zeigers festlegt.
|
|
 |
Die Zeitfunktion eiwt beschreibt
die Rotation des Zeigers mit der Winkelgeschwindigkeit w . |
|
 |
Der Imaginärteil des rotierenden Zeigers y entspricht dem Momentanwert der Sinusschwingung y(t) und damit der Projektion des Zeigers
auf die Imaginärachse zum Zeitpunkt t. |
|
|
| y(t) | = |
Im[A · eiwt] = A · sin(wt + j) |
|
|
 |
Die Überlagerung zweier gleichfrequenter Sinusschwingungen
in komplexer Darstellung zeigt nun wie praktisch diese Betrachtungsweise ist: |
|
 |
Gegeben sind zwei Schwingungen gleicher Frequenz aber verschiedener Phase |
| |
| y1 | = |
A1 · sin(wt +j1)
| | | | |
| y2 | |
A2 · sin(wt + j2) |
|
|
|
 |
Die ungestörte Überlagerung dieser Schwingungen ergibt nach dem Superpositionsprinzip
eine Schwingung y gleicher Frequenz, aber mit zunächst unklarer Amplitude und Phase, d.h. y = y1
+ y2 = A? · sin(wt +?). |
 |
Man kann das natürlich mit den trigonometrischen Funktionen ausführen,
aber die Amplitude A und die Phase ? der resultierenden Schwingung berechnet
man weit einfacher in komplexer Schreibweise als mit sin und cos Funktionen - insbsondere wenn wir mehr als
zwie Schwingungen überlagern. |
|
 |
Dazu stellt man die Schwingungen y1 und y2
durch komplexe Zeiger dar: |
| |
| y1 | ® |
y1 = A1 · eiwt |
| | | | | y2 |
® |
y2 = A2 · eiwt |
|
|
|
 |
Für die komplexen Schwingungsamplituden A1 und A2
gilt: |
| |
| A1 | = |
A1 · eij1 |
| | | | | A2 |
= |
A2 · eij2 |
|
|
|
 |
Anschließend überlagert man die komplexen Einzelschwingungen y1
und y2 durch schlichte Addition. Es folgt für y:
|
| |
| y | = |
A1 · eiwt + A2
· eiwt | | | |
| | = |
(A1 + A2) · eiwt |
| | | | | = |
A · eiwt |
|
|
|
 |
Für die resultierende komplexe Amplitude gilt daher |
| |
|
|
 |
Die gesuchte Schwingung (der zeitabhängige Teil)
y entspricht dem Imaginärteil der berechneten komplexen Schwingung y. Daher gilt: |
| |
| y | = |
Im(y) = Im(A · eiwt)
| | | | | | =
| A · sin(wt). |
|
|
 |
Das war eine einfache Überlagerung zweier Schwingungen. Es ist einleuchtend,
daß bei komplizierteren Problemen die komplexe Darstellung enorme Vorteile hat. |
| |
 |
Schwingkreise in der Elektrotechnik |
|
 |
In der Wechselstromtechnik geht man von sinusförmigen Strom- und Spannungsverläufen
aus. Daher ist es möglich, Stom und Spannung als komplexe Zeiger in der Gaußschen Ebene zu betrachten |
| |
| u | = |
2½ · U · ejwt |
| | | | | i | = |
2½ · I · ejwt |
|
|
|
 |
Den Quotienten aus der komplexen Spannung u und dem komplexen Strom i
(Achtung! Hierist, wie in der Elektrotechnik üblich i = Strom und j = (–1)½)
bezeichnet man als Impedanzoder Scheinwiderstand
Z |
| |
|
|
 |
Für einen (ohmschen) Widerstand R gilt: u = R·i.
Daher besitzt ein ohmscher Widerstand die reelle Impedanz ZR
= R. |
|
 |
Für eine Kapazität
C gilt der folgende Zusammenhang zwischen Strom und Spannung: |
| |
|
|
 |
Damit erhält man für die Impedanz der Kapazität
C folgenden Wert |
| |
|
|
 |
Aus dem Induktionsgesetz erhält man folgenden Zusammenhang zwischen u
und i für eine Induktivität L. |
| |
|
|
 |
Daraus ergibt sich folgende rein imaginäre Impedanz
Z L für die Induktivität |
|
|
|
 |
Mit Hilfe dieser Impedanzen lassen sich Wechselstromkreise einfach
berechnen. Dazu betrachten wir als Beispiel folgenden Reihenschwingkreis aus einem Widerstand R, einer Induktivität
L und einer Kapazität C: |
|
|

RLC-Reihenschwingkreis
|
|
|
 |
Nach den Kirchhoffschen Regeln erhält man die Gesamtimpedanz Z
des Wechselstromkreises durch Addition der Impedanzen der drei Bauteile
|
| |
| Z | = |
R + j · w · L + |
1
j · w · C | = |
R + j · | æ
ç
è |
w · L – | 1
w · C | ö
÷
ø
|
|
|
|
 |
Die folgende Abbildung zeigt die Lage der Gesamtimpedanz
Z im Zeigerdiagramm, die sich aus der graphischen Addition der einzelnen Zeiger
ergibt: |
| |
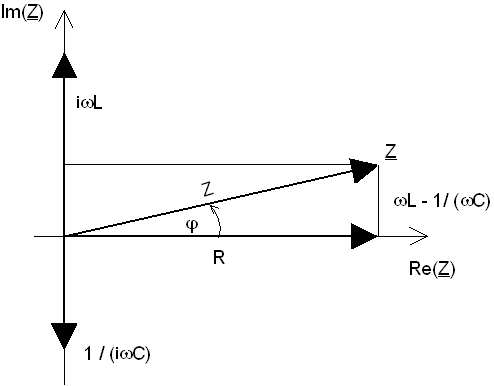
Zeigerdiagramm des Wechselstromkreises in Reihenschaltung |
|
|
 |
Der Wirkwiderstand der Reihenschaltung ist der Realteil der Impedanz Z ; Re (Z ) = R.
|
|
 |
Der Blindwiderstand der Reihenschaltung ist der Imaginärteil
der Impedanz Z ; Im (Z
) = wL – 1/wC. |
|
 |
Der reelle Scheinwiderstand
Z ist der Betrag des komplexen Vektors Z.
Die Phasenverschiebung j
= j u - j
i zwischen Spannung und Strom läßt sich berechnen zu |
| |
| j | = arctan | X
R
| = arctan | æ
ç
è |
w · L – 1/wC
R | ö
÷
ø |
|
|
|
 |
Das Verhältnis von Z L zu Z C
bestimmt die Größe von j und damit ob der Strom der Spannung nacheilt, ob die
Spannung dem Strom nacheilt oder ob im Resonanzfall Strom und Spannung in Phase sind. |
| | |
 |
Hat man erst mal komplexe Zahlen mit all ihren Darstellungsarten und Rechenregeln,
lassen sich natürlich jetzt auch Funktionen mit komplexen Variablen definieren. |
|
 |
Damit ist ein großes und (auch für die Materialwissenschaft) sehr
wichtiges Gebiet der Mathematik definiert, die Funktionentheorie. |
|
 |
Es ergeben sich völlig neue und wunderbare Beziehungen, eine davon wollen wir uns mal
genauer anschauen. Dazu betrachten wir die Lösungen der Poisson Gleichung, der Grundgleichung der Elektrostatik, die uns in der
Halbleiterei laufend begegnen wird. |
 |
Die Poisson-Gleichung der Elektrostatik lautet: |
|
|
| DF(x,y,z) |
= – | r(x,y,z)
ee0 |
|
|
|
 |
Mit D = Delta operator (¶2/¶x2 +¶2/¶y2
+ ¶2/¶z2), F(x,y,z)
= elektrostatisches Potential, r(x,y,z) = Ladungsverteilung im Raum |
|
 |
In zwei Dimensionen ist die Poissongleichung ein Spezialfall
eines allgemeinen Typs von Differentialgleichungen der sehr häufig vorkommt: der Laplace
Gleichung |
|
|
|
|
 |
- immer unter der Bedingung, daß F die spezifischen
Randbedingungen erfüllt, auf irgendeiner Oberfläche konstant zu sein. Elektrostatisch heißt das z.B. einfach
nur, daß die Oberfläche eines Leiters eine Äquipotentialfläche sein muß. Die Laplace - Gleichung
ist damit eine typische Grundgleichung für viele Randwertprobleme. |
 |
Es gibt keinen einfachen Weg um die Laplace - Gleichung (zusammen mit der spezifischen
Randbedingung) zu lösen. Analytisch klappt es nur für relativ einfache Oberflächen. |
 |
Jezt betrachten wir mal eine beliebige komplexe
Funktion f(z) mit der komplexen Variablen z = x + iy (und i ist wieder die imaginäre Einheit).
|
|
 |
Zum Beispiel |
|
|
| f(z) | = | was immer
einem einfällt |
|
|
|
 |
Für das erste Beispiel haben wir ausgeschrieben
|
| |
|
|
 |
Setzen wir eine komplexe Zahl mit dem Wertepaar (x, y) ein, erhalten wir als
Funktionswert eine neue komplexe Zahl. |
 |
f(z) läßt sich also auch immer schreiben als
|
| |
| f(z) | = | U(x, y) + i · V(x, y) |
|
|
|
 |
d.h. analog zur Darstellung der komplexen Zahl als Summe aus einer Funktion U die von
zwei reellen Variablen x, y abhängt plus
i mal eine andere Funktion V, die ebenfalls von den reellen Variablen x, y abhängt. |
 |
Das ist natürlich verallgemeinerbar: Alle
komplexen Funktionen lassen sich so darstellen! |
|
 |
Wir können also eine beliebige uns bekannte oder auch nur schreibbare Funktion f(x)
nehmen, statt x die komplexe Zahl z substitutionieren, und - nach kürzerer oder länglicher
Rechnung - damit zwei reelle Funktionen generieren: U(x,y) und V(x,y). |
|
 |
Und nun zum Überraschungseffekt: |
|
 |
Jede dieser unendlich vielen Funktionen
U(x,y) und V(x,y) ist eine Lösung der Laplace Gleichung! |
|
 |
Wir wissen nur nicht, zu welchem konkreten Randwertproblem! |
 |
Den Beweis für diese Behauptung überlassen wir der Mathematik. Es sollte
aber klar geworden sein, daß Funktionen komplexer Variablen für Überraschungen gut sind. |
|
 |
Leicht verrückt: Wir kennen die Antwort - aber nicht die Frage! Wer das Kultbuch (so
in den neunziger Jahren) "The Hitchhikers Guide to the Galaxy"
von Douglas Adams (der in diesem Jahr (2001) gestorben ist)
gelesen hat, wird sich jetzt fragen, ob Adams die Funktionentheorie kannte, denn das Buch (genauer gesagt alle 4
Bücher der Trilogie(?)) dreht sich genau um diese Frage: |
|
 |
Die Antwort zu den letzten Fragen bezüglich des Leben, des Universums und überhaupt
und so, ist bekannt; sie lautet: 42. Nur die genaue Frage ist offen. |
| | |
© H. Föll (MaWi 1 Skript)
![]() 2.1.3 Schroedingergleichung und Wasserstoffatom
2.1.3 Schroedingergleichung und Wasserstoffatom