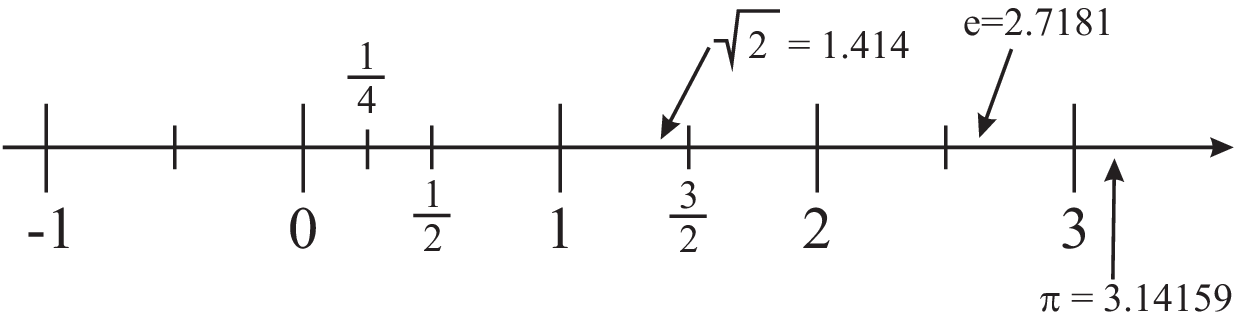2.1
Complex numbers: Definition
-
integers: \(\{\ldots,-3,-2,-1,\underbrace{0,\underbrace{1,2,3,\ldots}_{\mathbb{N}}}_{\mathbb{N}_0}\}=\mathbb{Z}\)
-
rational numbers: \(\mathbb{Q}=\frac{p}{q}\;\;
,\;p,\; q\in\mathbb{Z};\;\;q\notin0\)
-
real numbers: \(\mathbb{R}\)
\(\Longrightarrow\) real numbers are ”dense”
many equations have real numbers as solutions e.g.: as solutions e.g.: \begin{eqnarray*}
x^2-2=0&\Rightarrow&\;x_{1/2}=\pm\sqrt{2}\approx\pm1.41421\ldots\\ \sin x=0 &\Rightarrow&\;x=n\pi,\;\;n\in\mathbb{Z}\\ e^x-10=0&\Rightarrow&\;x=\ln10\approx2.302585\ldots
\end{eqnarray*}
But:
|
\[ \left.\begin{array}{ll}x^2+1=0&\Rightarrow x=?\\ e^x+10=0&\Rightarrow x=?\\\sin x=2&\Rightarrow x=?\end{array}\right\}\mbox{no
real numbers as solutions!} \] |
\(\Longrightarrow\) Definition of ”new” numbers!
-
complex numbers: \(\mathbb{C}\)
\(\Rightarrow\) almost all equations do have solutions in \(\mathbb{C}\) (even if they have no
real solution)
\(\Rightarrow\) simplification of calculations [complex \(e\)-function]
One new number is needed: \begin{eqnarray*} x^2+1=0&\Leftrightarrow&
x^2=-1\\ &\Leftrightarrow& x=\pm\underbrace{\sqrt{-1}}_i=\pm i \end{eqnarray*}
Definition 1
\(i\) is a number which square yields
\(-1\)
| \(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) | \(i^2=-1\) | \(\cdot\;\)only this number is enough
|
|
|
| \(\cdot\;\)\(i=\sqrt{-1}\)
not quite correct! |
\(\rightarrow\) all quadratic equations have now (always two!) simple solutions e.g.: \begin{eqnarray*} x^2+2x+10&=&0\\ \rightarrow x_{1/2}&=&-1\pm\sqrt{1-10}=-1\pm\sqrt{-9}=-1\pm\sqrt{-1\cdot9}\\&=&-1\pm3\sqrt{-1}=-1\pm3i
\end{eqnarray*}
Test:
| \[(-1+3i)^2+2(-1+3i)+10=1-9-6i-2+6i+10=0\] |
same for: \(-1-3i\)
\(\Rightarrow\) expressions
such as ”\(-1+3i\)” are solutions of equations\(\\\rightarrow\)”\(-1+3i\)”
is a new kind of number, a ”complex number”
\(i=\)”imaginary unit”
|
\[\underbrace{-1}_{\mbox{real part}}+\stackrel{\mbox{imaginary part}}{\overbrace{3}^{}i} \Rightarrow\mbox{A
complex number has a real and an imaginary part}\] |
|
\[\left.\begin{array}{lcl}\mbox{Re}(-1+3i)&=&-1\\\mbox{Im}(-1+3i)&=&3\end{array}\right\}-1+3i\] |
In general:
Definition 2
\(z=a+bi\;\;\in\mathbb{C},\;a,b\in\mathbb{R}\)
e.g. \(\;\;z_1=\sqrt{2}+5i,\;\;z_2=\frac{5}{3}+\sqrt{3}i\)
\(\Rightarrow\;\;\) complex numbers are
pairs of real numbers with \(i^2=-1\)
|
\[z=a+bi=(\underbrace{a}_{\mbox{\rm real}}\;,\underbrace{b}_{\mbox{\rm imaginary part}})= \underbrace{ \binom{a}{b}
=a \binom{1}{0}+b \binom{0}{1}}_{\mbox{\rm 2D Vector with two basic vectors}} \] |
Definition 3
\(\mbox{\rm Re}\{z\}=a,\;\;\;\mbox{\rm Im}\{z\}=b\)
© J. Carstensen (Math for MS)