Addition and Multiplication of complex numbers

2.2 Addition and Multiplication of complex numbers

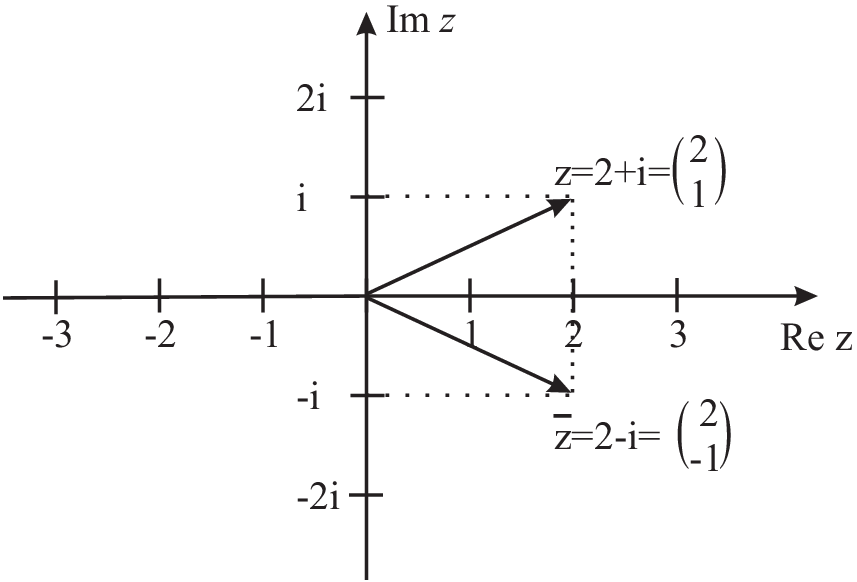
Definition 4

\[\begin{array}{c} z_1=a_1+b_1i\\z_2=a_2+b_2i \end{array}\Rightarrow\begin{array}{lcl}\oplus z_1+z_2&=&(a_1+a_2)+(b_1+b_2)i\\ \ominus z_1-z_2&=&z_1+(-z_2)=(a_1-a_2)+(b_1-b_2)i\\ \odot z_1\cdot z_2&=&(a_1+b_1i)(a_2+b_2i)=a_1a_2+b_1a_2i+a_1b_2i+b_1b_2i^2\\ &=&(a_1a_2-b_1b_2)+(a_1b_2+b_1a_2)i\end{array}\]

e.g.:

\[(3+2i)(1-i)=3-3i+2i+2=5-i\]

\begin{eqnarray*} (a+bi)+\overbrace{0}^{0+0i}&=&a+bi\\ (a+bi)\cdot \underbrace{1}_{1+0i}&=&a+bi \end{eqnarray*}

division: meaning of $\frac{1}{1+i}=?$

\[\Rightarrow \frac{1}{1+i}=\frac{1-i}{(1+i)(1-i)}=\frac{1-i}{2}=\frac{1}{2}-\frac{1}{2}i\;\;\;\mbox{o.k.}\]

In general:

\[\frac{1}{a+bi}=\frac{a-bi}{a^2+b^2}=\frac{a}{a^2+b^2}+\frac{-b}{a^2+b^2}i\]

\[z=a+bi\rightarrow z\cdot z^{-1}=1\Leftrightarrow z^{-1}=\frac{a}{a^2+b^2}+\frac{-b}{a^2+b^2}i\]

Definition 5 $\bar{z}=a-bi$ is the conjugate complex number to $z=a+bi$, other notation $\bar{z}=z^*$

Summary:

\[ \begin{array}{lcl} z&=&a+bi\\ \mbox{Re}(z)&=&a\\ \mbox{Im}(z)&=&b\\ \mbox{Re}(\bar{z})&=&a\\ \mbox{Im}(\bar{z})&=&-b \end{array}\Rightarrow \begin{array}{l} \mbox{Re}(z)=\frac{1}{2}(z+\bar{z})\\\\ \mbox{Im}(z)=\frac{1}{2i}(z-\bar{z})\\ \end{array} \]

Rules: $\quad\overline{\overline{z}}=z\;\;$, $\;\overline{z_1 + z_2}=\bar{z_1}+\bar{z_2}\;\;$, $\;\overline{z_1\cdot z_2}=\bar{z_1}\cdot\bar{z_2}$
”Normal” rules:

commutative law for addition and multiplication \begin{eqnarray*}z_1+z_2&=&z_2+z_1\\z_1z_2&=&z_2z_1\end{eqnarray*}
associative law $\oplus\odot$ \begin{eqnarray*}z_1+(z_2+z_3)&=&(z_1+z_2)+z_3\\ z_1(z_2z_3)&=&(z_1z_2)z_3\end{eqnarray*}
distributive law $z_1(z_2+z_3)=z_1z_2+z_1z_3$
neutral element

\[\begin{array}{cc}\oplus&0\\\odot&1\end{array}\]
unique solutions $z_1=v+z_2\;\;\;\Rightarrow\;\;\;(v=z_1-z_2)$
unique solutions $z_1=wz_2\;\;\;\Rightarrow\;\;\;(w=z_1/z_2)$
no ordering

order properties:$\;\;\;2\lt3,\;0\lt1\;\;$ o.k.
but $\;\;\;i\; {\genfrac{}{}{0pt}{}\gt\lt}\;0?$ \begin{eqnarray*} i\gt0\rightarrow i\cdot i&\gt&0\cdot i=0\rightarrow -1\gt0\quad\wr\\ i\lt0\rightarrow i\cdot i^3&\lt&0\cdot i^3=0\rightarrow 1\lt0\quad\wr \end{eqnarray*}

$\Rightarrow$ nonsense, complex numbers do not have order at all! (later we will discuss the modulus of z)
Gauß Plane of Numbers

$\Rightarrow$ complex numbers are 2D vectors with certain properties

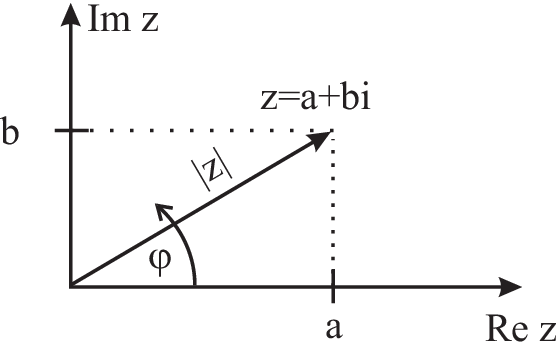
\begin{eqnarray*} \mbox{Modulus $r=|z|$ and phase $\varphi$} \qquad z&=&(r,\varphi),\\r&=&\sqrt{a^2+b^2},\;r=|z|=\sqrt{z\bar{z}},\\\varphi&=&\arctan\left(\frac{b}{a}\right)\rightarrow\varphi\;\mbox{in radians!!} \end{eqnarray*}

$z_1\;{\genfrac{}{}{0pt}{}\lt\gt}\;z_2\;\;$ makes no sense, but $|z_1|\;{\genfrac{}{}{0pt}{}\lt\gt}\;|z_2| $ is fine!
e.g.:$\;\;z_1=2+i=(\sqrt{5},\arctan(\frac{1}{2}))$ or $z_2=1+i=(\sqrt{2},\frac{\pi}{4})$
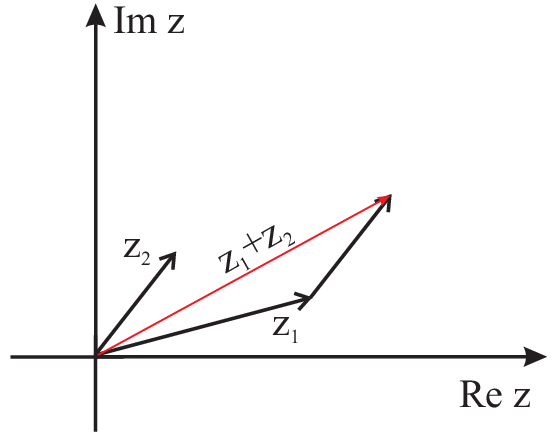
Geometrical interpretation of $+$ and $\cdot$ with complex numbers:

\begin{eqnarray*} \begin{array}{lcllcl} z_1&=&(r_1,\varphi_1)&z_2&=&(r_2,\varphi_2)\\ &=&a_1+b_1i& &=&a_2+b_2i\\ z_1+z_2&=&\mbox{''Adding 2D vectors''}\\ &&\left(\begin{array}{c}a_1+a_2\\b_1+b_2\end{array}\right)\\ z_1\cdot z_2 & = &(r_1r_2,\varphi_1+\varphi_2)\\ \end{array} \end{eqnarray*}

$\qquad \hat{=}$ Rotation and stretching of $z_1$ by $z_2$
$\qquad \Rightarrow$ see later
e.g.: $(1+i)(\frac{1}{2}+\frac{1}{2}i)=(\sqrt{2}\frac{1}{\sqrt{2}},\frac{\pi}{4}+\frac{\pi}{4})=(1,\frac{\pi}{2})=i$