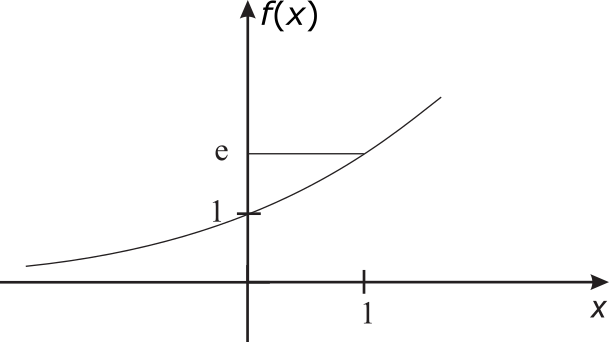
Function:\(f(x)=e^x,\;x\in\mathbb{R}\), \(\;\;\;\;e=2.7181\ldots\)

We define the exponential function as (the only non trivial function) which is it’s
own derivative:
Derivative of the exponential function:
| \[\frac{d e^x}{dx}= e^x \] |
Just using the definition of the factorial function we find the Taylor series expansion of the exponential function
| \[e^x=\lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n=\sum^\infty_{n=0}\frac{1}{n!}x^n\qquad\mbox{Euler's number: {\it e}}\] |
First we will prove some very important properties of the exponential function.
Fundamental addition formula of the exponential function:
Applying
the definition of the e-function as a series we find \begin{eqnarray*} e^x e^y&=&\sum^\infty_{n=0}\frac{x^n}{n!}
\sum^\infty_{m=0}\frac{y^m}{m!}\\ &=&\sum^\infty_{n=0} \sum^n_{k=0} \frac{x^ky^{n-k}}{k!(n-k)!}\\ &=&\sum^\infty_{n=0} \frac{1}{n!}\sum^n_{k=0}
\binom{n}{k} x^k y^{n-k}\\ &=&\sum^\infty_{n=0} \frac{(x+y)^n}{n!}\\ &=&e^{x+y} \end{eqnarray*}
Euler’s formula:
taking into account \(i^{4k}=1,\;\;\;i^{4k+1}=i,\;\;\;i^{4k+2}=-1,\;\;\;i^{4k+3}=-i\),
and using the definitions by the Taylor series we find \begin{eqnarray*} e^{i\varphi}&=&\sum^\infty_{n=0}\frac{(i\varphi)^n}{n!}=1+i\varphi+\frac{(i\varphi)^2}{2!}+\frac{(i\varphi)^3}{3!}+\frac{(i\varphi)^4}{4!}+\frac{(i\varphi)^5}{5!}+\ldots\\
&=&1-\frac{\varphi^2}{2!}+\frac{\varphi^4}{4!}+\ldots+i\left(\varphi-\frac{\varphi^3}{3!}+\frac{\varphi^5}{5!}-\ldots\right)\\
&:=&\cos\varphi+i\sin\varphi \end{eqnarray*}
This is a very important relation. It can be
understood as the definition of the sin and cos function and allows to replace \(\cos\varphi\) and \(\sin\varphi\)
by the (complex) e-function (and vice versa) \(\Rightarrow\) Simplification!!! (e.g. Waves \(\hat{=}\;\)complex
\(e\)-function). In addition the symmetries of the sin and cos functions get already obvious.
\(\sin x\) and \(\cos x\) vs. \(\exp\):
For real numbers \(\cos x\) and \(\sin x\) are just
the symmetric resp. antisymmetric representation of the \(\exp x\) function with the following properties
\begin{eqnarray*} e^{ix}&=&\cos x+i\sin x\qquad x \in\mathbb{R}\\ e^{-ix}&=&\cos x-i\sin
x\\ \\ &\Rightarrow& \begin{array}{ccl} \cos x&=&\frac{1}{2}\left(e^{ix}+e^{-ix}\right)\\\\ \sin x&=&\frac{1}{2i}\left(e^{ix}-e^{-ix}\right)\end{array}
\end{eqnarray*}
Additionally we directly get
| \[\cos^2x+\sin^2x = \left(\cos x + i \sin x \right) \left(\cos x - i \sin x \right) = e^{ix} e^{-ix} = 1\] |
Addition theorems for sin and cos functions:
Combining the exp-addition
formula with Euler’s formula we find \begin{eqnarray*} \left(\cos y \cos z -\sin
y \sin z \right)+i\left(\cos y \sin z +\sin y \cos z \right)&=&\\ \left( \cos y +i\sin y \right) \left( \cos z +i\sin z
\right)& = & e^{iy} e^{iz}\\ & = & e^{i(y+z)}\\ & = & \cos(y+z)+i\sin(y+z)\\ \end{eqnarray*}
From real and imaginary part we finally get (representing the even and odd part of the complex exponential function) \begin{eqnarray*} \cos y \cos z -\sin y \sin z & = & \cos(y+z)\\ \cos y \sin z +\sin y \cos z & = & \sin(y+z)\\ \end{eqnarray*}
Combining both equations we easily get
| \[\tan(y+z)=\frac{\tan(y)+\tan(z)}{1-\tan(y)\,\tan(z)}\] |
Back to complex numbers:
\(\rightarrow \qquad\)In general: |
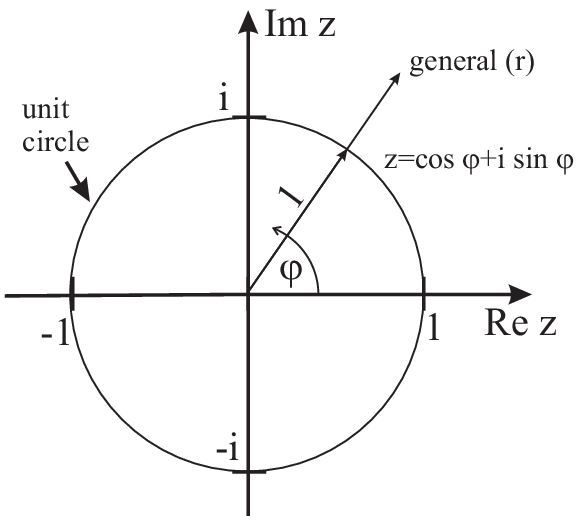 |
| \[f(z)=e^z\;\;\;z\in\mathbb{C} \mbox{ is the complex $e$-function with}\] |
| \[z=a+bi\;\Rightarrow\; e^{a+bi}=e^ae^{bi}=e^{a}(\cos b+i\sin b)\;\;\Rightarrow\mbox{complex $e$-function is periodical in }2\pi\] |
\begin{eqnarray*} \mbox{Re}(e^z)&=&e^{a}\cos b;\\ \mbox{Im}(e^z)&=&e^{a}\sin b;\\ b=0&\rightarrow&e^z=e^{a}\;\;\mbox{o.k.};\\ a=0&\rightarrow&e^z=e^{ib}=\cos b+i\sin b\;\;\mbox{o.k.}; \end{eqnarray*}
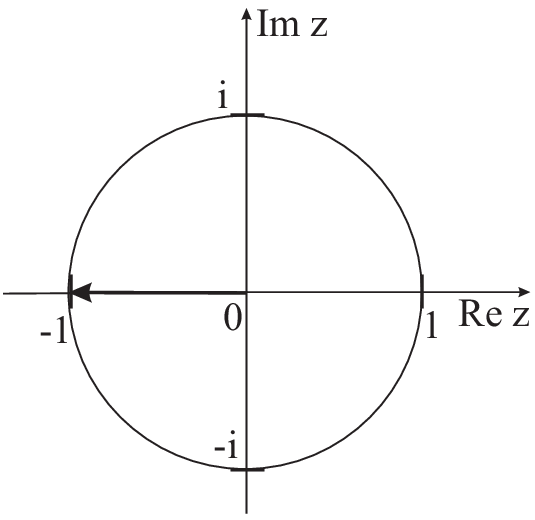
Example:
Has the equation \(e^z=-1\) any solution? (see
also 3.5)
\begin{eqnarray*} \mbox{z-real}\rightarrow \mbox{no}\\ \mbox{z-complex}\Rightarrow e^{a}\cos
b&=&-1\\ e^{a}\sin b&=&0\Rightarrow b=n\pi\\ &\Rightarrow&\underbrace{e^{a}}_{a=0}\underbrace{\cos n\pi}_{n=2k+1}=-1\\ &\Rightarrow&z=(2k+1)\pi
i\\ &\rightarrow&e^{\pi i}+1=0\;\;\mbox{beautiful expression} \end{eqnarray*}
| 
|
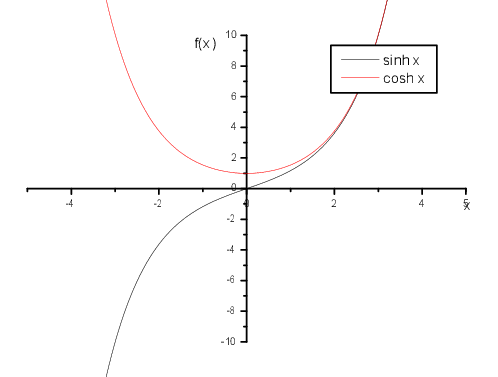
Similar to the definition of the cos and sin function we have
Definition 7
hyperbolic functions
\begin{eqnarray*}\cosh x&=&\frac{1}{2}\left(e^x+e^{-x}\right)\qquad\in\mathbb{R}\\ \sinh
x&=&\frac{1}{2}\left(e^x-e^{-x}\right)\\ \tanh x&=&\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}\end{eqnarray*}
| 
|
Theorem for \(\cosh\) and \(\sinh\):
| \[ \cosh^2x-\sinh^2x = \left(\cosh x + \sinh x \right) \left(\cosh x - \sinh x \right) = e^{x} e^{-x} = 1\] |
\(\rightarrow \sin z, \cos z \) for complex arguments are also defined in a logical way:
Definition 8
| \[\begin{array}{ccc}\sin z&=&\frac{1}{2i}\left(e^{iz}-e^{-iz}\right)\\\\\cos z&=&\frac{1}{2}\left(e^{iz}+e^{-iz}\right)\end{array}\qquad z\in\mathbb{C}\] |
e.g.: \begin{eqnarray*}\sin z=2&=&\frac{1}{2i}\left(e^{iz}-e^{-iz}\right)\\\Rightarrow4i&=&\underbrace{e^{iz}}_{w}-e^{-iz}\\ \Leftrightarrow w^2-4iw-1&=&0\\ \Rightarrow w_{1/2}&=&2i\pm\sqrt{5}i\\ w=e^{iz}&=&(2\pm\sqrt{5})i\\ \rightarrow\mbox{Re}(z)&=&0\rightarrow\cos b=0\rightarrow b=\left(n+\frac{1}{2}\right)\pi\\ \rightarrow \sin b&=&\pm1\\ \pm e^{a}&=&\left(2\pm\sqrt{5}\right)\\ a&=&\ln|2\pm\sqrt{5}|\\ \Rightarrow z&=&\ln|2\pm\sqrt{5}|+i\left(n+\frac{1}{2}\right)\pi\end{eqnarray*}
The above relation between sin, cos, sinh, and cosh allow e.g. to easily apply the addition theorems to calculate \begin{eqnarray*}\cosh\left( a + i b\right) & = & \cosh\left(a\right) \cosh\left(i b\right) + \sinh\left( a\right) \sinh\left( i b\right)\\ & = & \cosh\left( a\right) \cos\left( b\right) + i \sinh\left( a\right) \sin\left( b\right) \end{eqnarray*}
© J. Carstensen (Math for MS)