Other complex functions

2.4 Other complex functions

Logarithm:
real values: $f(x)=e^x$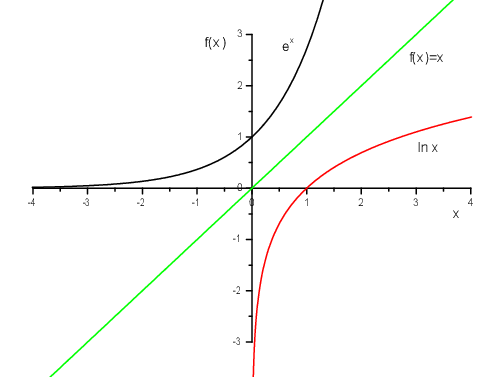

\begin{eqnarray*}w=e^x\rightarrow x&=&\ln w\qquad\Rightarrow f^{-1}(x)=\ln x \;\mbox{ is the inverse function with respect to $e^x$}\end{eqnarray*}

\[\ln 1 = 0 \qquad \ln e = 1 \qquad ln 0 = -\infty \]

now complex: \begin{eqnarray*}w=e^z&=&\left(e^a \cdot e^{ib}\right)\leftarrow\;2\pi \mbox{ periodic in b}\\ &\Leftrightarrow&z=\log w=\ln|w|+i\varphi+2\pi k i,\;k\in\mathbb{Z}\end{eqnarray*}

test:

\[e^z = e^{\ln|w|+i\varphi+2\pi k i} = e^{\ln|w|}\cdot e^{i\left(\varphi+2\pi k\right)}=|w|e^{i\varphi}=w\Rightarrow \mbox{o.k.}\]

Definition 9

\[f(z)= \log(z)=\ln|z|+i\varphi+2\pi k i,\;k\in \mathbb{Z}\; z=|z|e^{i\varphi}\]

$\qquad\qquad\qquad$is the complex logarithm of z. For $k = 0$ we get the main value.

Example: \begin{eqnarray*}\ln(-1)&=&\underbrace{\ln1}_{0}+i\underbrace{\varphi}_{\pi}+2\pi k i=i\pi+2\pi k i=i\pi(2k+1)\\ &\rightarrow&\mbox{logarithm of negative numbers now defined}\\& &\mbox{$\ln 0$ still $-\infty$}\end{eqnarray*}

Exponential function with arbitrary base:
real numbers: $\quad a^b=e^{b\ln a}\qquad a\gt0$
generalization for complex numbers: $\quad b\log a\qquad b\in \mathbb{C}, a\in\mathbb{C}\backslash\{0\} \Rightarrow a^b = e^{b\log a}=e^{b\left(\ln|a|+i\varphi_a+2\pi i k\right)}$

Definition 10 $0^0=1 $

special function: \begin{eqnarray*}f(z)&=&a^z,\quad a\gt0 \quad (a = e\mbox {-function})\\ f(z)&=&e^{z\log a}=e^{\ln a \;{\rm Re}(z)}e^{i\ln a \;{\rm Im}(z)}\quad\mbox{o.k.}\end{eqnarray*}

important (for root finding): \begin{eqnarray*}f(z)&=&z^b,\;\;b\in\mathbb{R}\qquad z=|z|e^{i\varphi}\\ \rightarrow f(z)&=&e^{b\log z}=e^{b\left(\ln|z|+i\varphi+2\pi i k\right)}\\ &=& e^{b\left(\ln|z|+i\varphi\right)}e^{2\pi i k b};\quad k\in\mathbb{Z}\\ \mbox{different cases: } b\in\mathbb{Z}&\rightarrow&e^{2\pi ik b}=1\rightarrow\;\mbox{o.k. "normal" power of z}\\ b \mbox{ irrational}&\rightarrow&e^{2\pi i k b}\;\mbox{infinite number of values}\\ b \mbox{ rational}&\rightarrow&e^{2\pi i k b}\; \hat{=} \;\mbox{finite number of values}\end{eqnarray*}

Example: \begin{eqnarray*}b&=&\frac{1}{n}\;:\;e^{2\pi i\frac{k}{n}}\; k=0,\ldots,n-1\\ \Rightarrow z^{\frac{1}{n}}&=&|z|^{\frac{1}{n}}e^{i\frac{\varphi}{n}}e^{2\pi i\frac{k}{n}}\quad k=0,\ldots,n-1\end{eqnarray*}

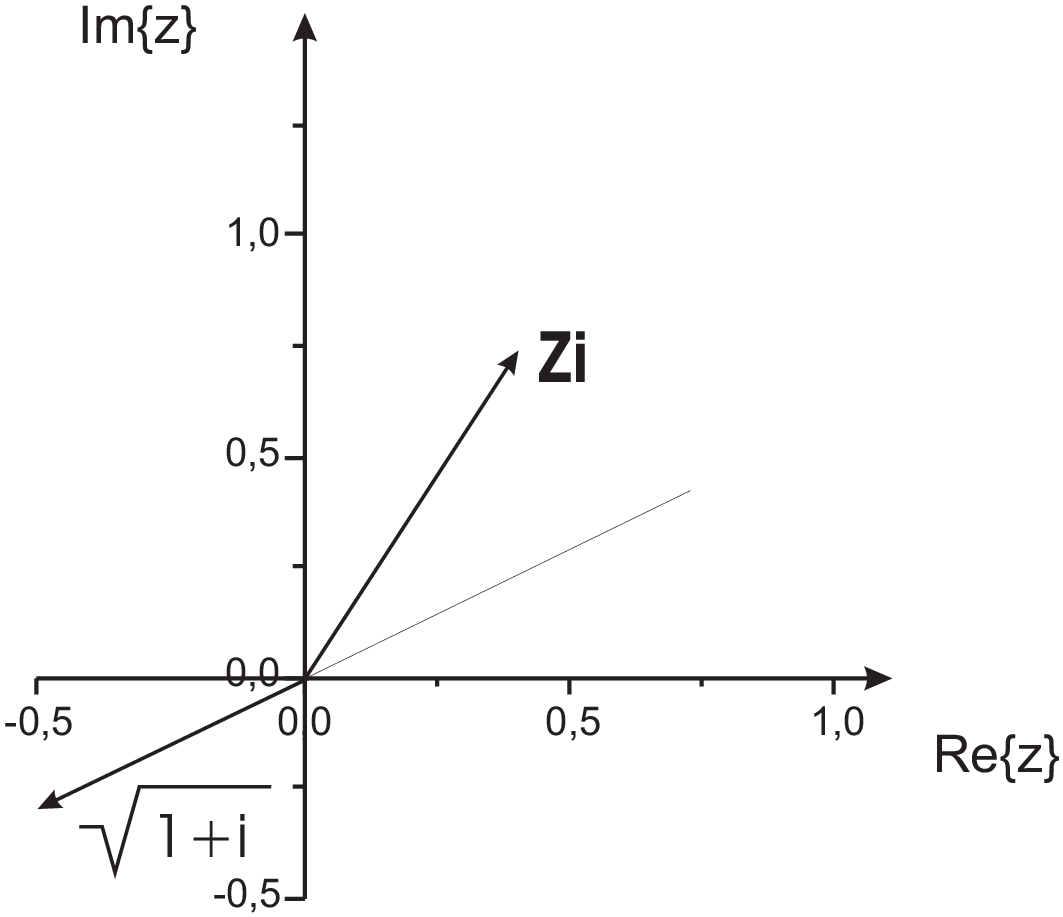
in particular: \begin{eqnarray*}n = 2\;:\;\sqrt{1+i}&=&\sqrt{2}^{\frac{1}{2}}e^{i\frac{\pi}{4}\frac{1}{2}}e^{2\pi i\frac{k}{n}}\;,k=0,1\\ \mbox{for $k=0$}&:&\sqrt{2}^{\frac{1}{2}}e^{i\frac{\pi}{8}}e^0=\sqrt{2}^{\frac{1}{2}}e^{i\frac{\pi}{8}}\\ \mbox{for $k=1$}&:&\sqrt{2}^{\frac{1}{2}}e^{i\frac{\pi}{8}}e^{\pi i}=\sqrt{2}^{\frac{1}{2}}e^{\pi i(1+\frac{1}{8})}=\sqrt{2}^{\frac{1}{2}}e^{\frac{9}{8}i\pi}\end{eqnarray*}

$\Rightarrow$ Roots are difficult functions, in particular not single values.
The most simple case we know already from square roots of pure positive real numbers $a$. The solution is

\[ \pm \sqrt{a} = e^{\frac{2 \pi i k}{2}} \sqrt{a} \]

which for $k \in \mathbb{Z}$ has the two independent solutions for $k = 0$ and $k = 1$.
Fundamental theorem of algebra
Each polynomial equation of degree $n\in\mathbb{N}$

\[a_nz^n+a_{n-1}z^{n-1}+\ldots+a_1z+a_0=0\]

with $a_0,\ldots,a_n\;\in\mathbb{C}$ has at least one solution $z\in\mathbb{C}$.
$\Rightarrow$ Say this is $z_1$, then:

\[\left(z-z_1\right)\cdot\left(b_{n-1}z^{n-1}+\ldots+b_0\right)=0\]

$\Rightarrow$ each polynomial has exactly $n$ solutions where so-called ”multiple zeros”, i.e. function $\left(z-z_0\right)^k$ count $k$-times.

\[\begin{array}{llcl} n=1&a_1z+a_0=0&\Rightarrow&z=-\frac{a_0}{a_1}\\ n=2&a_2z^2+a_1z+a_0=0&\Rightarrow&\mbox{quadratic equation}\\ n=3&a_3z^3+a_2z^2+a_1z+a_0=0&\Rightarrow&\mbox{solution via Cardano formula}\\ n=4&a_4z^4+\ldots+a_0=0&\Rightarrow&\mbox{solution via formula possible}\\ n\gt4& &\Rightarrow&\mbox{no formula exist for a general treatment!}\end{array}\]