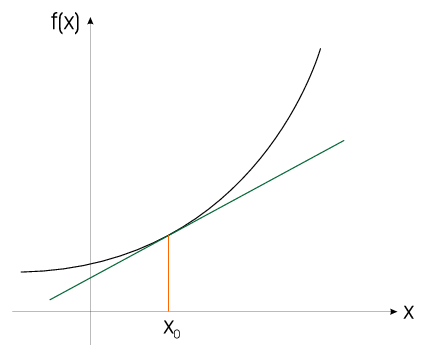3.5
Taylor series and their application
We have a ”normal” function \(f(x)\)
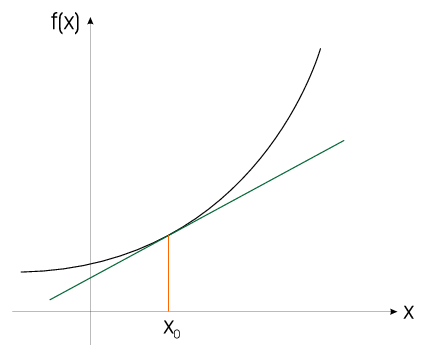
| \(f(x)\approx f(x_0)+(x-x_0)f'(x)\;\rightarrow\;\)
linear approximation!! |
Approximation of this function by a power series: \begin{eqnarray*}f(x)&=&f(x_0)+\frac{1}{1!}(x-x_0)f'(x_0)+\frac{1}{2!}(x-x_0)^2f''(x_0)+\ldots+\frac{1}{n!}(x-x_0)^nf^{n}(x_0)+\ldots\\
&=&\sum_{n=0}^\infty\frac{1}{n!}(x-x_0)^nf^{n}(x_0)\;\;\mbox{Taylor Series around the point $x_0$}\\ \Rightarrow f(x)&\approx&f(x_0)+(x-x_0)f'(x_0)+\mbox{O}((x-x_0)^2)\;\;\mbox{linear
approximation}\\ f(x)&\approx&f(x_0)+(x-x_0)f'(x_0)+\frac{1}{2}(x-x_0)^2f''(x_0)\;\;\mbox{quadratic approximation}\\ &\Rightarrow&\mbox{two
most important approximations in physics because:} \end{eqnarray*}
Potential:
|
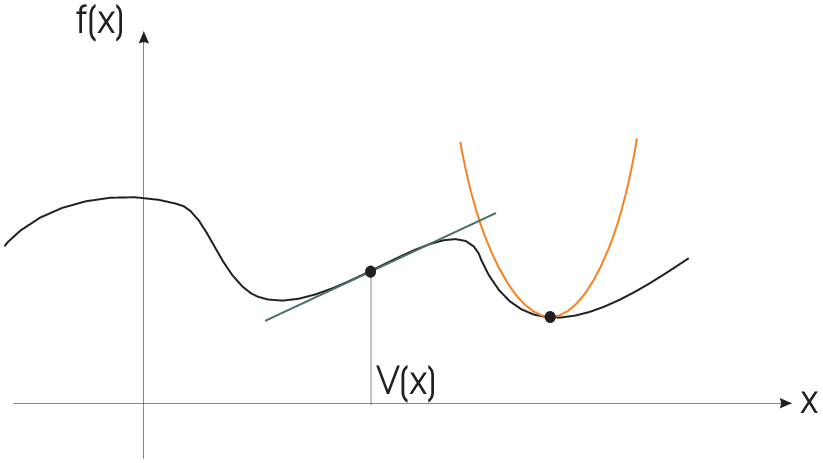
|
© J. Carstensen (Math for MS)