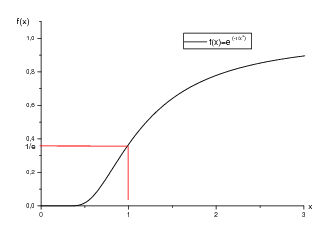
| \(f(x)^=e^{-\frac{1}{x^2}}\;\) if \(x\neq0\) and \(f(x)=0\) if \(x=0\). \(\rightarrow\) well defined function. |
If \(f(x)\) is a ”normal” function than \begin{eqnarray*} f(x)=f(x_0)&+&\frac{1}{1!}(x-x_0)f'(x_0)+\frac{1}{2!}(x-x_0)f''(x_0)+\ldots+\frac{(x-x_0)^{n-1}}{(n-1)!}f^{n-1}(x_0)\\ &+&\frac{(x-x_0)^n}{n!}f^n(x_0)+\frac{(x-x_0)^{n+1}}{(n+1)!}f^{n+1}(x_0+\epsilon\Delta x)\end{eqnarray*}
i.e. the error term
| \[\Delta f=\frac{(x-x_0)^{n+1}}{(n+1)!}f^{n+1}(x_0+\epsilon\Delta x)\quad\begin{array}{ccl}\Delta x&=&x-x_0\\0&\lt&\varepsilon\lt1\end{array}\] |
is the difference between the exact function and the approximation.
Example:
\begin{eqnarray*}f(x)&=&\sin x;\qquad x_0=0\\ \mbox{Taylor:}\;f(x)&=&x-\frac{x^3}{3!}+\frac{x^5}{5!}f^5(\epsilon
x)\qquad 0\lt\epsilon\lt1\\ f^5(x)&=&\cos x\Rightarrow\,\left|f(x)-\left(x-\frac{x^3}{3!}\right)\right|=|\Delta f|=\frac{x^5}{5!}|\cos(\epsilon
x)|\le\frac{x^5}{5!}\rightarrow\mbox{may diverge for large $x$}\\ \mbox{but for: } x&=&10^\circ=\underbrace{\frac{10\pi}{180}}_{0.17}\rightarrow\left|f(x)-(x-\frac{x^3}{3!})\right|\le10^{-6}
\end{eqnarray*}
Definition 32
| \[\sum_{k=0}^n\frac{f^k(x_0)}{k!}(x-x_0)^k\] |
is called a Taylor approximation or series of the order \(n\) to the function \(f(x)\) at the point \(x_0\).
Example: Approximation of third order to \(f(x)=e^x\) at \(x_0=0\):
| \[e^x\approx1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\mbox{O}(x^4)\] |
notation ”zero of \(x^4\)” means approximately up to \(x^3\)
exact
Sometimes problems: (rare cases)

| \(f(x)^=e^{-\frac{1}{x^2}}\;\) if \(x\neq0\) and \(f(x)=0\) if \(x=0\). \(\rightarrow\) well defined function. |
© J. Carstensen (Math for MS)