 |
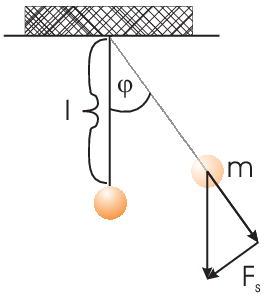
Motion of a pendulum:
 |
| \[s=l\varphi \qquad F_s=-mg\sin\varphi\] |
Newton: \begin{eqnarray*}F_s=m\ddot{s}&\rightarrow&\;m\ddot{s}=-mg\sin\varphi\\ l\ddot\varphi+g\sin\varphi=0&\rightarrow&\ddot\varphi+\omega^2\sin\varphi=0 \qquad(\star)\\ &&\qquad\varphi(t)=?\;\mbox{function is looked for ?}\\ \end{eqnarray*}
Eq. (\(\star\)) is extremely complicated since
it is non-linear because of the \(\sin\varphi\). For small \(\varphi\):
\(\sin\phi\approx\varphi\;\;\left|\sin\varphi-\varphi\right|\le\frac{\varphi^3}{3!}\approx10^{-3}\) for \(\varphi\le10^\circ\)
| \[\rightarrow\;\ddot{f}(t)+\omega^2f(t)=0\quad\frac{d^2\varphi}{dt^2}+\omega^2\varphi(t)=0\;\leftarrow\,\mbox{linear equation}\] |
See also exercises:
| \[f(t)=A_1e^{i\omega t}+A_2e^{-i\omega t}=\varphi\cos(\omega t)+\frac{\varphi}{\omega}\sin(\omega t)\] |
![]() Taylor series and error estimation
Taylor series and error estimation
© J. Carstensen (Math for MS)