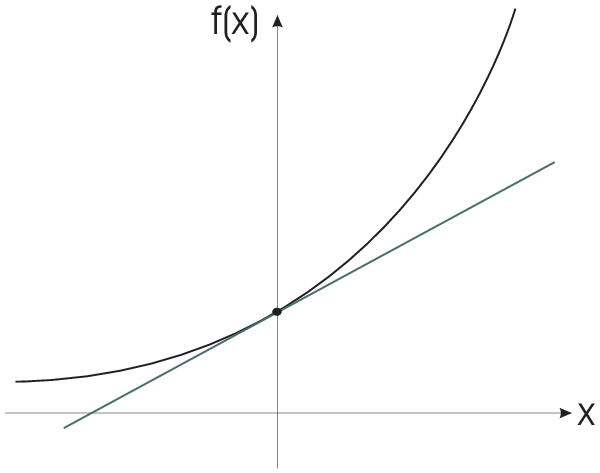
| \begin{eqnarray*}f(x)&=&e^x,\qquad x_0=0\\ f(x)&\approx&e^0+\frac{1}{1!}(x-0)f'(0)=1+x\\ x_0&=&1\qquad f(x)\approx e^1+(x-1)e^1=ex\\ x_0&=&-1\qquad f(x)\approx e^{-1}+(x-(-1))e^{-1}=\frac{1}{e}x+\frac{2}{e}\\ &\rightarrow&f(x)=\sum_{n=0}^\infty\frac{1}{n!}x^n\end{eqnarray*} |
With frame
Taylor series and their application