Example: Taylor expansion of cos function

3.5.3 Example: Taylor expansion of cos function

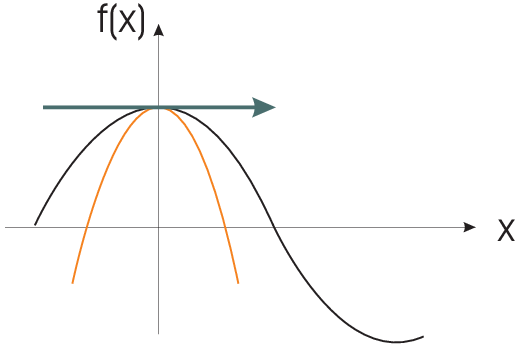
\begin{eqnarray*} f(x)&=&\cos x;\qquad x_0=0\\ f(x)&\approx&\cos0+x(-\sin0)\approx1\\ f(x)&\approx&1-\frac{1}{2}x^2\\ f'(x)&=&-\sin x\rightarrow f''(x)=-\cos x\rightarrow f'''(x)=\sin x\\ & & \qquad \quad \rightarrow f''''(x)=\cos x=f(x)\\ \Rightarrow f(x)&=&\sum_{n=0}^\infty\frac{(-1)^b}{(2n)!}x^{2n}=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\ldots\end{eqnarray*}

\begin{eqnarray*} f(x)&=&e^{ix}\\ &=&\sum_{n=0}^\infty\frac{(ix)^n}{n!}=\sum_{n=0}^\infty\frac{i^nx^n}{n!}=1+ix-\frac{1}{2!}x^2-\frac{i}{3!}x^3+\frac{1}{4!}x^4+\ldots\\ &=&\left(1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\ldots\right)+i\left(x-\frac{x^3}{3!}+\ldots\right)=\cos x+i\sin x\end{eqnarray*}

With frame

Taylor series and their application