 |
2. Zeige, daß y1(x)
= A · exp (ikx) + B · exp –(ikx) eine Lösung der Schrödinger-Gleichung
in Gebiet (1) ist. |
|
 |
A und B sind von 0 verschiedene Konstanten, und i
ist die imaginäre Einheit; i2 = –1. |
 |
Zweifaches Ableiten dieser Wellenfunktion liefert:
|
| |
| y1(x) | = |
A · exp(ikx) | + |
B · exp(–ikx) | | | |
| | |
¶2y1(x)
¶x2 | = |
– k2 · A · exp(ikx) | –
| k2 · B · exp(–ikx) |
| | | | |
| | | = |
– k2 · y1(x) |
| |
|
|
|
 |
Dieses Ergebnis wird in die Schrödinger-Gleichung eingesetzt. Wir erhalten dann das folgende
Resultat:
|
| |
| – k2 · y1(x) |
+ | 2m
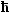 2 2 |
· E · y1(x) |
= 0 | | | |
| | |
| – k2 | + |
2m
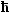 2 2 | · E | = 0 |
|
|
|
 |
Das ist eine Bedingung für die Größe k: Der gemachte Ansatz
ist also nur dann eine Lösung falls gilt: |
| |
| k | = |
± |
æ
ç
è |
2m
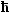 2 2 | · E |
ö
÷
ø |
1/2 | = |
(2m · E)½
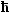 | = |
(m2 · v2)½
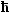 | | | |
| |
| |
| |
| |
| |
| k | = |
p
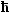 | := | 2 p
l | |
| |
| |
| |
|
|
|
 |
Dabei haben wir von folgenden Beziehungen Gebrauch gemacht:
- Die Gesamtenergie muß ausschließlich kinetisch sein - das Potential
ist ja = 0 - also gilt E = ½mv2.
- Der durch Einsetzen erhaltene Ausdruck m2v2 ist natürlich das Quadrat des Impulses
p.
- Die de Broglie Beziehung sagt uns, daß p/
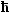 = 2p/l, das ergibt die letzte Gleichung. = 2p/l, das ergibt die letzte Gleichung. |
|
 |
Damit können wir die Zusatzfrage angehen: |
| | |
 |
Was wird durch k physikalisch beschrieben? Hinweis: Beachte die Dimension und die allgemeine Form der
Lösung (verwende den Eulerschen Satz). |
 |
y1(x) löst die Schrödingergleichung
für geignet gewählte Parameter. Schreibt man die komplexen Exponentialfunktionen mit Hilfe der Eulerschen Beziehung
aus, ergibt sich eine Folge von sin und cos Funktionen mit dem Argument k · x. |
|
 |
Wie auch immer es genau aussieht, das ist etwas wellenartiges, und k ist bis
auf das 2p so etwas wie die Wellenzahl 1/l, weiter bis
bis auf das 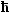 der Impuls p = mv - und sogar die Energie E steckt codiert in k. der Impuls p = mv - und sogar die Energie E steckt codiert in k.
|
|
 |
Es ist schlicht die beherrschende Größe, in der alle Eigenschaften
des Teilchens stecken! |
|
 |
In drei Dimensionen ist k ein Vektor, man
nennt es den Wellenvektor des Teilchens; mit ihm haben wir einen zentralen Begriff der
Quantentheorie kennengelernt. |
| |
 |
5. Berechne die Aufenthaltswahrscheinlichkeit |y2(x)|2 des Teilchens in Gebiet (2) und vergleiche das Ergebnis
mit der Erwartung für ein klassisches (nicht quantenmechanisches) Teilchen. |
 |
Die Aufenthaltswahrscheinlichkeits(dichte) eines Teilchens am Ort x
wird durch das Betragsquadrat der Wellenfunktion an dieser Stelle gegeben.
Für Gebiet (2) lautet sie hier:
|
|
|
| |y2(x)|2 |
= |
C2 · exp(–2ax) |
= C2 · exp[–2x · {(2m/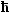 2) · (V0
– E) ·}½] 2) · (V0
– E) ·}½] |
|
|
|
 |
Da V0 > E vorausgesetzt wird, ist a
reell und wir haben schlicht eine abklingende Exponentialfunktion. |
| |
|
 |
Was würden wir für ein klassisches
Teilchen erwarten? Zum Beispiel für eine Kanonenkugel, die auf einen Tafelberg zufliegt, mit einer Flughöhe die
kleiner ist als die Berghöhe? |
 |
Für klassische Teichen erwarten wir einfach perfekte Reflektion: Niemals, auch nicht einmal ansatzweise, ist das Teilchen im Bereich (2) zu finden. |
|
 |
Unser quantenmechanische Teilchen kann jedoch mit einer endlichen Wahrscheinlichkeit nach
Maßgabe der obigen Formel im Bereich (2) gefunden werden! Es kann in Bereiche eindringen, die klassischen Teilchen
vollständig verwehrt sind. |
|
 |
Die folgende Graphik zeigt schematisch wie das aussieht (für C = 1) |
| |
|
|
 |
Die Graphik zeigt auch wie diese Lösung im Bereich (1) aussehen würde, wo
sie aber keinen Sinn ergibt (siehe unten)! |
 |
8. Welcher Grenzfall führt bei diesem Problem auf
das klassische Ergebnis? |
 |
Obwohl es klassische Teilchen gar nicht gibt, wird der Tunneleffekt
bei "normalen" Verhältnissen nie beobachtet. Es ist jetzt auch leicht
zu sehen warum: |
|
 |
Um das klassische Ergebnis zu erhalten, muß die Aufenthaltswahrscheinlichkeit |y2(x)|2
Þ 0 gehen. Dies können wir auf zwei Weisen erreichen:
|
|
 |
1. Indem wir a Þ
¥ laufen lassen. Dies entspricht einer unendlich hohen
(nicht überwindbaren) Potentialstufe. Die Wahrscheinlichkeit, das Teilchen in Gebiet (2) anzutreffen, ist dann
immer gleich null, so daß wir auf das klassische Ergebnis kommen. |
 |
Das ist aber nicht sehr befriedigend; wir wollen ja nicht nur bei großen
Energiedifferenzen zur klassischen Betrachtung kommen. Besser ist: |
|
 |
2. Die Teilchenmasse wird erhöht. Nehmen wir ein Proton, anstelle eines Elektrons, d.h. rund und roh die 2
000 fache Masse, wird |y2(x)|2 mit exp–( 2 000)1/2
= 3,78 · 10–20 multipliziert - spätestens jetzt ist die Wahrscheinlichkeit ziemlich dicht
bei Null! |
| |
|
© H. Föll (MaWi 1 Skript)
![]() Working with Exponentials and Logarithms
Working with Exponentials and Logarithms