 |
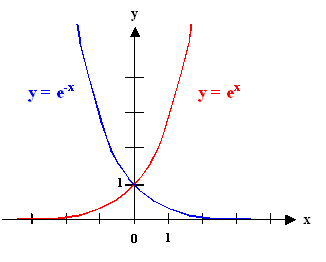
First, the graphical representation of the most important exponential curves (see math script as well) |
| |
| |
|
|
 |
The typical curves everybody should know. The blue curve in the first quadrant (positive x
values) corresponds to the energy dependence of the ubiquitous Boltzmann
factor exp – (E/kT) |
 |
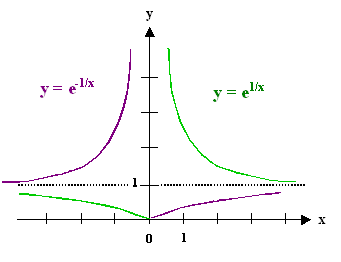
Slightly more tricky. Note that the purple branch in the 1. quadrant corresponds to
the temperature dependence of the ubiquitous Boltzmann factor exp – (E
/kT) |
 |
The inverted functions, e.g. y = ln x are easily pictured, too; below the
y = ln x and the y = ln (1/x) functions are shown. |
|
|
|
 |
The graphs, in case you forgot, also illustrate some basic algebraic relations, e.g.
- e– x = 1/ex
- ln x = – ln (1/x)
|
 |
The essential identities are |
| |
| ex | = |
1
e– x | |
(ex)y | = |
ex · y | |
| | | |
| |
| |
| ex · ey |
= | ex + y |
| (ex)1/y |
= | ex /y |
|
| | |
| |
| |
|
| ex
ey | = |
ex – y | |
eln x | = |
x |
|
| |
| ln (x · y) | = |
ln x + ln y |
| | |
| | ln |
x
y | = |
ln x – ln y |
| | |
|
| ln xy | = |
y · ln x |
|
|
 |
Here some approximations. |
| |
| ex | = |
1 + | x
1! |
+ | x2
2! |
+ | x3
3! |
+ .. |
|
| |
| ln (1 + x) | = |
x – | x2
2 |
+ | x3
3 |
– | x4
4 |
+ .. | |
| ln (1 – x) | = |
– | æ
è
| x + | x2
2 |
+ | x3
3 |
+ | x4
4 |
+ .. | ö
ø
|
|
|
 |
While many equations contain exponential terms of some variable
which "disappear" if you substitute the ln of the variable (as in the Arrhenius
plot), we mostly prefer the lg of some observable quantity to the ln. As an example, plotting the
vacancy concentration
cV in an Arrhenius plot would be straight forward with the ln: |
|
 |
On order to get a straight slope we have to switch to new variables according
to |
| |
| ln cV | = ln A – |
HF
kT | · | 1
T |
for
|
|
|
 |
For y and x we get straight line with slope –HF/k
and intercept = A |
 |
What do we have to do if we want to plot lg (cV)
instead of ln (cV)? |
|
 |
We have to multiply everything with lg e = 0,4342.., because |
| |
| lg x | = | (lg e) · (ln x) |
1) |
|
|
|
 |
We obtain |
|
|
| lg (cV) | = |
0,434 · ln A – 0,434 · |
HV
k | · |
1
T |
|
|
| |
|
© H. Föll (MaWi 1 Skript)
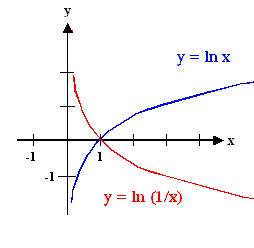
![]() 5.3.3 Gleichgewichtskonzentration von atomaren Fehlstellen in Kristallen
5.3.3 Gleichgewichtskonzentration von atomaren Fehlstellen in Kristallen ![]() 5.3.2 Definition der Entropie und erste Anwendung
5.3.2 Definition der Entropie und erste Anwendung ![]() 5.3.4 Darstellungen der Konzentrationsfunktion
5.3.4 Darstellungen der Konzentrationsfunktion