Schrödingergleichung und Wasserstoffatom

	Im folgenden wird in Kurzform der Weg zur Lösung der Schrödingergleichung für das Wasserstoffatom skizziert. Dies ist, es sei nochmal darauf hingewiesen, ein rein mathematisches Problem.
		Einige Vertrautheit mit partiellen Differentialgleichungen wird vorausgesetzt.
	Die Schrödingergleichung für das Wasserstoffatom lautet
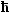		– 2 2m æ ç è ¶2y(x,y,z) ¶x2 + ¶2y(x,y,z) ¶y2 + ¶2y(x,y,z) ¶z2 ö ÷ ø + æ ç è e2 4pe0r –  E ö ÷ ø · y(x,y,z) = 0
		mit r = (x2 + y2 + z2)1/2
	Da es sich um ein radialsymmetrisches Problem handelt, macht man (als Mathematiker) jetzt automatisch eine Transformation von cartesischen (x,y,z) Koordinaten zu Kugelkoordinaten (r, d, j). Dies ist recht aufwendig, aber altbekannt. Um Verwechslungen des Winkels d mit dem hier benutzten Zeichen für die partielle Differentiation auszuschließen, benutzen wir jezt das "d" als Symbol auch für partielle Ableitungen. Wir erhalten:
d2y dr2 + 2 r · dy dr + 1 r2 æ ç è 2 sind · d dd æ è sind  ·  dy dd ö ø + 1 sin2d · d2y dj2 ö ÷ ø + 8mep2 h2 æ è E + e2 4pe0r ö ø y = 0

		Sieht nicht gerade einfach aus. Aber nicht verzweifeln, der Mathematiker kennt so was und weiß, daß der nächste Schritt ein Separationsansatz ist: Wir probieren mal, ob eine Darstellung der gesuchten Lösung als Produkt aus drei Einzelfunktionen, die jede nur von einer der Variablen abhängt, weiterführt. Wir schreiben also versuchsweise
		y(r,d,j)  =  R(r) · Q(d) · F(j)
	Nach scharfem Nachdenken folgt ziemlich schnell als erstes Ergebnis
		F(j)  =  exp ± (i · m · j) für jedes ganzzahlige m
	Damit läßt sich die S.-Gleichung verkürzen auf die noch zu bestimmenden Funktionen R(r) · Q(d), wir erhalten
r2 R æ ç è d2R dr2 + 2 r · dR dr + 8mep2 h2 æ è E + e2 4pe0r ö ø ö ÷ ø · R  =  –  1 Q · æ ç è 1 sind · d dd æ è sind dQ dd ö ø  –   m2Q sin2d ö ÷ ø

	Die Gleichheit zweier beliebiger Funktionen die von verschiedenen Variablen abhängen, wie sie die obige Gleichung verlangt, kann nur gegeben sein, wenn der linke und der rechte Term für beliebige Werte von r oder d immer eine Konstante, wir nennen sie mal a, ergibt.
		Damit haben wir jetzt zwei Differentialgleichungen, eine für R und eine für Q. Schauen wir zunächst die für Q näher an. Wir haben (gleich etwas umgeschrieben)
		1 sind · d dd æ è sind dQ dd ö ø  +   æ è a  –  m2 sin2d ö ÷ ø Q  =  0
		Der Mathematiker freut sich, denn diese Geichung kennt er: Es ist die Definitionsgleichung für die Kugelflächenfunktionen, altbekannt (wenn auch nicht leicht zu lösen) von vielen klassischen Problemen.
	Zunächst zeigt sich, daß diese Gleichung nur Lösungen hat falls a = (k + m) · (k + m + l) gilt, wobei k und m eine positive ganze Zahl sein muß. Wir benutzen hier gleich das Symbol "m", weil es sich herausstellen wird, daß es identisch sein muß zu dem bereits eingeführten m.
		Für k + m benutzen wir ein neues Symbol, nämlich l, und nennen die zu a = l · (l + 1) gehörende Lösung "Kugelwellenfunktion l-ter Ordnung".
		Davon gibt es l + 1 verschiedene, da m den Wertebereich von 0 bis l durchlaufen kann (genau hinschauen).
	Man kann jetzt die Mannigfaltigkeit der Lösungen durchgehen. Sie sind alle bekannt und jeder hat sie schon gesehen:
		Dabei ist der Wert für l entscheidend für die Komplexität: Für l = 1 gibt es eine Kugel; für l = 2 die Kugeldoppelkeule, etc. Der Wert für m gibt die verschiedenen Orientierungen im Raum oder sonstige Varianten wieder.
	Wenden wir uns der Differentialgleichung für R zu. Statt mit a können wir die Gleichung jetzt mit l · (l + 1) formulieren und erhalten
		d2R dr2 + 2 r dR dr  +  æ ç è 8mep2·E h2  +  8mep2e2 4h2pe0r  –   l · (l + 1) r2 ö ÷ ø · R  =  0
		Jetzt wird es trickreich. Auch der Mathematiker braucht uns wieder: Von allem möglichen Lösungen, die diese Differentialgleichung noch zuläßt, müssen einige auf Grund physikalischer Kriterien ausgeschieden werden, d. h wir müssen Randbedingungen definieren, z.B. daß y(r ® ¥) = 0 sein muß - sehr weit weg vom Atomkern wollen wir keine Elektronen mehr finden!
	Nach längerer Rechnung findet man zwei wichtige allgemeine Aussagen
	1. Alle Lösungen kann man wie folgt darstellen:
		R  = v(r) · exp –   æ ç è r · æ ç è – 8mep2·E h2 ö ÷ ø 1/2 ö ÷ ø
		with v(r) being some function that must now be determined from a somewhat simpler differential equation resulting after plucking this formula into the differential equation for R(r).
		Note that the argument of the exponential in the equation for R contains the root of something negative: (–8mep2·E/h2)1/2 - this is the point where the solutions of the S.- equations become complex!
		(Entschuldigung; ist so reingerutscht - aber Englisch muß für einen Materialwissenschaftler selbstverständlich sein).
	2. Lösungen existieren nur falls immer gilt
		æ ç è 8mep2·e2 4pe0h2 ö ÷ ø 2 = n2 · 8mep2·E h2
		wobei n = 1,2,3,4... sein muß.
		Damit haben wir eine Formel für die Energie gefunden, die uns bekannt vorkommt: .
		En = – 1 n2 me4 8e02 h2
	Wenn man die Lösungen jetzt schließlich ausrechnet (mit erheblicher Mühe), findet man, daß der Radialteil der Wellenfunktion, also R(r), von r = 0 ausgehend immer schnell auf 0 abklingt, wobei er je nach n, noch ein paar Male (n - 1 mal, um genau zu sein) zwischen positiven und negativen Werten hin und her oszilliert - so haben wir das auch schon gemalt.
	Nun setzen wir alles zusammen, bilden also das Produkt
		y(r,d,j)  =  R(r) · Q(d) · F(j)
	Damit bekommen wir:
		1. genau die Orbitale, die wir als Lösungen einfach postuliert haben, 2. Die diversen Beziehungen zwischen den drei Quantenzahlen n, l, m, die aus der Lösung "herausgefallen" sind, 3. Eine simple Gleichung für die Gesamtenergie E, die beim Wasserstoffatom nur von der Hauptquantezahl n abhängt, und 4. ein Gefühl dafür, was auf uns zukäme, wenn wir jetzt zum He Atom schreiten würden, oder noch ein Magnetfeld einschalten, oder sonst noch ein bißchen zusätzliche Komplexität einführen.
	Wow!!! Es könnte jetzt der Eindruck entstanden sein , das sei schwierig.
		Ist es aber nicht - es ist nur kompliziert. Wir haben halt keine einfache Methode, relativ einfache dreidimensionale Körper durch mathematische Gleichungen darzustellen.
		Sind die oben gezeigten Kugelwellenfunktionen schwer vorstellbar?
	Eben! Nur die Formeln drumrum sind länglich. Da wir weder Mathematiker noch Physiker sind, lassen wir uns von dem mathematischen Gerüst nicht schrecken - meistens reicht das Vorstellungsvermögen für das was die Gleichungen beschreiben für unsere Zwecke völlig aus.

Mit Frame

2.1.3 Schroedingergleichung und Wasserstoffatom

2.1.4 Loesung der Schroedingergleichung fuer das Wasserstoff Atom

© H. Föll (MaWi 1 Skript)