 |
Bevor wir das thermodynamische
Gleichgewicht näher behandeln, müssen wir einige Grundelemente der Thermodynamik
näher betrachten oder uns ins Gedächtnis zurückrufen. Wir wollen dazu nicht, wie üblich und durchaus
nützlich, die historische Entwicklung nachvollziehen, sondern gleich die wichtigsten Aussagen der "modernen"
statistischen
Betrachtung der Thermodynamik verwenden - auf immer verbunden mit dem Namen Ludwig Boltzmann (siehe auch Thermodynamik
Skript). |
|
 |
Dem einen oder der anderen mag es bei dem Begriff "statistische"
Thermodynamik grausen. Dieser Teil der Physik gilt als schwer und mit länglichen Formeln und merkwürdigen Begriffen
wie "großkanonische Gesamtheit" oder "Ergodenhypothese
" befrachtet. |
|
 |
Das ist schon richtig - aber nicht für uns bei dieser Vorlesung. Hier gilt das genaue
Gegenteil: Die Grundlagen der statistischen Thermodynamik sind (bei Verzicht auf einige trickreiche Herleitungen wesentlicher
Formeln) viel einfacher zu verstehen, als die Grundlagen der klassischen Thermodynamik! |
 |
Zunächst brauchen wir den ersten
und zweiten Haupsatz der Thermodynamik. |
 |
Der erste Hauptsatz ist
im Grund nichts anderes als der altbekannte Energieerhaltungssatz, aber ergänzt
durch die monumentale Entdeckung Robert
Mayers, daß Wärme eine Energieform ist. |
|
 |
Über das "mechanische Äquivalent":
1 cal = 4,18 J läßt
sich Arbeit (gemessen in Joule, J)
in Wärme (gemessen in Kalorien, cal) umrechnen und umgekehrt. |
 |
Zum zweiten Haupsatz
kommt man, wenn man berücksichtigt, daß zwar mechanische Arbeit oder Energie sich immer zu 100 % in Wärme
umsetzen läßt, Wärmeenergie aber nie zu 100 % in mechanische Arbeit.
|
|
 |
Der zweite Hauptsatz berücksichtigt damit, daß viele Prozesse im Universum irreversibel sind; sie können nicht umgekehrt werden. |
|
 |
Hier steckt ein tiefes Rätsel der Natur: Rückwärtslaufende Filme der menschliche
Welt sind sofort als mit der Erfahrung unvereinbar zu erkennen, während in der Zeit rückwärtslaufende "Filme"
aller Vorgänge auf der Ebene der Elementarteilchen nicht von den in der Zeit vorwärtslaufenden zu unterscheiden
sind. |
|
 |
Woher kommt diese offenbar vorgegebene Richtung
der Zeit von der Vergangenheit
in die Zukunft in makroskopischen
Dimensionen? Denn in mikroskopischen Dimensionen gibt es keine
Richtung der Zeit! In allen Formeln kann t durch –t ersetzt werden, ohne daß etwas
falsch wird. |
|
 |
Der 2. Haupsatz postuliert als einziges physikalische
Grundgesetz eine Richtung der Zeit. Er hat damit etwas Geheimnisvolles, denn eine Richtung der Zeit ist aus den anderen
pysikalischen Grundgesetzen nicht zu erkennen. Der 2. Haupsatz war und ist einer der zentralen Sätze mit dem
sich philosophierende Naturwissenschaftler beschäftigen. Mehr dazu
im Link. |
 |
Die Thermodynamik mit all ihren Verästelungen, Wärmekraftmaschinen und
Perpetuum Mobiles war lange Zeit eine phänomenologische
Theorie - und zwar eine sehr erfolgreiche. |
|
 |
Wärme war eine Form von Energie, soviel war klar, aber was genau
einen warmen von einem kalten Körper im Inneren unterscheidet, war nicht klar (die Atome waren noch nicht "erfunden"). Im übrigen beschäftigt sich die klassische
Thermodynamik vorzugsweise mit Gasen, die uns in der Materialwissenschaft weniger interessieren. |
|
 |
Wir ersparen uns hier weitgehend die phänomenologischen Grundlagen und konzentrieren
uns auf einige wenige Schlüsselaussagen der statistischen Theorie der Wärme,
in der alle Begriffe der phänomenologischen klassischen Thermodynamik auf das Verhalten der Atome zurückgeführt
sind. |
 |
Trotzdem sollte der Materialwissenschaftler die Grundzüge der klassischen
Theorie kennen. Dazu kann man bei dem entsprechenden Basisbegriff
nachschauen (im Hyperscript "Defects"),
oder Bücher zur Thermodynamik zu Rate ziehen. |
| |
|
|
Der 1. Hauptsatz der Thermodynamik |
| |
|
 |
Doch nun zum ersten Hauptsatz der TD (so kürzen wir Thermodynamik gelegentlich ab).
|
|
 |
Wir betrachten ihn, abweichend vom normalem Vorgehen, zunächst in einer
mehr modernen Form. Wir wissen nämlich schon, daß Wärme eine Form von
Energie darstellt, daß es Atome gibt und daß
Energie immer als kinetische und/oder potentielle
Energie der Atome oder Moleküle (in den entsprechenden elektrischen-, magnetischen- oder Gravitationsfelder) aufgefaßt
werden kann. |
|
 |
Als Ausgangspunkt betrachten wir die innere Energie eines
Teilchensystems. "Innere" heißt, daß wir nur die dem System innewohnenden
wichtigen Energiebeiträge mitnehmen, die zum Teil schon durch die Wahl eines "inneren" Koordinatensystems bestimmt sind.
|
|
 |
Wenn wir z.B. einen Si-Kristall betrachten, der auf einem Tisch liegt und den wir vielleicht
heiß oder kalt machen und evtl. noch irgendwelchen Drücken aussetzen wollen, interessiert uns nicht die kinetische
Energie, die im Kristall steckt weil sich die Erde um die Sonne bewegt usw.; diese Beiträge sind auch automatisch weg
wenn wir unser Koordinatensystem am Kristall (oder, in dem Beispiel, am Tisch) "festmachen". In diesem Beispiel
interessiert uns aber auch nicht unbedingt die potentielle Energie des Si-Kristalls im Schwerefeld der Erde, weil
sie im Vergleich zur kinetischen und elektrostatischen Energie der Atome klein ist und sich vor allem bei unseren geplanten
Manipulationen nicht ändert. |
|
 |
Uns interessieren nur Energiebeiträge, auf die wir
Einfluß nehmen können, die sich ändern können; z.B. indem man dem
System Wärmeenergie zuführt. Damit fallen (fast immer) auch die Energien der inneren Elektronen weg; denn die
können wir nur beeinflussen, wenn wir (per Kernspaltung) die Atome ändern. |
|
 |
Da bei einem Stück Si das nur so rumliegt auch keine chemischen Reaktionen stattfinden
(im wörtlichen oder im erweiterten Sinn), können wir die Energien der Elektronen auch weitgehend ignorieren.
|
 |
Was für unseren Si-Kristall
(oder jeden anderen festen Körper) bleibt, ist also nur noch die ungeordnete kinetische Energie der um ihre Gleichgewichtslage
im Gitter schwingenden Atome, zusammen mit der aus dem Bindungspotential kommenden potentiellen Energie.
|
|
 |
Wenn wir ein Gas betrachten, ist es die nur
die kinetische Energie der im vorgegebenen Volumen ungeordnet
(="statistisch") herumsausenden Atome und Moleküle. Bei Molekülen muß man evtl auch noch
die Energie mitbetrachten, die in Rotationen und Schwingungen steckt. |
 |
Betrachten wir, was geschieht, wenn man einem solchen System Energie in Form von
Wärme zuführt. Wir wollen dies im direkten Vergleich Festkörper (= Kristall) und Gas tun:
|
|
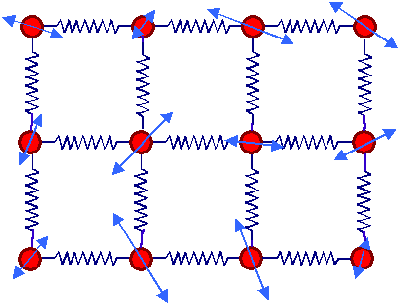
| Festkörper |
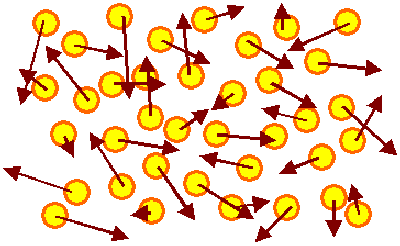
Gas |
 |
 |
| Die Atome schwingen in ihrem Potentialtopf
(symbolisiert durch Federn) um die Gleichgewichtslage (angedeutet durch blaue Doppelpfeile). Dies ist eine Momentaufnahme
mit Bezug auf die Geschwindigkeiten mit ganz kurzer Belichtungszeit. Wenige Picosekunden später sehen die Doppelpfeile
überall anders aus; die in der Bewegung steckende innere Energie (= Summe aus der
mittleren kinetischen und potentiellen Energie der Schwingungen) bleibt aber konstant. |
Die Atome (oder auch Moleküle) fliegen mit konst. Geschwindigkeit (angedeutet
durch braune Pfeile) durch den verfügbaren Raum. Dies ist eine Momentaufnahme mit
ganz kurzer Belichtungszeit. Wenige Nanosekunden später sehen die Pfeile überall anders aus, da sich durch Stöße
die Vektoren ständig ändern. Die in der Bewegung steckende innere Energie (= Summe der kinetischen Energie
der Teilchen) bleibt aber konstant. |
| Wir führen jetzt Wärme zu (d.h. wir erhöhen
die Temperatur) |
| Damit erhöht sich die innere
Energie durch: |
| Erhöhung der mittleren kinetischen Energie der Schwingung und
Erhöhung der mittleren potentiellen Energie durch Abweichungen von der Ruhelage im Potentialtopf
des Atoms in seiner Bindungsumgebung |
Ausschließliche Erhöhung der kinetischen Energie der Gasteilchen (mit
möglichen Energieanteilen in Translation, Rotation und Schwingungen). |
| Da die potentielle Energie und die Schwingungsenergie im Prinzip unabhängig voneinander
sind (man könnte gedanklich einem Atom nur potentielle Energie zuführen, d.h. den Abstand zum Nachbarn ändern
ohne die momentane Geschwindigkeit zu ändern und umgekehrt), hat ein Atom im Kristall 6
Freiheitsgrade um Energie aufzunehmen: 3 für potentielle Energie und 3
für kinetische Energie - je ein Freiheitsgrad pro Raumrichtung. |
Ein 1-atomiges Gas hat 3
Freiheitsgrade, es kann Energie nur durch Bewegung in jede der drei Raumrichtungen aufnehmen.
Bei einem 2-atomigen Gas wird es komplizierter: Zu den 3 Freiheitsgraden der Translation
kommen im Prinzip noch 2 Freiheitsgrade der Rotation (es kann um zwei Achsen senkrecht zur Bindungsrichtung rotieren) und Freiheitsgrade möglicher
Schwingungen . |
|
 |
Wir
haben schon mehrfach den einfachen Zusammenhang benutzt, daß die Temperatur ein Maß für die dem System
innewohnende innere Energie ist. Der quantitative Zusammenhang ist durch eine einfache
Proportionalität gegeben, die Proportionalitätskonstante ist die Boltzmannkonstante
k. |
|
 |
Wir müssen aber beachten, daß es je nach System unterschiedlich viele
Möglichkeiten dafür gibt, Energie aufzunehmen; die Zahl der unabhängigen Möglichkeiten heißen
die Freiheitsgrade
f des Systems.
|
|
 |
Ein zweiatomiges Molekül könnte beispielsweise Energie aufnehmen, indem es seine
Geschwindigkeit in eine der drei Raumrichtungen erhöht, schneller um eine Achse rotiert, oder mit größerer
Amplitude schwingt. Jede Möglichkeit ist ein Freiheitsgrad. Wieviele es jeweils gibt, mag schwer zu beurteilen sein,
jedenfalls sind es aber immer nur endlich viele. |
|
 |
Aus der statistischen Thermodynamik
ergibt sich ein einfacher Zusammenhang zwischen der Temperatur T und der Energie E (wer will,
darf das auch als Definition der Temperatur betrachten). |
|
 |
Dieser Zusammenhang heißt Gleichverteilungsatz;
er ist so elementar einfach und gleichzeitig so ungeheuer wichtig, dass die Formel herausgehoben werden soll: |
| |
|
|
 |
Das bedeutet in Worten, daß pro Freiheitsgrad und Teilchen im Mittel 1/2 · kT
thermische Energie im System steckt. Ein Ansatz zu einer Herleitung findet sich im Link. |
 |
Die Energie E ist dabei die innere Energie
wie oben definiert; zukünftig wollen wir sie als spezielle Energie mit einer anderen
Abkürzung versehen nämlich mit dem Buchstaben U. |
|
 |
Dazu nachen wir jetzt eine Übung |
| |
|
 |
Diese simple Beziehung ist zwar (noch) nicht der erste Haupsatz, enthält aber seinen Kernpunkt,
nämlich den Verbleib der in einen Körper hineingesteckten Wärmeenergie. |
|  |
Die Formel kann (mit einigem Aufwand) zwar ganz sauber aus der statistischen Mechanik hergeleitet werden,
hat aber große Probleme aufgeworfen, denn sie ist gelegentlichen ganz eindeutig falsch,
wenn man sie experimentell überprüft. Reale Systeme scheinen manchmal weniger
Freiheitsgrade zu haben, als definitiv da sein müssen. In dieser Beobachtung steckte einer der Stolpersteine
der Physik zu Beginn des 20. Jahrhunderts, der erst (von Albert
Einstein) mit der Quantentheorie überwunden wurde. |
|
 |
Das Problem war, daß nicht alle vorhandenen Freiheitsgrade eines Systems beobachtet wurden. Zum Beispiel
kann in einem 2-atomigen Molekül Energie auch in einer Schwingung der Atome gegeneinander aufgenommen werden;
diese Schwingung ist ein gültiger Freiheitsgrad des Systems. Klassisch kann diese
Schwingung mit beliebig kleiner Amplitude stattfinden, und damit auch beliebig kleine Energiebeiträge aufnehmen - sie
sollte immer beobachtbar sein. |
|
 |
Quantenmechanisch geht das nicht,
die Energie ist gequantelt. Bei kleinen Temperaturen reicht die thermische Eergie nicht aus, um die Schwingung anzuregen,
der Freiheitsgrad ist "eingefroren". |
 |
Woran erkennt man das Problem? Wie beobachtet man die Zahl der Freiheitsgrade experimentell? |
 |
Um das zu verstehen, formulieren wir zunächst den ersten Haupsatz der Thermodynamik in der üblichen mathematischen Form: |
| |
|
|
 |
Mit dU=Änderung der inneren Energie U des betrachteten Systems, dQ=zugeführte
(differentiell kleine) Wärmeenergie, dW=nach außen geleistete (differentiell kleine) Arbeit
|
 |
Das ist der Energieerhaltungssatz
unter Einschluß der Wärmeenergie. In Worten besagt obige Gleichung |
|
 |
Die (differentiell kleine) Änderung
der im System vorhandenen inneren Energie ist gleich der (differentiell kleinen) zugeführten Wärmeenergie
minus der nach außen geleisteten (differentiell kleinen) Arbeit. |
|
 |
Statt dem differentiellen "d" hätten wir auch das "Änderungs"
D nehmen können, aber in der gewählten Form wird klar, daß die dU,
dQ usw. mit Ableitungen der eigentliche Funktionen nach den Variablen zusammenhängen. |
|
 |
Die nach außen geleistete Arbeit resultiert in der Regel aus einer Volumenänderung
- der paradigmatische Kolben bewegt sich in einem Zylinder, z.B. in der Wärmekraftmaschine Benzin- oder Dieselmotor. |
| |
|
|
 |
Hier ist die Illustration zum 1. Hauptsatz. Links ganz allgemein, rechts in der üblichen
technischen Ausführung mit einem Kolben, der sich in x -Richtung bewegen kann. |
 |
Diese Formulierung (in etwas anderer Weise im Jahre 1842) war eine monumentale
Leistung, verbunden mit den Namen Robert Mayer und J. P. Joule; außerdem noch mit einer interessanten
Geschichte. |
 |
Schauen wir uns ein einfaches Beispiel an: Einem (perfekten) Kristall wird ein
bißchen (dQ) Wärme zugeführt. |
|
 |
Die nach außen geleistete Arbeit ist immer Kraft mal Weg, oder umgeschrieben,
Druck p mal Volumen V. Da wir unseren Kristall nur "rumliegen" lassen, ändert
sich der Druck nicht, der Kristall wird sich aber etwas ausdehnen, d.h. das Volumen ändert sich. |
|
 |
In differentieller Form erhalten wir für die geleistete Arbeit dW |
| |
|
 |
Daß hier wirklich Arbeit geleistet wird, kann man sofort sehen, wenn man
gedanklich versucht, den Kristall an der Volumenausdehnung zu hindern. Man müßte dazu beachtliche Kräfte
aufwenden und den Kristall dann unter sehr hohem Druck halten. Oder, andersherum, der sich ausdehnende Kristall kann eine
große Kraft auf einem sehr kleinen Weg wirken lassen, d.h. etwas Arbeit leisten. |
|
 |
Noch einfacher wird es, wenn wir statt einem Kristall ein Gas nehmen: Alle Wärmekraftmaschinen
- von der alten Dampfmaschine über den Ottomotor zum Düsentriebwerk - beziehen die nach außen geleistete
Arbeit aus der Ausdehnung von Gasen bei Erwärmung. |
|
 |
Läßt man Ausdehnung nicht
zu, geht der Druck hoch. Dabei wird aber keine Arbeit nach außen geleistet.
In diesem Fall gilt dW=0 und der erste Hauptsatz reduziert sich für den Fall konstanten Volumens auf
|
| |
|
|
 |
Die gesamte zugeführte Wärme geht in die Erhöhung (oder, bei Vorzeichenwechsel,
Erniedrigung) der inneren Energie. |
 |
Für unseren Kristall jedoch, den wir i.a. bei konstantem Druck belassen und
dafür eine Volumenausdehnung akzeptieren, schreibt sich der erste Haupsatz wie folgt: |
| |
|
dU |p=const = dQ – p · dV |
|
|
 |
In Worten: Die (differentiell kleine) Änderung
der im System vorhandenen inneren Energie ist gleich der (differentiell kleinen) zugeführten Wärmeenergie
minus Druck mal der (differentiell kleinen) Änderung des Volumens. |
| | |
|
|
Die Enthalpie als neues Energiemaß
|
| |
|
 |
Bei sehr vielem, was wir mit festen
Körpern
so treiben, bleibt der Druck konstant - ganz im Gegensatz zu Gasen! Um in vielen Beziehungen den Term –pdV
nicht immer mitschleppen zu müssen, führt man eine neue Größe
ein, die aus schreibtechnischen Gründen unter diesen Bedingungen anstelle der (inneren) Energie verwendet wird, nämlich
die Enthalpie
H. |
|
 |
Das Wort "Enthalpie" hat
Kammerling-Onnes (der Entdecker der Supraletung) 1909
geprägt; es stammt (wie üblich) aus dem Altgriechischen und bedeutet in etwa "Erwärmung". |
|
 |
Die Enthalpie ist damit eine Energieform - so wie die
kinetische, potentielle oder innere Energie auch; ihre Einheit ist 1 J. Sie hängt mit der inneren Energie über
eine einfache Definitionsgleichung zusammen: |
|
|
|
 |
Formulieren wir den ersten Hauptsatz nun mit der Enthalpie,
müssen wir als erstes dH bilden; das ist in diesem Fall das totale Differential
der Enthalpie H. Wir erhalten |
|
|
|
dH = dU + p · dV + V · dp
|
|
 |
Mit V · dp = 0, weil wir ja
konstanten Druck annehmen, und dem ersten Hauptsatz (dU = dQ – p ·
dV) ergibt sich dann |
|
|
|
 |
Die gesamte zugeführte Wärme geht jetzt also in die
Erhöhung (oder, bei Vorzeichenwechsel, Erniedrigung) der (inneren) Enthalpie
des Materials. |
|
 |
Wir können die Enthalpie also als die um die Wärmeausdehnung
korrigierte innere Energie betrachten. |
 |
Das führt sofort auf eine wichtige Konsequenz: |
|
 |
Da die Wärmeausdehnung bei Festkörpern i.a. klein ist, sind Enthalpie
und (innere) Energie dann fast identisch. Man sagt im Sprachgebrauch deshalb oft "Energie", wenn man eigentlich "Enthalpie"
meint - und macht dabei auch keinen großen Fehler. Für Gase gilt dies aber nicht! |
| |
|
 |
Aus dem 1. Hauptsatz ergeben sich sofort die Wärmekapazitäten
C aller Materialien. Sie sind definiert als der (Differential)quotient aus der
(differentiellen) Zunahme der Wärmenergie und der (differentiellen) Änderung der Temperatur, in anderen Worten |
| |
|
|
 |
für den jeweiligen Körper mit der Masse M . |
 |
Die Wärmekapazität läßt sich leicht messen; was wir erhalten,
wird davon abhängen, ob wir bei Zufuhr der Wärme das Volumen konstant halten
(durch entsprechenden Aufbau äußeren Drucks) oder den Druck. |
|
 |
Die entsprechenden Werte (mit Index V oder p für die jeweils
konstant gehaltene Zustandsvariable) für einen Körper der Masse M sind dann unter Verwendung des
1. Hauptsatzes und der innerer Energie U bzw. Enthalpie H gegeben durch |
| |
|
 |
Irgendwelche Messwerte für irgendwelche Massen M sind natürlich
keine sinnvollen Materialparameter. |
|
 |
Wir brauchen spezifischen Wärmen
c,
also zum Beispiel die Wärmekapazität pro Masseneinheit M. Das ist dann
einfach |
| |
|
 |
Die innere Energie oder besser Enthalpie für einen Kristall kennen wir aber
schon; es galt |
|
| U Kristall | = |
N · ½ · f · kT |
|
|
|
 |
Mit N = Zahl der Atome im Kristall. |
 |
Mit
AV
= Avogadrokonstante =
Zahl der Teilchen (= Atome oder Moleküle) in einem Mol
einer Substanz = 6,022 · 1023, definiert man die sog. Gaskonstante
R = k · AV. Damit ergibt sich noch eine spezifische Wärmekapazität, nämlich die äußerst
sinnvolle molare Wärmekapazität
von 1 mol eines beliebigen Kristalls, unabhängig von der Temperatur. Wir erhalten immer |
| |
| cKrist, mol | = cp, mol = |
½ · 6 · R = 3R |
|
|
 |
Das ist die lange vor der Rechnung experimentell gefundene Dulong-Petitsche
Regel. |
|
 |
Die simple statistische Behandlung der Wärme gab die Formel dazu. Sie
ist bemerkenswert, sagt sie doch, daß alle
Kristalle - ob mit einfachem oder kompliziertem Gitter, ob mit einfacher oder komplizierter Basis, ob mit mit leichten
oder schweren Atomen in der Basis - dieselbe
spezifische Wärmekapazität haben, wenn man sie auf 1 mol bezieht. |
 |
Ob diese Regel immer
stimmt, kann man experimentell prüfen. Im 19. Jahrhundert lag man bei der "Nachprüfung"
nicht so schlecht (so wurde die Dulong-Petitsche Regel ja gefunden), aber im 20. Jahrhundert konnte man zum ersten
Mal richtig tiefe Temperaturen machen. |
|
 |
Und siehe, es stellt sich heraus, daß die molaren Wärmekapazitäten für
alle festen Stoffe mit abnehmender Temperatur nicht mehr konstant bei 3 R lagen,
sondern kleiner wurden und sogar gegen Null tendierten - im Link ist eine Illustration
dazu. |
|
 |
Erst Albert Einstein hat, wie oben schon gesagt, dieses Rätsel als erster erklärt (quantitativ, mit einer Formel), indem er die
Quantenmechanik ins Spiel brachte. |
|
|
 |
Zusammenfassend halten wir fest: |
|
 |
Der erste Hauptsatz stellt fest, daß nur thermodynamische
Prozesse, bei denen die Energie erhalten bleibt, in der Natur vorkommen können.
Er verbietet aber beispielsweise nicht, daß aus einem Wärmereservoir (z.B. den Meeren) mechanische Arbeit entnommen
werden kann, wobei sich das Reservoir abkühlt. Auch die Umkehrung
des Gedankenversuchs zum thermischen Gleichgewicht wäre prinzipiell möglich: Ein lauwarmer Körper wird
an einem Ende heiß, am anderen kalt. |
|
 |
Mit dem 1. Hauptsatz allein können wir noch keine Gleichgewichte bekommen. Wir
brauchen weitere Prinzipien, wir brauchen den 2. Hauptsatz! |
| |
|
© H. Föll (MaWi 1 Skript)