|
Die Darstellung der Bindungsenergie - genauer der potentiellen Energie des Bezugsatoms
- als Funktion des Abstands von Bindungspartnern - ist, in jeder Näherung, eine außerordentlich nützliche
Graphik; im Unterkapitel 2.2.2 sind wir diesem Konzept schon begegnet. Jede solche
Darstellung die ein Minimum der potentiellen Energie besitzt, nennen wir "Potentialtopf"
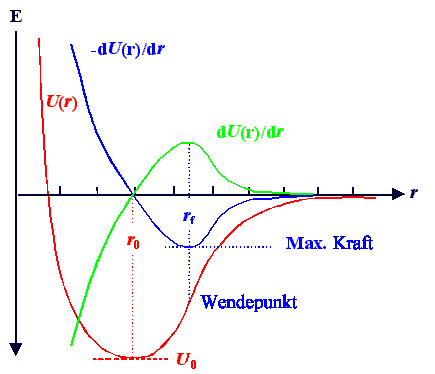
Der Potentialtopf zeigt - zusammen mit seinen Ableitungen - sofort wesentliche Elemente der Bindung: |
| |
|
|
 |
Die Bindungsenergie
U0, gegeben durch die Tiefe des Potentialtopfes, |
|
 |
Den Gleichgewichtsabstand
r0, definiert durch den Ort des Minimums. |
|
 |
Die Kraft
F, die auf das betrachtete Atom wirkt, wenn es einen beliebigen Abstand r vom Partner hat; sie
ist per definitionem gegeben durch |
| |
|
|
 |
Die Kraftkurve ist also die (negative) Ableitung der Potentialkurve. Bei r0
geht sie durch Null - wie das sein muß. |
|
 |
Die maximale Kraft
Fmax die man braucht um die Verbindung zu lösen; gegeben durch das Maximum der Kraftkurve, d.h. durch die Bedingung
|
| |
|
 |
Dazu wollen wir eine kleine Übungsaufgabe machen |
| |
|
 |
Hat man viele Atome, werden sie sich solange bewegen, bis alle im Minimum eines Potentialtopfs
sitzen, d.h. (im Mittel) keine Kräfte von den Nachbaratomen mehr spüren |
|  |
Das kann man sich in einem "advanced" Modul mal per
Simulation anschauen. Mit in bißchen Spielen kann man Kristalle bilden und wieder schmelzen! |
 |
Die Potentialtopfkurve kann aber noch mehr veranschaulichen. Wenn die Atome
nicht vollständig ruhig beim Gleichgewichtsabstand r0 sitzen, sondern um diese Gleichgewichtslage
vibrieren; tun sie das im Potentialtopfbild, indem sie wie eine Kugel in einem wirklichen
Topf mit der entsprechenden Gestalt, die Wände hoch- und runterlaufen |
| |
|
 |
Dabei kann - es gilt die Quantentheorie - nicht jede beliebige
Schwingung auftreten, sondern nur solche die bestimmte, durch die Lösung der entsprechenden Schrödingergleichung
gegebene Energien haben können. Die damit verbundenen Energien kann man als Energieniveaus
(die bei Atomen wegen der großen Masse dicht benachbart sind) in den Potentialtopf einzeichnen und der Graphik folgende
Informationen entnehmen: |
|
 |
Die
Frequenz der Schwingung; einfach aus der Masse und der durch
den Potentialtopf gegebenen Rückstellkraft. |
|
 |
Die Amplitude der Schwingung als Differenz der beiden
Extremabstände rmax und rmin. |
|
 |
Die ungefähre Schmelztemperatur (oder
Zersetzungstemperatur). Sie ist erreicht, wenn die thermische Energie, die ja nichts anderes ist als die in den Schwingungen
sitzende Energie, ungefähr gleich der Bindungsenergie wird. Denn dann ist das Atom bei rmax
schon so weit vom Partner weg, daß es kaum mehr eine Rückkehrkraft spürt. |
|
 |
Die Größenordnung der thermischen Ausdehnung.
Durch die Asymmetrie des Potentials ist das Atom insbesondere bei großen Amplituden im Mittel weiter vom Partner entfernt
als r0 - der Bindungsabstand wird länger; das Material dehnt sich beim Erwärmen (= mehr
Schwingungen mit hoher Energie) aus. |
 |
Quantitative Beziehungen zu all diesen Größen werden in Kapitel 2.4 abgeleitet. |
|
|
|
© H. Föll (MaWi 1 Skript)