2.2.2 Vom Molekül zum Kristall - Potentialbild und Madelungkonstante

Bindungspotential und Potentialtopf

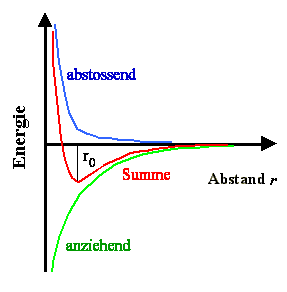
	Es ist nicht nur lehrreich und eingängig, sondern an dieser Stelle auch sinnvoll und weiterführend, sich zunächst die idealisierten Vorgänge bei der Ionenbindung in abstrahierter Form graphisch vor Augen zu führen. Dazu tragen wir in ein Energie - Abstands Diagramm die relevanten Energieverläufe ein. Wir tun das zunächst nur für die Ionen.
		Dabei ist als erstes die potentielle Energie der Coulombanziehung (das elektrostatische Potential) d.h. die Energie der einen Ladung im Feld der anderen, zu berücksichtigen. Sie muß im Unendlichen = 0 sein und für den (hypothetischen) Abstand 0 mit 1/a gegen –¥ streben. Wir können diese Kraft ohne weiteres berechnen; sie ergibt sich aus der vorstehenden Kraftformel. Das anziehende Potential verläuft demnach mit
		Uan  =  –  A r
		Wobei wir die Konstante einfach mit A kennzeichnen.
		Weiterhin müssen wir nun die Abstoßung in Betracht ziehen, die sich ergibt, wenn sich die Ionen zu nahe kommen. Denn sobald sich die Elektronenhüllen zu nahe kommen, oder sich gar durchdringen, sind die abstoßenden Kräfte zwischen den vielen Elektronen der inneren Schalen viel größer als die Anziehung auf der Basis nur einer Elementarladung.
		Genauer betrachtet müßte man jetzt Quantenmechanik treiben. Denn für die Elektronen des Li ist im Inneren des F-Ions kein Platz. Salopp betrachtet kann man sich vorstellen, daß selbst ohne die elektrostatische Abstoßung, die Heisenbergsche Unschärferelation und das Pauli-Prinzip dafür sorgen, daß man nicht allzuviele Elektronen in einem gegeben Volumen unterbringen kann
	Leider haben wir keine Chance, die dadurch auftretenden Kräfte auszurechnen oder das zugehörige Potential zu ermitteln. Aber wir können uns fragen, was wir aus allgemeinem Wissen dazu sagen können. Das wird für alle praktischen Betrachtungen ausreichen (müssen).
		Zunächst kann man annehmen, daß die abstoßende Kraft ziemlich ungerichtet ist, denn die mittlere Elektronenverteilung in den Ionen ist halbwegs kugelsymmetrisch (die gerichteten p-Orbitale sind immer gefüllt).
		Klar ist auch, daß die abstoßende Kraft nicht spürbar ist, wenn die Ionen sich nicht unmittelbar berühren; für a > a0 wird diese Kraft also klein sein und mit wachsendem Abstand schnell verschwinden.
		Genau beim Gleichgewichtsabstand wird abstoßende Kraft = Coulombkraft sein müssen, denn a0 ist ja gerade der Abstand bei dem in Summe keine Kräfte mehr wirken.
		Für a < a0 wird die abstoßende Kraft steil gegen +¥ streben. Wir wissen das aus dem tägliche Leben, denn es ist bekanntlich sehr schwer, zwei (nichtbiologische) Körper ineinander zu schieben. Wo ein Körper ist, kann kein anderer sein, das wußte schon Archimedes. Und das ist so, weil wir sonst Atome auf ein Volumen konzentrieren würden, das erheblich kleiner ist, als die Summe der beiden individuellen Volumina. Eine merkliche Volumenreduzierung und damit Dichteerhöhung ist nur bei extremsten Drücken möglich, wie sie im Innern von manchen Sternen vorliegen.
	Wir können also durchaus einen ungefähren Verlauf der abstoßenden Energie aufzeichen; auf Details wird es uns hier noch nicht ankommen. Die Überlagerung der beiden Potentialkurven wird dann die potentielle Energie der Ionenbindung als Funktion des Abstandes darstellen. Das sieht so aus:

	Die gesamte potentielle Energie, die ein Ion bei Annäherung an das Bezugsion spürt ergibt sich durch direkte Addition der beiden Kurven. Diese Kurve des Bindungspotentials - man nennt diese Kurve auch Potentialtopf - ergibt sich dann automatisch so, daß:
		Im ¥ keine Kräfte wirken. daraus folgt, daß die Potentialkurve horizontal verläuft (Kräfte F ergeben sich aus einem Potential U(r) immer durch Differenzieren:
		F  =  –  ÑU(r) Fx  =  –   dU dx   Fy  =  –   dU dy   Fz  =  –   dU dz
		Da bei Annäherung an den Abstand r = 0 (entspräche der Verschmelzung der Ionen) die abstoßende Kraft (sie muß in der gewählten Konvention ein negatives Vorzeichen haben) extrem groß wird, muß das Potential steil nach oben laufen.
		Beim Gleichgewichtsabstand r0 (oder a0, wir verwenden beide Symbole), der ja so definiert ist, daß auf das Ion keine Kräfte mehr wirken, hat das Potential ein Minimum, d.h. .
		F(r = r0)  =  0
		Die Tiefe des Potentialtopfes gibt dann direkt die Bindungsenergie an. Denn die Bindungsenergie war die Arbeit, die nötig ist um das Teilchen ins ¥ zu bringen.
	Um dieses Potentialtopfbild besser nutzen zu können, muß es in Formeln gefaßt werden. Dazu fehlt nur eine Formel für das abstoßende Potential. In einfachster, aber ausreichender (mathematischer) Näherung beschreiben wir die Abstoßung einfach durch
		Abstoßendes Potential = Uab  =  B rm
		Dabei ist zunächst offen ist, wie groß die Parameter B und m sind. Da aber die abstoßende Kraft sich sehr viel schneller mit r ändert als es die anziehende tut, wird m >> 1 sein; Werte von 8 - 12 sind realistisch.
	Damit erhalten wir für das Bindungspotential zweier Ionen die allgemeine Potentialformel
		UBindg  =  –  A r  +  B r m

	Das sieht nicht sehr nützlich aus, da 3 freie Konstanten in der Formel stehen: A, B und m.
		Für A können wir jedoch sofort den Wert aus dem Potential zwischen zwei geladenen Teilchen einsetzen. A = e1 · e1/4p ·e0.
		Die Parameter B und m können wir zumindest durch physikalisch meßbare Größen ausdrücken, denn es gilt mit den obigen Bedingungen
		UBin (r = r0)  =  Bindungsenergie EBin dU dr(r = r0)  =   0
	Unsere Potentialformel läßt sich damit so umschreiben, daß nur noch EBin und r0 als Parameter vorkommen. Wir werden von dieser Möglichkeit noch reichlich Gebrauch machen.

	Vom Molekül zum Festkörper
	Wir machen jetzt gedanklich aus einem Molekül mit Ionenbindung - z.B. wieder unser LiF - einen Festkörper (es wird automatisch ein Kristall).
		Dazu nehmen wir das Molekül und addieren zunächst noch ein weiteres F– und Li+ Ion. Wir brauchen beide, wenn wir einen ungeladenen Körper produzieren wollen.
		Um das ganze einfach zu halten, beschränken wir uns vorläufig noch auf eine eindimensionale Welt; d.h. wir können weitere Ionen nur entlang der Bindungsrichtung r zuführen. Damit ist klar, daß wir das zweite F– Ion an das schon vorhandene Li+ Ion anlagern, und das 2. Li+ Ion an das schon vorhandene F– Ion.
		Das Ergebnis sieht dann so aus

	Wenn wir jetzt das Bindungspotential für eines der 4 Ionen betrachten, z.B. für das äußere Li+ Ion, müssen wir für das elektrostatische Potential die Wechselwirkung mit allen drei verbleibenden Ionen einsetzen. Den Nullpunkt wählen wir beim entferntesten F – Ion; es gilt also für diesen eindimensionalen Fall:
		ULi + (r)  =   –   A  r   +  A  r  –  r0   –   A  r  –  2r0
		Man kann diesen Ausdruck noch vereinfachen, wir aber wollen gleich für den dreidimensionalen Fall verallgemeinern.
		Dazu betrachten wir zunächst noch eine zweidimensionale Anordnung der Ionen. Die einzige mögliche Form die zeichnerisch sinnvoll ist sieht so aus:

	Denken wir uns das ganze noch dreidimensional und nehmen wir dann gedanklich irgendein Ion aus dem Kristall heraus (mathematisch geht das; eine physikalische Umsetzung ist nicht nötig), müssen wir über alle Einzelpotentiale summieren.
		Statt der Formel mit den Summanden wie oben bekommen wir eine Summe mit N - 1 Summanden, falls der Kristall aus N Ionen besteht.
		Wie wir summieren müssen, wird dabei davon abhängen, wie die Atome räumlich angeordnet sind. Das kann, aber muß nicht so sein wie im Bild gezeigt.
		Bei mit bloßem Auge sichtbaren Kristallen liegt N in der Gegend von 1020; man kann also gleich zu ¥ viel Summanden gehen (und dann integrieren statt summieren).
		Das ganze ist offenbar nur sinnvoll, wenn die Summen gegen einen endlichen negativen Wert konvergieren. Das müssen sie aber, weil sonst der Kristall nicht zusammenhalten würde.
	Wenn man das alles macht, erhält man ein verblüffend einfaches und ganz allgemeines Ergebnis. Die Potentialformel von oben ändert sich nur ganz wenig, sie lautet jetzt
		UBindg  =   – am · A r + B r m

	Es wird also nur der anziehende Teil durch Multiplikation mit einer Konstanten etwas modifiziert. Der abstoßende Teil ist nicht betroffen, da die Kräfte so schnell abfallen, daß Ionen in größerem Abstand gar nicht "gespürt" werden.
		Die Konstante am, die sich aus der Summation ergibt, heißt Madelungkonstante, nach dem Festkörperphysiker Madelung.
		Der exakte Wert der Madelungkonstanten hängt natürlich von den Ionensorten und den damit verknüpften Bindungslängen sowie der dreidimensionalen Anordnung ab.
		Typische Werte für einige Ionenkristalle sind
		Kristall (Molekülformel) Kristalltyp (kommt später) Madelungkonstante am NaCl kubisch-flächenzentriert 1,748 CsCl kubisch-raumzentriert 1,763 ZnS kubisch-diamant 1,638 ZnS hexagonal 1,641 CaCl kubisch-primitiv 2,365 CaF2 kubisch-flächenzentriert 5.039 CdCl2 hexagonal 2,244 ZnO hexagonal 1,498 SiO2 hexagonal 2,219 Al2O3 Rhomboedrisch 4,172

	Die Ionen sind also in einem Kristall stärker gebunden als im Molekül. Das muß auch so sein, denn sonst würde sich aus Molekülen oder Ionen nie ein Festkörper formen.
		Stärkere Bindung (positive Madelungkonstante) heißt ja, daß Energie frei wird, wenn sich aus einzelnen Molekülen ein Festkörper bildet (Beim Gefrierpunkt). Und noch gehen wir davon aus, daß immer der energetisch niedrigste Zustand begünstigt wird.
		Eine negative Madelungkonstante würde bedeuten, daß man Energie braucht, um einen Festkörper zu bilden - er würde also nicht stabil sein.
	Wer es noch genauer wissen möchte (und vielleicht selbst probieren will, wie leicht oder schwer es ist, Madelungkonstante auszurechnen), betätigt den Link.
		Fragebogen Multiple Choice Fragen zu 2.2.2

© H. Föll (MaWi 1 Skript)