Madelungkonstante

	Wir berechnen mal die Madelungkonstante für die einfachsten Ionenkristalle, z.B. für NaCl. Wie dieser Kristall aussieht, kann man im Link betrachten
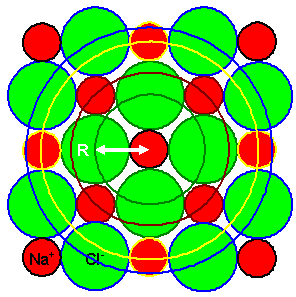
		Im Zentrum des Koordinatensystem sitzt also ein Na+ Ion. Es hat 6 Cl– ionen als nächste Nachbarn im Abstand R = a/2; dabei ist a die Gitterkonstante.
		Wie das halbwegs maßstabsgetreu und zweidimensional aussieht, zeigt das folgende Bild.
		Die zweitnächsten Nachbarn sind dann 12 Na+ Ionen im Abstand 2½ · R.
		Es folgen 8 Cl– ionen im Abstand 3½ · R, dann 6 Na+ ionen im Abstand 2 · R, und so weiter und so fort.
	Die zugehörigen potentiellen Energien betrachten wir uns gleich in einer strukturierten Tabelle
		Nachbartyp Zahl Abstand Typ Potential Formel 1. 6 Cl– R anziehend U  =   –   e2 4pe0R  ·  6 · 2–½ 2. 12 Na+ 2½ · R abstoßend U  =   +   e2 4pe0R  ·  12 · 2–½ 3. 8 Cl– 3½ · R anziehend U  =   –   e2 4pe0R  ·  8 · 3–½ 4. 6 Na+ 4½ · R abstoßend U  =   +   e2 4pe0R  ·  6 · 4–½ 5. ... ... ... ...
	Damit ist die gesamte potentielle Energie
		U  =    –    e2 4pe0R æ ç è 6 1½  –    12 2½  +  8 3½   –   6 4½  +  ..... ö ÷ ø                              =     –   e2 4pe0R  · a
	Der Ausdruck in der Klammer ist die Madelungkonstante a.
		Alles, was wir noch zu tun haben ist das Bildungsgesetz der unendlichen Reihe zu finden, und dann die mathematische Aufgabe der Aufsummierung zu lösen.
		Das ist zwar nicht unbedingt einfach, aber machbar, und wir finden a = 1.7476. Leider konvergiert die Summe nur langsam; die 4 oben gezeigten Terme ergeben z.B. erst – 0.866.
	Für kompliziertere Kristalle wird die Berechnung der Madelungkonstanten zwar noch nicht unbedingt zur Lebensaufgabe, aber doch zu einer anspruchsvollen mathematisch-geometrischen Übung.

Mit Frame

2.2.2 Vom Molekuel zum Kristall - Potentialbild und Madelungkonstante

© H. Föll (MaWi 1 Skript)