2.2.3 Kovalente Bindung

Bei der Ionenbindung war die Ausgangslage, daß sich verschiedene Atome, die zum einen zu wenige und zum anderen zu viele Elektronen haben (immer bezogen auf gefüllte Schalen) zusammentun, und dabei Elektronen von einem Partner zum andern transferiert werden (siehe auch Quantenmechanik-Skript).

Kovalente Bindungen in Reinkultur liegen vor, wenn zwei Atome, die beide zu wenig Elektronen haben, sich verbinden. Beispiele sind

Die Halogenide in Gasform: F₂, Cl₂, Br₂, usw.

Viele typischen Gase: O₂, N₂, NH₃ (Ammoniak), CO₂, usw.

Festkörper wie z.B. Si, Ge, C (in der Form des Diamanten), GaAs (Galliumarsenid) und andere.

Das Grundprinzip ist immer dasselbe: Die Atome teilen sich den Mangel; dabei geht es ihnen viel besser als wenn jedes seinen Elektronenmangel alleine bewältigen muß.

Korrekt ausgedrückt bedeutet dies, daß sich Orbitale (in der Regel p-Orbitale), die nur teilweise besetzt sind, sich beim Näherkommen überlappen und, je nach Vorzeichen, ein gemeinsames Orbital bilden können, das gleichberechtigt zu beiden Atomen gehört, und das es in zwei Varianten gibt.

In erster Näherung haben wir eine Überlagerung der beiden individuellen Orbitalwellenfunktion y₁ und y₂ zu einem Molekülorbital y_Mol in der Form

y_Mol	=	A₁ · y₁ ± A₂ · y₂

Die A_i sind Konstanten; eine davon ergibt sich die sich aus der Normierungsbedingung, die andere müßte aus einer Lösung der Schrödingergleichung für das Molekül ausgerechnet werden.

Nur eines der beiden möglichen Summenorbitale führt zur Energieabsenkung und damit zur Bindung. Das andere führt zur Energieerhöhung; es ist "antibindend". Diese antibindende Orbitale sind zwar nicht unwichtig (schließlich will man eine Verbindung auch wieder lösen können; dies geschieht bei Energiezufuhr durch Anheben der Elektronen in das antibindende Orbital), sollen uns aber hier nicht weiter interessieren.

Aus Sicht des Einzelatoms kann das (gemeinsame und bindende) Orbital jetzt voll besetzt sein, den es sind ja zwei Elektronen da, d.h. die Edelgaskonfiguration ist erreicht.

Kovalente Bindungen können dabei zwischen gleichartigen Atomen (z.B. C - C) oder verschiedenen Atomen auftreten (z.B. Si - C oder C - H).

Die entstehenden Moleküle werden durch die gerichtete kovalente Bindungen eine durch die Symmetrie der beteiligten Orbitale genau festgelegte räumliche Geometrie erhalten.

Dazu zwei schematischen Darstellungen; das schematische Schalenbild wie zuvor und die Bindung im Orbitalbild

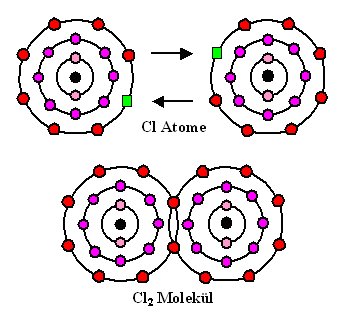Das stark vereinfachte Schema im Schalenbild.

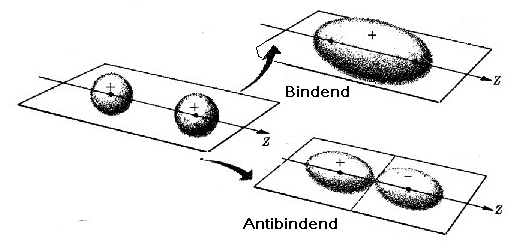Gezeigt sind die bindenden und antibindenden Orbitale bei Überlappung von
s - Orbitalen (keine Richtungsabhängigkeit der Bindung).

Die Orbitaldarstellung führt natürlich viel weiter als die Schalendarstellenung; insbesondere erkennt man sofort Bindungsrichtungen, und auch Dinge wie Doppel- und Dreifachbindungen lassen sich gut darstellen. Im Link gibt es besonders wichtige Beispiele.

Ein letzter Punkt muß noch eingeführt werden, um die Möglichkeiten der Quantentheorie für kovalente Bindungen voll auszuloten und insbesondere die für uns wichtige Si - Si (und damit auch die chemisch ähnliche C - C) Bindung verstehen zu können. Es handelt sich um das Phänomen der Hybridisierung.

Einfach gesagt, bilden sich dabei aus s- und p - Orbitalen neue Misch- oder eben Hybridorbitale.

Das ist erlaubt, denn die Linearität der Schrödingergleichung führt grundsätzlich dazu, daß wenn y₁, y₂, usw. Lösungen der Schrödingergleichung sind, auch jede Linearkombination dieser Lösungen, z.B. y = ay₁ + by₂ die entsprechende Schrödingergleichung löst (wobei a und b beliebige Koeffizienten sind, die allerdings der Normierungsbedingung genügen müssen).

Bei einem Einzelatom werden die Elektronen jedoch von dieser Möglichkeit keinen Gebrauch machen, weil sich die Energie dabei erhöht. Anders jedoch bei Bindungen. Durch die Bildung geeigneter Hybridorbitale läßt sich die Überlappung der Orbitale mit anderen Atomen maximieren und damit Energie gewinnen.

Insbesondere bei C, Si, Ge, wäre es günstig, die Orbitale so zu rearrangieren, daß 4 Keulen gleichverteilt in den Raum hinausragen; jede mit einem Elektron besetzt. Damit ist optimaler Andockplatz für die 4 benötigten Partner geschaffen und größtmögliche Symmetrie erzielt.

Passende Orbitale lassen sich durch Kombination der s- und p- Orbitale darstellen. Die Linearkombinationen

y₁ = ½	(s +	p_x +	p_y +	p_z)
y₂ = ½	(s +	p_x –	p_y –	p_z)
y₃ = ½	(s –	p_x +	p_y –	p_z)
y₄ = ½	(s –	p_x –	p_y –	p_z)

(mit den Bezeichnungen s und p für die entsprechenden Wellenfunktionen) bilden genau die gewünschten 4 "sp³ - Hybridorbitale"; sie sind mit je einem Elektron besetzt.

(Die Nomenklatur weicht hier etwas von der alten Schreibweise ab: Bei Einzelorbitalen bezeichnet die hochgestellte Zahl die Zahl der Elektronen, die im konkreten Fall das Orbital besetzen; bei Hybridorbitalen aber die Zahl der Orbitale, die an der Hybridisierung teilnehmen - so ist sie nun mal, die Chemie!)

Die bildliche Darstellung sieht so aus:

	Links die Kugel - und Keulendarstellung der reinen s- und p- Orbitale; rechts die sp³ Hybridorbitale.
		Links wäre das s - Orbital mit 2 Elektronen voll besetzt; in den 8 Keulen der p - Orbitale sind die restlichen 2 Elektronen der Elemente C, Si, Ge. Keine gute Anordnung um 4 weitere Atome zu binden.
		Im den sp³ Hybridorbitalen sind dagegen 4 mit je einem Elektron besetzt Keulen vorhanden. Die Orbitale liegen nicht mehr in Richtung der Seitenkanten eines Würfels, sondern zeigen vom Zentrum in die Ecken eines gleichseitigen Tetraeders mit dem Tetraederwinkel 109,5⁰.
		Setzt man wie mit einem Steckbaukasten jetzt viele solche Atome entlang der Keulenachsen zusammen, entsteht zwingend ein Kristall mit spezifischer Struktur - der Diamantstruktur.

Ohne in mehr Details zu gehen, können schon folgende Schlußfolgerungen gezogen werden

Die Bindungskräfte sind im allgemeinen stark gerichtet, denn kovalente Bindungen liegen nur bei p- und d-Orbitalen vor und sind dann im wesentlichen nur entlang der Orbitalachse wirksam.
(s-Orbitale, die nur mit einem Elektron besetzt sind, fallen, abgesehen vom H₂ Molekül, immer unter sie Rubrik "ein Elektron zuviel", und damit unter die Metallbindung).

Falls mehr als ein Elektron fehlt, wird eine Zweierbeziehung nicht ausreichen um alle Partner glücklich zu machen - es werden so viele Partner benötigt wie Elektronen fehlen. Daraus lassen sich allgemeine Strukturbildungsprinzipien für die Elemente mit 1 - 4 fehlenden Elektronen ableiten, die wir aber hier nicht näher betrachten wollen sondern in einem extra Modul.

Obwohl sich die Atome jetzt etwas "durchdringen" (ihre Elektronenwolken müssen sich ja überlappen), werden wieder erhebliche abstoßende Kräfte auftreten, wenn der Bindungsabstand unterschritten wird. Wir können das zugehörige Potential entlang der Bindungsachse wieder mit folgender Gleichung approximieren

U_ab =	B r ^m

Wobei natürlich B und m für jedes Bindungspaar anders sein müssen.

Die anziehende Wirkung ist jetzt nur quantentheoretisch begreifbar und berechenbar - wir müssen die Schrödingergleichung für 2 Atome lösen.

Da wir das nicht können, argumentieren wir ähnlich wie bei der abstoßenden Kraft der Ionenbindung und landen bei der Näherungsformel für das anziehende Potential :

Anziehendes Potential = U_an	= –	A r ⁿ

Damit ergibt sich für das gesamte Bindungspotential entlang der Bindungsachse

U_Bindg =	–	A r ⁿ	+	B r ^m

Auch bei der anziehend Kraft gibt es jetzt einen Exponenten n, der erheblich größer als 1 sein wird. Trotzdem ergibt sich in der Überlagerung der Potentiale wieder ein Potentialtopf mit den gleichen allgemeinen Eigenschaften wie schon bei der Ionenbindung.

Insbesondere ist der Bindungsabstand r₀ und die Bindungsenergie direkt aus dem Potentialtopf ablesbar.

Wiederum lassen sich damit zwei der vier Parameter in obiger Gleichung substitutionieren.

Die Richtungsabhängigkeit der kovalenten Bindung sorgt für spezifische Strukturen nicht nur bei Verbindungen zwischen gleichen Elementen, sondern natürlich auch bei Verbindungen zwischen verschiedenen Elementen. Dabei kommt bei Verbindungen der Gruppe IV (C, Si, Ge, ...) insbesondere die sp³ Hybridisierung zum Tragen.

Die für die Hybridisierung notwendige Energie wird mehr als aufgewogen durch die hohe Symmetrie in dieser Anordnung. Um dies zu verstehen, machen wir eine kleine Übung und versuchen, Moleküle und Kristalle mit verschiedenen Hybridisierungen zu bilden.

Übung 2.2-4
Molekül- und Kristallbildung aus Bindungssymmetrien

Noch ein letztes Wort zur Nomenklatur. Überlappen sich die Keulen der p - Orbitale entlang ihrer Keulenachse, erhält man eine starke Bindung; sie heißt allgemein s-Bindung

Erfolgt der Überlapp (viel schwächer) senkrecht zur Keulenachse, spricht man von p-Bindung. Vor allem in den organischen Kohlenstoffverbindungen kommen beide Bindungstypen reichlich vor. Im Link sind noch einige Darstellungen wichtiger Moleküle mit kovalenter Bindung zu sehen und einige zusätzliche Besonderheiten der kovalenten Bindungen zu finden.

Fragebogen
Multiple Choice Fragen zu 2.2.3