4.10 The covalent bond

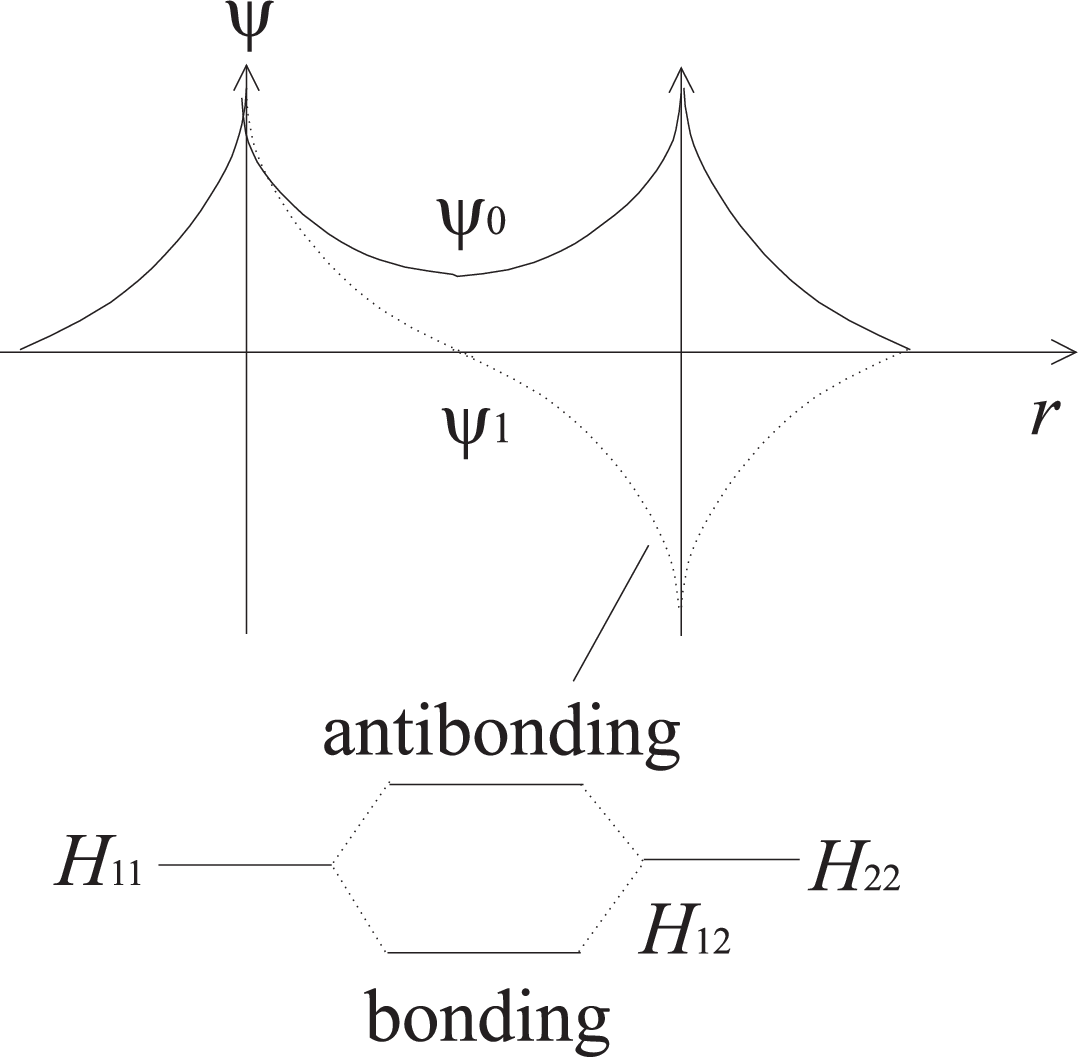
For a large number of molecules and solids the ground state is a singlet state of Eq. (4.68) and the descriptions of the wave functions following the Eq. (4.77)-(4.79) are a good approximation. Both electrons occupy the ground state \(\psi = \frac{1}{\sqrt{2}} \left(\Phi_1 + \Phi_2 \right)\) with opposite spin.

Since \(\Phi_1 = \Phi_2\) holds, \(\psi_0 =\frac{1}{\sqrt{2}} \left(\Phi_1 + \Phi_2\right)\) describes a state of accumulated charges between the cores of the atoms (cf. left side figure). This serves as an effective shielding of the positive core charges, leading to the lower energy of this state. This state is optimized to couple both atoms together; it is called the binding state. The binding energy is optimal when two electrons occupy this state (”electron pair binding”). In contrast to the binding state, the state \(\psi_1 = \frac{1}{\sqrt{2}} \left(\Phi_1 -\Phi_2\right)\) has a reduced electron density between the atom cores leading to an increased coulomb energy of this state; so it is called the antibonding state. Atoms with more than one electron have to occupy at least one antibonding state; this will reduce the binding energy. Further information you may find in the MaWi I script.

• Two electrons from two atoms of equal electronegativity share one state which is composed from atomic orbitals.

• Only atomic orbitals which are not fully occupied can use covalent bonding, since the binding orbital can only take two electrons.

• The corresponding binding energy is according to Eq. (4.76) defined by the overlap integral \(H_{12}\).

• Covalent bonding are directed, since this allows for the optimal overlap.

• To maximize the overlap and the number of bonds often the atoms form hybrid orbitals. The necessary excitation energy is overcompensated by the increase of the bonding energy. The hybridization allows for a great variety of mixed states which in consequence allows to optimize the overlap of atomic orbitals.

• The symmetry and structure of the crystals is dominated by this bonding with a strong direction.

The essence of the covalent bonding is the reduction of the coulomb repulsion of both atoms by increasing the electron density between the cores. But this allows a reduction of the energy only if the coulomb repulsion between the electrons does not overcompensate this effect.

© J. Carstensen (Quantum Mech.)