Magnetic properties of the two electron system: singlet and triplet state

4.9 Magnetic properties of the two electron system: singlet and triplet state

For each electron the spin can be \(+ 1/2\) or \(- 1/2\), leading to four possible states

\begin{equation*} \left|\uparrow \uparrow \right\rangle , \qquad \left|\uparrow \downarrow \right\rangle , \qquad \left|\downarrow \uparrow \right\rangle , \qquad \left|\downarrow \downarrow \right\rangle \qquad . \end{equation*}

(4.66)

According to the following table we can combine these states to get several states which differ in the values for the complete spin \(S\) and the component \(S_z\):


State	\(S\)	\(S_z\)	name	picture

\(\frac{1}{\sqrt{2}}\left( \left\|\uparrow \downarrow \right\rangle - \left\|\downarrow \uparrow \right\rangle \right)\)	0	0	singlet

\(\left\|\uparrow \uparrow \right\rangle \)	1	1	triplet

\(\frac{1}{\sqrt{2}}\left( \left\|\uparrow \downarrow \right\rangle + \left\|\downarrow \uparrow \right\rangle \right)\)	1	0	triplet

\(\left\|\downarrow \downarrow \right\rangle \)	1	-1	triplet

HINT:

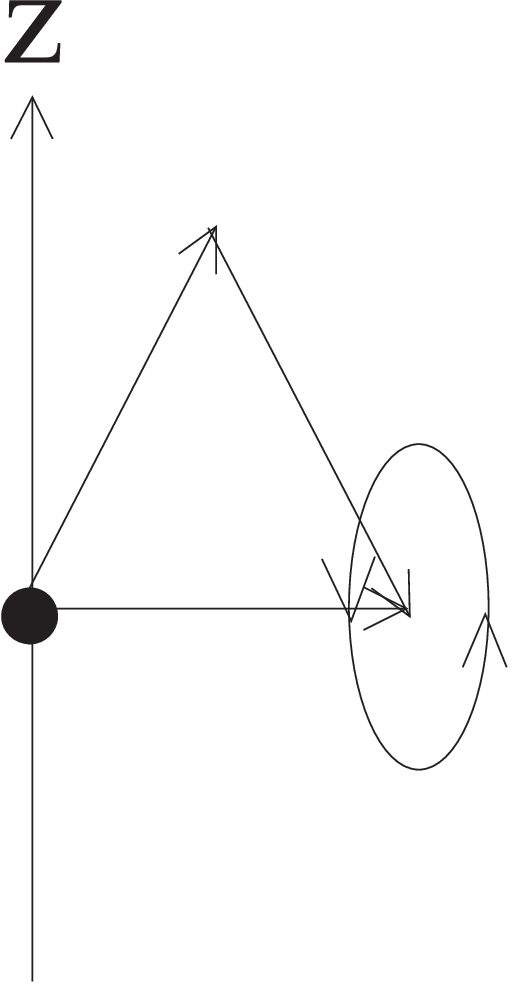
Spin add like vectors. In addition to the norm of the spin only one additional component (mostly referred to as the \(z\)-component) can be chosen. This may be interpreted as a rotation e.g. around the \(z\)-axis as illustrated in the right figure: two spins add to the complete spin leading to no effective \(z\)-component.

Since quantum mechanical particles are not distinguishable we already recognized that the symmetry for changing two indices is very important; exchanging the indices for a singlet state we get an additional minus sign which not occurs for a triplet state. Thus the singlet state is antisymmetric and the triplet state is symmetric when exchanging the indices. Always the complete wave function of the two electron state has to be antisymmetric; consequently the ”local” wave function of a singlet state must be symmetric and for a triplet state it has to be antisymmetric. Therefore we always find a magnetic momentum if the local wave function is symmetric in the local space when exchanging two indices and otherwise no magnetic momentum.
Following these considerations we will now solve the Schrödinger equation (4.64). Since we have a sum of two independent one electron Hamiltonians we can construct the complete solution as a product of solutions of

\begin{equation*} h \psi(r) = \epsilon \psi(r) \label{h_one_e} \end{equation*}

(4.67)

Let \(\psi_0(r)\) and \(\psi_1(r)\) be the solutions for the two lowest energy levels \(\epsilon_0\lt \epsilon_1\) of Eq. (4.67); the symmetric solution of the two electron state with the lowest energy is

\begin{equation*} \psi_s(r_1,r_2) = \psi_0(r_1) \psi_0(r_2), \qquad E_s = 2 \epsilon_0 \label{psi_sym} \end{equation*}

(4.68)

and the antisymmetric solution with the lowest energy is

\begin{equation*} \psi_t(r_1,r_2) = \psi_0(r_1) \psi_1(r_2) - \psi_0(r_2) \psi_1(r_1), \qquad E_t = \epsilon_0 +\epsilon_1 \label{psi_antisym} \end{equation*}

(4.69)

This leads to an energy gap between the singlet and triplet state of

\begin{equation*} E_s - E_t = \epsilon_0 - \epsilon_1 \end{equation*}

(4.70)

The singlet state will always be the ground state if the Coulomb coupling is negligible.
This singlet ground state corresponds perfectly to what we calculated in the last sections as the band structure of a solid:

Neglect the electron-electron coupling
Calculate single electron states
Fill all states with electrons, starting with the lowest energy level,
with two electrons of opposite spin
We will never find a magnetic momentum

Now we apply the Ritz’ variational method to get approximations for \(\psi_0\) and \(\psi_1\). As a test function we chose a linear combination of the atomic wave functions with the lowest energies of both atoms

\begin{equation*} \psi = \alpha_1 \Phi_1 + \alpha_2 \Phi_2 \end{equation*}

(4.71)

For the expectation value for the energy we find

\begin{equation*} \label{ritz_e} \epsilon' = \frac{\int \psi^* h \psi dV}{\int \psi^*\psi dV} = \frac{\alpha_1^2 H_{11} + \alpha_2^2 H_{22} + 2 \alpha_1 \alpha_2 H_{12}}{\alpha_1^2 + \alpha_2^2 + 2 \alpha_1 \alpha_2 S} \end{equation*}

(4.72)

with

\begin{equation*} S = \int \Phi_1^* \Phi_2 dV \qquad , \qquad H_{11} = \int \Phi_1^* h \Phi_1 dV = H_{22} \qquad \mbox{and} \qquad H_{12} = \int \Phi_1^* h \Phi_2 dV \qquad . \end{equation*}

(4.73)

Minimizing Eq. (4.72) for \(\alpha_i\) we get a system of linear equations

\begin{equation*} \begin{split} \alpha_1 (H_{11} - \epsilon') + \alpha_2 (H_{12} - \epsilon' S) & = 0\\ \alpha_2 (H_{12} - \epsilon' S) + \alpha_2 (H_{11} - \epsilon') & = 0 \end{split} \end{equation*}

(4.74)

This system has non trivial solutions only if the coefficient determinant vanishes, i.e.

\begin{equation*} (H_{11} - \epsilon')^2-(H_{12} - \epsilon' S)^2 =0 \end{equation*}

(4.75)

We find energy values

\begin{equation*} \epsilon_{\pm}' = \frac{H_{11} \pm H_{12}}{1\pm S} \label{e_bonding_antibonding} \end{equation*}

(4.76)

and Eigenvectors \(\alpha_1 = \alpha_2\) and \(\alpha_1 = -\alpha_2\), leading to

\begin{equation*} \psi_0= \frac{1}{\sqrt{2}} \left( \Phi_1 + \Phi_2 \right) \label{psi__0} \end{equation*}

(4.77)

and

\begin{equation*} \psi_1= \frac{1}{\sqrt{2}} \left( \Phi_1 - \Phi_2 \right) \label{psi__1} \end{equation*}

(4.78)

So according to Eq. (4.68) the complete symmetric wave function is calculated as

\begin{equation*} \psi_s(r_1, r_2) = \frac{1}{2} \left\{ \Phi_1(r_1)\Phi_2(r_2) + \Phi_2(r_1)\Phi_1(r_2) +\Phi_1(r_1)\Phi_1(r_2) + \Phi_2(r_1)\Phi_2(r_2) \right\} \label{psi_sym_2} \end{equation*}

(4.79)

and the antisymmetric one:

\begin{equation*} \psi_t(r_1, r_2) = \frac{1}{2} \left\{ \Phi_2(r_1)\Phi_1(r_2) - \Phi_1(r_1)\Phi_2(r_2) \label{psi_antisym_2} \right\} \end{equation*}

(4.80)

Eq. (4.79) is an excellent solution of the Schrödinger equation (4.64) for negligible Coulomb interaction.
Not taking into account the lattice periodicity and the large number of atoms in a solid we repeated the LCAO-calculation:

we determined the same matrix-elements
using atomic orbitals as components, we solved an Eigenvalue problem
the result is a linear combination of atomic orbitals.

We will check now, if the singlet state is as well a good approximation in the case of strong Coulomb interaction as it is included in the Schrödinger equation (4.62):

The first two terms in Eq. (4.79) describe a state where the electrons are located at different atoms. Even if the Coulomb interaction is strong, the effect will be small, since the additional Coulomb energy of these states to the complete energy is small (especially if the distance between both atoms is relatively large).
The last two terms describe a state of two electrons, located at the same atom. Independent of the distance of both atoms, the Coulomb energy will be large, leading to a strong increase of the energy of the singlet-state.
The last two terms describe a charged H\(^{-}\)-Ion and a proton. This is not a very precise picture of the physical state if the electron-electron-repulsion is important.
This problem does not occur in the triplet-state of Eq. (4.80); consequently the triplet-state (with magnetic moments) can be preferred in systems with a strong Coulomb-interaction.
The same effect we find in a solid of highly correlated electrons. In such systems the approach of separating the state into single-electron-states completely fails.

4.9.1 Mean-Field-Approximation for the description of the Coulomb-Coupling