2.3.2 Potentialtöpfe für Elektronen im Atom, Molekül und Festkörper

	Wir erweitern nun das Konzept des Potentialtopfes auf die Elektronen, die an einen Atomkern gebunden sind. Um ein Elektron aus dem Atom zu entfernen, müssen wir die entsprechende für das betreffende Elektron geltende Bindungsenergie aufbringen; sie ist für jeden Elektronenzustand definiert.
		Obwohl wir dasselbe Wort verwenden, hat die Elektronenbindungsenergie natürlich nichts mit der Bindungsenergie von Molekülen oder Festkörpern zu tun.
		Wir brauchen einen Abstand. Das ist zwar keine gut definierte Größe für die Elektronen, aber wir können einfach das Maximum der entsprechenden Wellenfunktion nehmen - für den Zweck der Visualisierung von Bindungen werden sowieso nur qualitative Verläufe gebraucht.
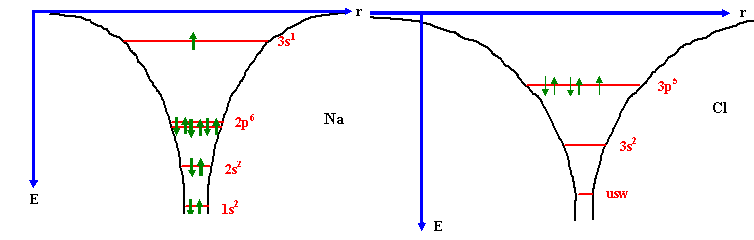
		Qualitiativ sieht ein Potentialtopf, z.B. für die Elektronen eines Na - oder Cl - Atoms dann so aus:

	Nochmal: Die Form der Töpfe und die Lage der Energieniveaus ist rein qualitativ. Was jedoch stimmt ist die Anzahl der Elektronen auf den Niveaus (wieder symbolisiert durch Pfeile) und die relativen Unterschiede in der Topfgröße und der Lage der obersten Niveaus.
		Die Niveaus liegen - im Gegensatz zu den Niveaus bei den Atomen - recht weiter auseinander wegen der geringen Masse der Elektronen. Sie sind natürlich nichts anderes als die Gesamtenergien, die aus der Lösung der Schrödingergleichung für das betrachtete Atom resultieren.
		Jedes Niveau trägt damit als "Namen" sein zugehöriges Triplett (ohne den Spin) der passenden Quantenzahlen. Das tiefste Niveau ist damit in jedem Potentialtopf immer das 1s1-Niveau.
	Analog zur Potentialtopfdarstellung der Atome, können wir die Elektronenniveaus als Energieniveau der "Schwingung" der Elektronen um den Kern betrachten. Es ist die Summe ihrer potentiellen und kinetischen Energie, die durch das E - Niveau gegeben wird.
	Die Ionisierungsenergie ergibt sich aus der Darstellung sofort als Abstand des obersten besetzten Niveaus von der Null-Linie.
		Der Nutzen einer derartigen Darstellung erschließt sich, wenn man jetzt die Potentialtöpfe für die Elektronen eines Moleküls betrachtet.
		Dazu bringen wir einfach die beiden individuellen Potentialtöpfe zusammen (im Bindungsabstand r0) und addieren die Kurven der potentiellen Energie. Im Beispiel des NaCl stellt sich dies so dar:

	Es ist anschaulich klar, daß das einzelne Elektron des Na seine Energie und damit auch die Systemenergie senken kann, indem es auf das zugängliche und energetisch tiefere Potential des Cl - Atoms übergeht. Damit entstehen zwei Ionen und die Ionenbindung wird wirksam.
		Die gemeinsamen Niveaus bräuchten natürlich im Prinzip eine neue Bezeichnung. Damit wollen wir uns aber hier nicht beschäftigen.
	Betrachten wir als nächstes die Metallbindung in dieser Darstellung. Wir nehmen als Beispiel wieder das Na.

	Wiederum sitzen die 3s - Niveaus außerhalb der Potentialtopfes des Atoms; das Niveau erstreckt sich jetzt durch den ganzen Kristall.
		Aber die dort vorhandenen Elektronen können ihre Energie nicht senken; es gibt keine tiefer gelegenen freien Niveaus.
		Das Pauli Prinzip verbietet, daß mehr als zwei Elektronen in einem Zustand sitzen - und das 3s - Niveau, obwohl es sich jetzt durch den ganzen Festkörper erstreckt, ist ein Niveau!
		Es muß etwas geschehen, damit alle Elektronen Platz finden. Die Lösung ist eine Aufspaltung der s - Niveaus. Es bilden sich ungeheuer viele (N = Zahl der beteiligten Atome) s - Niveaus aus, die energetisch zwar dicht beieinander liegen, aber im Sinne des Pauli Prinzips individuelle Zustände sind; ein sogenanntes Elektronenband. Das ist als ein farbliches Kontinuum dargestellt,; nur einige Niveaus sind als Linien markiert.
	Die Elektronen des Na besetzen die Hälfte der möglichen Zustände in dem s - Band; sie sind das "Elektronengas" der Metallbindung.
		Die Elektronen sind nicht mehr einzelnen Atomen zugeordnet; sie "laufen" frei durch das Metall
		Na ist damit (wie alle Metalle) ein elektrischer Leiter!
	Es ist wichtig, sich klarzumachen, dass das Bild oben und das alte Bild zur Metallbindung exakt dieselbe Sache zeigen - nur aus anderen Blickwinkeln und mit anderen Vereinfachungen und Schematisierungen.
	Wie sehen kovalente Bindungen aus. Betrachten wir den Si - Festkörper (einen Kristall) mit 4 gesättigten Bindungen in der sp3 - Hybridkonfiguration, erhalten wir schematisch folgendes Potentialtopfbild:

	Was die Graphik darstellt, ist der typische Fall eines Halbleiters. Allerdings ergibt sich das nicht direkt aus der Überlagerung der Einzelpotentiale, sondern es wird in diesen Bildern Wissen illustriert, das man aus tiefergehenden Betrachtungen gewonnen hat. Was wirklich passiert bei der Bindung läßt sich nicht direkt graphisch, wie hier insinuiert, erschließen.
	Die sp3 - Zustände sind mit 4 Elektronen besetzt und hätten Platz für 8. Wiederum überlappen sich die Zustände benachbarter Atome und spalten dabei in N Zustände auf mit N = Zahl der beteiligten Atome.
		Aber das gebildete Band ist zweigeteilt. Ein Teilband (es heißt Valenzband) liegt gerade noch im Potentialtopf eines Atoms; es ist voll besetzt mit den 4 Elektronen pro Atom. Da unsere Potentialtopfdarstellung scharfe Grenzen vorgibt obwohl keine da sind, ist das Band gestrichelt durch die Potentialschwelle gezeichnet.
		Das zweite Teilband ist vom ersten durch eine Energielücke getrennt. Es ist vollständig leer und heißt Leitungsband.
		Der Name ist klar: Würde das Leitungsband Elektronen enthalten, wären sie frei beweglich; Si wäre ein elektrischer Leiter.
	Wir spüren: Der Trick der gesamten Halbleitertechnik liegt darin, wie man Elektronen in das Leitungsband bekommt - aber das betrachten wir später.

© H. Föll (MaWi 1 Skript)