Hardness

All people, without exception, have a pretty good idea of what "hardness" means in the context of materials properties. Extremely few people, however, have a decent notion of what the terms "yield stress" or "maximum elongation" tells us about materials properties.
Ironically, while the two latter properties are well-defined, hardness is not!
Yield stress, as we know, can be measured in precisely defined ways, and can be expressed in terms of basic material properties.
Hardness is different. It is not uniquely defined, and that means there is no unambitious way of measuring it. There are only some recipes - that's why we have several hardness scales in parallel.
Essentially, there are two types of basic hardness measurement set-ups (plus some more unusual principles).
1. Measure the size of an indentation made by some indenter under a known load. The following hardness tests use this principle:
2. Measure the depth to which an indenter penetrates under specified conditions. The following hardness tests use this principle:
More unusual or outdated are
  • Mohs hardness scale (the first one), defined via "what scratches what".
  • Shore scleroscope principle: measure the rebound of a ball or hammer.
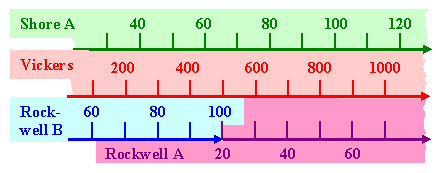
In the "Materials in Action" series, "Structural Materials", page 100, the scales are compared (which is not easy).
Here we usually use the Vickers scale. It runs from 0 to about 3000; the unit is essentially that of stress (Pa); but the numbers are given in outdated units:
In the "Materials in Action" series you will find an unusual unit: "kgf", which is kilogram-force, which is something different from a "kg", because that was and is a mass. Nevertheless, the unit for the hardness is kg/mm2; what is meant is the force that a mass of one kg experiences in the gravitational field of the earth. In German the unit "kilopond" (kp) was used; it's the same thing. Of course we have 1kg/mm2 » 10N/10–6 m2 = 10–5 Pa
Here is a table with some Vickers hardness data:
Material Vickers hardness Material Vickers hardness Material Vickers hardness
Sn 5 Limestone 250 Polypropylene 7
Al 25 MgO 500 Polycarbonate 14
Au 35 Window glas 550 PVC 16
Cu 40 granite 850 Epoxy 45
Fe 80 quartz 1200
 
Mild steel 140 Al2O3 2500    
Hardened steel 900 WC 2500    
Hardness measures in some lumped way a combination of elastic, plastic, and fracture properties, i.e. it combines somehow Yield stress, Youngs modulus and fracture parameters.
There is, however, no unique formula giving the hardness number as a function of the primary parameters.
The best one can do is to provide some approximate relations for certain classes of materials.
For relatively soft metals and for steel, respectively, there is a very simple relation between the Vickers Hardness HV and the yield stress RP or the tensile strength RM
HV    »     3    RP "soft" metals
3.2 RM steel
Of course, you have to express the strength parameters in kg/mm2, too
This makes life easier and explains why we have not much dealt with hardness here: For our materials of interest, it is essentially the same as the much better defined parameters governing plastic deformation.
Life would be even more easier, if most scientists would use the same hardness scale. Of course, they don't, so here is an approximate conversion, adopted form the "Materials in Action " Series already mentioned.
Hardness conversion

Mit Frame Mit Frame as PDF

gehe zu 4.1.4 Versetzungen und plastische Verfomung

gehe zu 8.4.1 Plain Carbon Steels

gehe zu Edelsteine

gehe zu 8.1.1 Plastische Verformung von Kristallen

gehe zu Elastizitätsmodul in Zahlen

gehe zu Elementare Maßeinheiten

© H. Föll (MaWi 1 Skript)