Frank- und Shockley Versetzungen

Die Graphik zeigt in der <110> Projektion des fcc Gitters einen intrinsischen Stapelfehler, berandet durch eine Shockley Partialversetzung (linkes Bild) oder eine Frank Partialversetzung (rechtes Bild).

Auch wenn der Versetzungscharakter der Shockley - Partialversetzung nicht so offenkundig ist wie beim Frankschen Gegenstück, muß man nur immer die Voltaterra Definition bedenken, um den Versetzungscharakter zu sehen und auch den Burgersvektor ableiten zu können.

	Schneiden wir entlang der {111} Ebene, entspricht das einem Schnitt in der Stapelfolge ABCABCABC... , z.B zwischen A und B. Wir können nun einen Staperfehler inkl. berandende Versetzung auf 2 Weisen erzeugen:
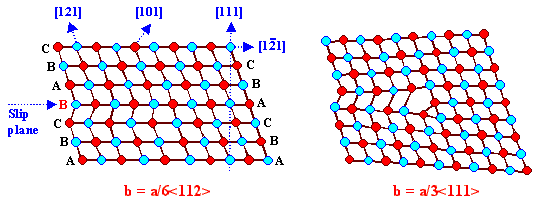
		Wir können das Gitter um eine Ebenendicke aufweiten und eine Lage Atome einfügen (das wäre dann die C - Lage) oder eine Ebene herausnehmen. In jedem Fall müssen wir senkrecht zum Schnitt die Ebenen um a/3<111> senkrecht zur Schnittebenen bewegen und schaffen damit einen Franksche Partialversetzung.
		Wir können aber auch z. B. die B - Ebene durch eine Verschiebung in der Ebene in die C - Lage überführen. Dann muß kein Material eingefüllt oder entnommen werden. Die Verschiebung kann durch drei Vektoren erfolgen, die alle von der B - Position zu einer der drei benachbarten C - Positionen zeigen. Die Verschiebungsvektoren, die gleichzeitig wieder die Burgersvektoren der berandenden Partialversetzungen sind, haben alle den allg. Vektor a/6<112>.
	Falls Sie die Aufgabe 3-7 gemacht haben, wird Ihnen das alles bekannt vorkommen!

Mit Frame

4.2.1 Allgemeines

Übung 3.3-3