Stirlings Formula

Stirlings formula is an indispensable tool for all combinatorial and statistical problems because it allows to deal with factorials, i.e. expressions based on the definition 1 · 2 · 3 · 4 · 5 · .... · N := N!

It exists in several modifications; all of which are approximations with different degrees of precision. It is relatively easy to deduce its more simple version. We have

ln x!	=	ln 1 + ln 2 + ln 3 + .... + ln x	=	x S 1	ln y

With y = positive integer running from 1 to x

For large y we may replace the sum by an integration in a good approximation and obtain

x S 1	ln y	»	x ó õ 1	(ln y) · dy

With 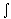(ln y) · dy = y · ln y – y, we obtain

ln x!	»	x · ln x – x + 1

This is the simple version of Stirlings formula. it can be even more simplified for large x because then x + 1 << x · ln x; and the most simple version, perfectly sufficient for many cases, results:

ln x!	»	x · ln x

However!! We not only produced a simple approximation for x!, but turned a discrete function having values for integers only, into a continuous function, giving numbers for something like 3,141! - which may or may not make sense.

This may have dire consequences. Using the Strirling formula you may, e.g., move from absolute probabilities (always a number between 0 and 1) to probability densities (any positive number) without being aware of it.

Finally, an even better approximation exists (the prove of which would take some 20 pages) and which is already rather good for small values of x, say x > 10:

x!	»	(2p)^1/2 · x^{(x + ½)} · e^{– x}

With frame

2.1.1 Simple Vacancies and Interstitials

Solution to Basic Exercise 2.1-4