|
Unter Kriechprozessen (engl. "creep processes")
verstehen wir die langsame plastische Verformung eines Materials unter einer konstanten
angelegten Last; diese Definition gilt für alle Materialien. |
|
 |
Mit Versetzungskriechen können damit nur Kriechprozesse
in kristallinen Materialien gemeint sein - in amorphen Materialien gibt es keine Versetzungen.
Was aber nicht bedeutet, dass es kein Kriechen gäbe! |
|
 |
Im folgenden wollen wir auch nur Versetzungskriechen behandeln,
denn es ist ein vergleichsweise gut verstandener Prozeß. |
 |
Versetzungskriechen hat uns alle schon mal
geärgert: es ist zum Beispiel die Ursache dafür, daß Schrauben im Laufe der Zeit manchmal locker werden
ohne daß die Mutter sich gedreht hat. Dasselbe gilt für die Fahrradkette,
die im Gebrauch allmählich etwas länger wird und dann nicht mehr gut läuft. |
|
 |
Die Schraube mit angezogener Mutter steht unter konstanter Zugspannung;
wenn sie "kriecht" wird sie l a n g s a m länger, damit verringert sich die Spannung
- die Schraube ist locker. |
|
 |
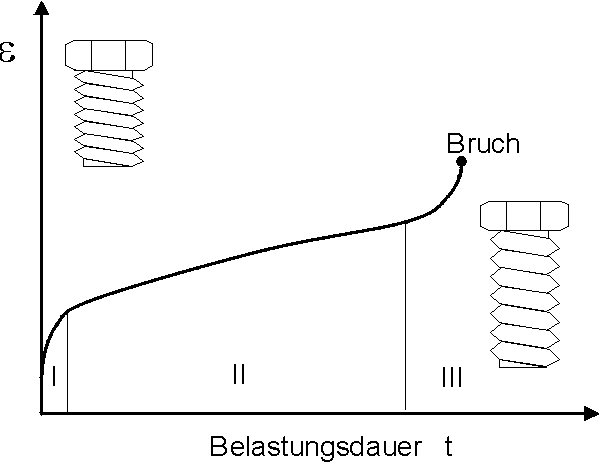
In einem Dehnungs - Zeit Diagramm sieht das typischerweise
so aus: |
| |
|
| |
 |
Gezeigt ist hier die Dehnung bei konstanter
Last; früher oder später wird das zum Bruch führen. Diese Diagramm entspricht aber nicht
dem Beipiel der Schraube, bei dem die Last nicht konstant ist sondern sinkt und der Kriechprozeß - sofern nicht jemand
die Schraube wieder anzieht - zum Stillstand kommt. |
 |
Zunerst, im Bereich I, dehnt sich das Material noch relativ schnell, dann
über einen längeren Zeitraum - der viele Jahre betragen kann - im Bereich II nur noch langsam, zum Schluß
folgt auf eine schnellere Dehnungsgeschwindigkeit im Bereich III der Bruch. |
|  |
Und das bei einer während der ganzen Zeit konstanten Spannung,
die im üblichen Spannungs - Dehnungs Diagramm zu einer konstanten
Dehnung führen sollte. |
|
 |
Wir müssen uns klar machen, daß hier etwas neues geschieht,
das in der bisherigen Behandlung der plastischen Verformung nicht vorkommt. |
 |
Bisher haben wir verstanden, daß nach überschreiten der Fließgrenze Rp
Versetzungen solange erzeugt und bewegt werden, bis die entsprechende Dehnung sich eingestellt hat. Dies ist ein schneller Prozeß, der auf einer Zeitskala im Sekundenbereich abläuft. Wird die Fließgrenze
nicht erreicht, wird Versetzungsbewegung nicht stattfinden; alle Versetzungen sind an irgendwelchen Hindernissen verankert. |
|
 |
Liegt die für das betreffende Material typische Dehnung vor, ist immer ein Gleichgewichtszustand erreicht
zwischen den Kräften die Versetzungen bewegen wollen - verursacht durch die äußere Spannung - und den Verankerungskräften
an anderen Defekten. |
|
 |
Offensichtlich aber bedingt der Kriechprozeß, daß Versetzungen weiterlaufen, wenn auch
l a n g s a m. Es muß also einen langsamen Mechanismus geben, der es Versetzungen erlaubt sich von Hindernissen zu
lösen. |
 |
Dieser Mechanismus, der insbesondere Versetzungsbewegung außerhalb der
Gleitebene ermöglicht, hat sein Ursache in der Wechselwirkung
von Versetzungen (und auch Korngrenzen) mit diffundierenden Leerstellen und heißt
Versetzungsklettern. Wir betrachten ein einfaches Beispiel dazu: |
|
 |
Eine Stufenversetzung sei an (kugelförmigen) Ausscheidungen verankert. Unter der auf sie wirkenden
Kraft baucht sie sich zwar aus, kann jedoch nicht weiterlaufen. Dies sieht etwas so aus: |
| |
|
 |
Betrachen wir die Verankerung der Versetzung an einer der Ausscheidungen im
Querschnitt, sieht dies etwa so aus |
| |
|
 |
Wir fragen uns natürlich, woher die Leerstellen kommen und warum sie ausgerechnet
zu den "richtigen" Stellen der steckengebliebenen Versetzung wandern. |
|
 |
Leerstellen wandern besonders gerne in Gebiete, die unter kompressiver
Spannung stehen. Anschaulich gesagt, ist dort die Dichte zu hoch, sie kann durch den Einbau von Leerstellen erniedrigt werden.
Ein solches Gebiet ist nun genau der Kern unserer steckengebliebenen Stufenversetzung, sie zieht Leerstellen förmlich
an. |
|
 |
Als Quelle der Leerstellen wirken andere Versetzungen. Um das zu verstehen, drehen wir gedanklich den Absorptionsprozeß
um: Eine Versetzung kann genausogut eine Leerstelle emittieren wie absorbieren. Dazu muß sich einfach ein Atom einer
Nachbarebene an die eingeschobene Halbebene anlagern; auf der Nachbarebene sitzt dann eine Leerstelle die durch das Gitter
weggdiffundieren kann. |
|
 |
Letzlich können die Leerstellen, die im thermodynamischen Gleichgewicht vorhanden sein müssen,
nur an Defekten entstehen; ein Atom im perfekten Kristall kann ja nicht einfach verschwinden. |
 |
Ganz allgemein Betrachtet, herrscht an einer Versetzungslinie immer ein Gleichgewicht
zwischen Emission und Absorption von Leerstellen, so daß die Gesamtkonzentration gerade der Gleichgewichtskonzentration
entspricht. |
|
 |
Ohne äußere Kräfte sind beide Prozesse ausgeglichen. Mit äußeren Kräften,
die den den gestörten Bindungen im Versetzungskern ein gerichtetes Dehnungsfeld überlagern, ändert sich das
Bild, wir erhalten den sogenannten Peach-Koehler-Prozeß. |
|
 |
Je nach Lage der Versetzung im äußeren Dehnungsfeld wird sie zum Netto Exporteur oder Importeur
von Leerstellen. Der Nettofluß an Leerstellen, der ja immer mit einem entgegengesetzt gleich großen Fluß
an Materie verbunden sein muß, erfolgt dabei so, daß die Probe sich in Richtung der äußeren Kraft
dehnt. Stark schematisiert sieht das so aus: |
|
|
|
|
 |
Von den blauen Stufenversetzungen, die zur gewünschten Scherverformung unter den wirkenden Kräften
nichts beitragen können, fließt ein Nettostrom am Lerrstellen zu den roten Versetzungen, die dann klettern und
durch nachfolgende Bewegung bis zum nächsten Hindernis den Körper im Laufe der Zeit abscheren werden. |
 |
Ohne in Details zu gehen, ist die fundamentale Abhängigkeit des Versetzungskriechens
von Materialparametern und der Temperatur leicht zu formulieren: |
|
 |
Der Prozeß ist abhängig von der Zahl oder besser
Konzentration der Leerstellen und ihrer Beweglichkeit, d.h. von der Bildungs- und Wanderungsenthalpie.
Er ist thermisch aktiviert, damit erwarten wir einen Boltzmannfaktor
wie bei der Selbstdiffusion, d.h. den Term
exp –(EF + EM)/kT . |
|
 |
Da als treibende Kraft die anliegende Spannung auftritt, erwarten wir eine Proportionalität zur Spannung
s, in der einfachsten Form als ein Potenzgesetz (sn,
wobei n zunächst unbestimmt bleibt). |
|
 |
Weiterhin muß sich die Art und das Gefüge des spezifischen Materials auswirken - ein gegebenes
Material mit viel Versetzungen und kleinen Ausscheidungen als Hindernisse wird anders kriechen als ein identisches Material
mit wenig Versetzungen und großen Ausscheidungen - das kann man in einem Vorfaktor A berücksichtigen.
|
 |
Damit erhalten wir die "Kriechformel" für
den Bereich II des Versetzungskriechen: |
| |
de
dt |
= |
A · sn · exp – |
EF + EM
kT |
|
|
 |
Da die relevanten Parameter experimentell bestimmbar sind, kann man damit arbeiten,
d.h. die Lebensdauer von Materialien unter Belastung ausrechnen. |
 |
Am Rande sei erwähnt, daß Klettern von Versetzungen nicht nur zu mechanischen
Problemen führen kann, sondern auch zu elektrischen. |
|
 |
In Laserdioden bewirkt zum Beispiel das
Versetzungsklettern von den im Material (z.B. GaAs) noch vorhandenen wenigen Versetzungen im Betrieb des Lasers,
daß der Wirkungsgrad allmählich zurückgeht. Der Laser altert und wird irgendwann nicht mehr funktionieren. |
|
 |
Die Notwendigkeit, dieses "Irgendwann" aus dem Bereich von wenigen Minuten in den
Bereich vieler Jahre zu verschieben, war eine der Hauptaktivitäten der Materialwissenschaftler für einige Jahre
vor der Masseneinführung der Laserdioden, die heute jeder in seinen CD-Laufwerken und anderswo problemlos benutzt. |
 |
Viel genauer soll Versetzugskriechen an dieser Stelle nicht behandelt werden,
wer mehr wissen möchte muss schon recht tief einsteigen. |
| | |
© H. Föll (MaWi 1 Skript)