6.2 Atomare Betrachtung der Diffusion

6.2.1 Sprungraten, Leerstellen- und Zwischengitteratomwanderung

Sprungraten

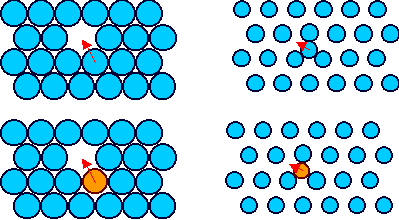
	Im Grunde ist im vorhergehenden Unterkapitel die Diffusion von Atomen bereits behandelt. Der Elementarprozeß ist (fast) immer der Sprung eines Atoms in eine Leerstelle oder der Sprung eines Zwischengitteratoms auf einen Nachbarplatz im Zwischengitter. Dabei gibt es in einatomigen Kristallen vier fundamentale Möglichkeiten, sie sind in der Graphik dargestellt
		1. Ein Atom des Kristalls springt in eine Leerstelle (links oben).
		2. Ein substitutionelles Fremdatom, springt in eine Leerstelle (links unten).
		3. Ein Eigenzwischengitteratom springt auf einen Nachbarplatz (rechts oben)
		4. Ein interstitielles Fremdatom springt auf einen Nachbarplatz (rechts unten)
		Es gibt noch einige exotische Möglichkeiten (z.B. ein interstitielles Fremdatom springt auf einen Gitterplatz und wirft das bisher dort sitzende Kristallatom auf einen Zwischengitterplatz), sie spielen aber kaum eine Rolle (außer im Si) und sollen nicht weiter behandelt werden.
	In jedem Fall ist eine für den betrachteten Sprung spezifische freie Enthalpiebarriere zu überwinden. Betrachten wir zunächst die Zwischengitteratomdiffusion (Index "i") genauer:
		Die Sprungrate r i ist gegeben durch Anlauffrequenz mal Boltzmannfaktor, d.h.
		ri = n · exp –  GM,i kT
		Wobei der Index (M,i) für "Migration " des "interstitials" steht, d.h. für die Diffusion des Zwischengitteratoms).Wir machen die in einem fortgeschrittenen Modul im Detail ausgeführten, aber eigentlich klaren Näherungen:
		GM,i  =  HM,i  –  TSM,i  »  EM,i  –  TSM,i
		Mit SM,i = Entropie eines Sprungs = Wanderungsentropie » 1 k (k = Boltzmannkonstante).
		Dass wir auch eine Wanderungsentropie haben ist qualitativ klar: Man muß für einen Sprung nicht nur Energie zuführen, sondern der Kristall ist im Momemt des Sprungs auch ein bißchen unordentlicher, man braucht also auch Entropie. Das schlägt sich aber nur ein bißchen im Vorfaktor zum Exponentialterm nieder, ist also nicht besonders wichtig.
	Eingesetzt erhalten wir
		ri = n · exp   S k   · exp –  EM,i kT
		Das ist die Zahl der Sprünge, die ein Zwischengitteratom pro Sekunde durchführt und damit auch die mittlerer Sprungrate aller anderen ZGA, denn was ein ZGA macht, machen alle.
	Der Vorfaktor ist eine Art Materialkonstante, wir bezeichnen ihn vorläufig mit D0 (als Abkürzung für Diffusion ); d.h.
		D0 = n · exp  S k
		Die Energie EM,i heißt Wanderungsenergie der (jeweils betrachteten) Zwischengitteratome, Aktivierungsenergie der Zwischengitteratom-Diffusion oder Diffusionsenergie der ZGA.
		Typische Werte von ZGA - Wanderungsenergien liegen im Bereich 1 eV oder kleiner.Wir können Wanderungsenergien als Materialkonstanten auffassen; denn für jedes passende Paar (A,B) von Atomen mit A = Atom des Gitters und B = diffundierendes Zwischengitteratom existiert eine Wanderungsenergie; Beispiele finden sich weiter unten.

	Leerstellenwanderung
	Wie groß sind die Sprungraten von Atomen, die über einen Leerstellenmechanismus wandern?
		Im Gegensatz zur ZGA Diffusion kann nur der Bruchteil der Atome überhaupt springen, der eine Leerstelle als Nachbar hat; alle andern haben eine Sprungrate r = 0.
		Die mittlere Sprungrate eines beliebigen Atoms ist damit gegeben durch die Wahrscheinlichkeit , daß bei einem Anlauf genügend Energie vorhanden ist (= D0 · exp – (EM/kT)) mal der Wahrscheinlichkeit, daß gerade ein Nachbarplatz mit einer Leerstelle "besetzt" ist (» exp – (EF,V/kT). Insgesamt erhalten wir für die Sprungrate der substitutionell diffundierenden Atome:
		rsub. Atome  = D0 · exp  –  EM kT    · exp –  EF,V kT
	EM ist dabei die Aktivierungsenergie für den Sprung der betrachteten Atomsorte in eine benachbarte Leerstelle; in D0 stecken wieder die Anlauffrequenz und (kleine!) Entropieterme.
		Das betrachtete Atom kann ein Fremdatom, aber insbesondere auch ein reguläres Atom des Kristallgitters sein; in diesem Fall reden wir über die Selbstdiffusion in einem Kristall.
		Der Sprung eines Gitteratoms in eine Leerstelle ist aber gleichbedeutend mit dem Sprung einer Leerstelle in die entgegengesetzte Richtung, man kann genausogut von EM,V  reden, der Wanderungsenergie einer Leerstelle. Damit erhalten wir für die Sprungraten aller Atome eines Kristalls im Falle der Selbstdiffusion , rSD,
		rSD  =  D0,SD · exp –  EM,V kT   · exp –  EF,V kT             =  D0,SD · exp –  EM,V + EF,V kT

	Entscheidend für die Selbstdiffusion ist also die Summe der Aktivierungsenergien für die Erzeugung und Wanderung der Leerstelle.
		Die Gesamtzahl der Sprünge (= R) die von den N0 Atomen des Kristalls pro Sekunde durchgeführt werden, ist also
		R  =  N0 · rSD
	Für die Diffusion substitutioneller Fremdatome lassen sich die Beziehungen direkt übernehmen. Statt der Wanderungsenergie der Leerstellen verwenden wir die jeweilige Wanderungsenergie des Fremdatoms, statt der Gesamtzahl der Gitteratome die Gesamtzahl der Fremdatome, NFA oder ihre Konzentration cFA = NFA/N0.

	Wie groß sind typische Wanderungsenergien? Als grobe Faustregel kann man ca. 0,5 eV für dieZwischengitteratome nehmen und 1 eV für Sprünge der Leerstelle.
		Einige typische Werte sind in den Tabellen weiter unten angegeben
		Damit wird meistens die Diffusion von Zwischengitteratomen, auch direkte Diffusion genannt, sehr viel schneller sein als die Diffusion von Atomen mit Hilfe von Leerstellen.
		Dazu wollen wir eine Übung machen, im Link finden sich die notwendigen Zahlenwerte.
		Übung 6.2-1 Einige Zahlen zur Diffusion von Atomen
	Anschaulichere Darstellungen der Diffusion von Atomen findet man in Arrheniusdarstellungen, die dann die Arrheniuskurven für mehrere Atome in einem Diagramm enthalten können. Im Link findet sich ein Beispiele zum Silizium
		Arrheniusdarstellung der Diffusion zahlreicher Atome in Silizium.
		Eine ganz andere, für sich selbst sprechende Darstellung findet sich in diesem Link.
	Eine Frage drängt sich auf: Wie misst man eigentlich Diffusionskoeffizienten, Wanderungs- und Bildungsenthalpien von atomaren Fehlstellen usw.?
		Mit Mühe, viel Geld und sehr viel Wissen! Bevor das aber behandelt werden kann, müssen wir uns erst die nächsten Unterkapitel reinziehen.

	Diffusionsstrom
	Was wir bisher behandelt haben, ist ein fröhliches Herumgehüpfe von Atomen und atomaren Defekten, alle Richtungen sind gleichberechtigt.
		Im Mittel werden genausoviel Atome nach links wie nach rechts gesprungen sein; im Mittel hat sich nichts geändert.
		Das muß auch so sein, denn wir haben thermodynamisches Gleichgewicht unterstellt. Die Konzentration der Leerstellen ist die Gleichgewichtskonzentrationen, die Konzentration aller Teilchen ist überall (im Mittel) gleich groß.
	Was geschieht aber, wenn wir ein Experiment machen, bei dem die Konzentration an Fremdatomen zu Beginn nicht überall gleich groß war? Denken wir an die alten Schmiede, die irgendwie Kohlenstoff (oder Stickstoff) von außen in des Eisen des Schwertes einbringen, d. h. eindiffundieren mußten. Oder an die modernen Mikroelektroniker, die eine exakt bestimmte Konzentration an P oder B in fest vorgegebene Bereiche des Siliziums einer integrierten Schaltung einbringen müssen.
		Letztlich werden diese gezielt eingebrachten Atome mit einem der beschriebenen Mechanismen ins Innere des Materials eindiffundieren; ihre Konzentration wird sich systematisch und stetig ändern. Wir haben kein Gleichgewicht mehr, denn wir haben eine zeitliche Änderung einer Teilchenzahl.
		Die zugehörige mathematisch-phänomenologische Beschreibung ist älter als das Verständnis der atomaren Vorgänge.Wir werden sie im nächsten Unterkapitel behandeln.

© H. Föll (MaWi 1 Skript)