6.1.3 Merkpunkte zu Kapitel 6.1: Reaktionsraten

Kinetik bedeutet hier: Lehre vom Weg ins Gleichgewicht durch Bewegung (von Atomen) mit "Nettoeffekt" und "Bewegung" im TD GG ohne "Nettoeffekt"
Leerstellen Diffusion Diffusionsprung
Weg Nichtgleichgewicht Þ Gleichgewicht: Es muss sich netto "was" ändern!
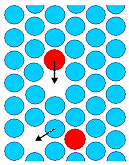
Bei Festkörpern / Kristallen: Atome müssen diffundieren
Zu betrachtender Elementarprozess: "Sprung" eines Teilchens (=Atom).
Atome "springen" aber auch im Gleichgewicht! Was zählt ist nur der Nettoeffekt (im Gleichgewicht=0)
Analogie: Girokonto. Kein Nettoeffekt falls Zufluß=Abfluß
 
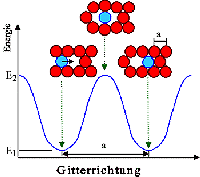
Sprünge erfolgen immer über Energiebarrieren (besser: Enthalpiebarrieren).  
r  =  n · p(DE)
n=Anlauffrequenz;
p(DE) Wahrscheinlichkeit zur
Überwindung der Energiebarriere DE
Ansatz für Sprungrate r=Zahl Sprünge eines Teilchens pro Sekunde:  
 
Für p(DE) gilt immerder Boltzmannfaktor:
p(DE)  =  exp –   DE
kT
Extrem wichtige Gleichung; wird sehr häufiig auftauchen!
p(DE) für Atome in einem Kristall ist die Wahrscheinlichkeit dafür, dass in den Vibrationen um die Ruhelage (mit "statistischen" Amplituden) die Energie DE steckt.  
 
Damit Gesamtsprungrate R von N Teilchen über Barriere E.
R  =  N · r  =  A · exp – E
kT
Vorfaktor A enthält die Anlauffrequenz n und evtl. noch andere ("unwichtige") Faktoren
   
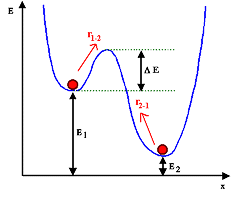
Gleichgewicht zwischen zwei E-Niveaus 1 und 2 bedingt
R1-2=R2-1
Gleichgewicht über Energiebarrieren
N1
N2		 =exp – E1 – E2
kT 
Damit Zentralformel für die "Besetzung" von E-Niveaus im TD GG
Entscheidend ist nur E1 – E2; DE bestimmt nur, wie lange es dauert, bis GG eingestellt ist.  
 
Verallgemeinert und mit leichter Näherung (Ni << N0) erhält man eine Zentralformel der Materialwissenschaft:
Ni  =  N 0 · exp – Ei
kT 
Verteilung klassischer Teilchen im TD GG auf gegebene Energieniveaus Ei mit Grundniveau E0=0 eV für alle Systeme.
Diese Art der Verteilung von Teilchen auf verschiedene E-Niveaus heißt Boltzmannverteilung oder Boltzmannstatistik.  
Bedeutung Boltzmannstatistik: Nie mehr Abzählen und Kombinatorik für Entropieteil der freien Energie / Enthalpie!.  
     
Anwendung auf atomare Fehlstellen (AF) im TD GG:  
NAF  = N0 · exp –  EF
kT 
Teilchen (i.d.R.=Atome) habe zwei E-Niveaus: Grundniveau E0 auf Gitterplatz, und "angeregtes" Niveau EF (=Bildungsenergie) bei Bildung einer AF  
Mit Frame Zurueck Weiter als PDF

© H. Föll (MaWi 1 Skript)