6.1.2 Energiebarrieren und ihre Überwindung

Energiebarrieren und Sprungwahrscheinlichkeit

	Betrachten wir, anknüpfend an die vorausgegangene Erörterung, jetzt die Situation eines Teilchens in einem Kristall, das aber zu einem System vieler Teilchen gehört.
		Alle Teilchen sind identisch, was eines macht, machen auch alle anderen. Im Mittel natürlich, immer nur im Mittel.
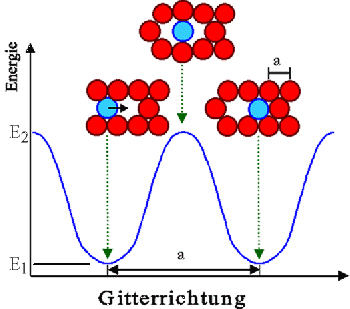
	Die folgende Graphik zeigt den Verlauf der Energie (genauer: Enthalpie) für dasjenige Atom, dessen Sprung in die Leerstelle wir betrachten; in der Graphik ist es blau markiert.
		Das jeweilige Energieminimum entspricht dem Gleichgewichtsplatz im Gitter; das Maximum der Energiebarriere korrespondiert mit der gezeigten Konfiguration, in dem das springende Atom eine energetische Sattelpunktslage hat (in zwei Richtungen geht es energetisch bergab; in die dazu senkrechten Richtungen bergauf, topologisch entspricht das einem Sattel)
		Für irgendein anderes Atom, das eine Leerstelle als Nachbar hat, sieht die Lage exakt identisch aus. Alle Nachbaratome zu irgendeiner Leerstelle sitzen energetisch im Niveau E1.
	Wie lange wird man im Mittel warten müssen, bis das Bezugsatom in die Leerstelle hüpft? Nennen wir diese mittlere Zeit t, dann können wir eine mittlere Sprungfrequenz oder Sprungrate r = 1/t definieren, die angibt, wie oft die Leerstelle pro Sekunde einen Sprung durchführt.
		Denn für die Sprünge der Leerstelle ist es gleichgültig, welches der Nachbaratome springt. Wenn eines davon (im Mittel) 0,1 Sekunden braucht, werden jedenfalls (im Mittel) 10 Atome pro Sekunde in die Leerstelle springen - und damit macht die Leerstelle (im Mittel) 10 Sprünge.
		Wir können die Sprungrate und das Energiediagramm deshalb auch auf die Leerstellen beziehen und sagen die Leerstelle "hüpft" über die Energiebarriere. Das ist letztlich einfacher, da wir dann die Bewegung einer Leerstelle verfolgen, statt das Gehüpfe vieler Atome.
	Wie groß ist die (mittlere) Sprungrate r der Leerstelle? Und zukünftig werden wir uns das "im Mittel" ersparen, wir wissen, was gemeint ist!
		Wenn alle Atome auf ihren Gitterplätzen stillsitzen, wird r = 0 sein müssen. Das passiert aber nur bei T » 0K; denn bei endlichen Temperaturen sitzen die Atome ja nicht still, sondern schwingen in ihrem Potentialtopf um ihre Gleichgewichtslage. Ihre mittlere Energie ist ja gerade ein Maß für die Temperatur, es gilt
		E  =  1 2   · f · kT
	Die Energie eines Atoms (oder der Leerstelle) fluktuiert aber um den Mittelwert herum- mal ist sie größer, mal kleiner.
		Gelegentlich kann damit vorkommen, dass ein Atom soviel Energie zur Verfügung haben wird, daß es die Energiebarriere überwinden kann.
		Mit zunehmender Temperatur und damit mittlerer Energie, steigt erkennbar die Wahrscheinlichkeit, daß ein Sprung durchgeführt wird. (Mit zunehmendem mittlerem Einkommen vieler steigt die Wahrscheinlichkeit, dass mal einer eine Million hat).
	Im Potentialbild ließ sich das leicht illustrieren. Das Atom schwingt um die Ruhelage, d. h. es läuft mit seiner Schwingungsfrequenz n gegen die Energiebarriere an. Je nach momentaner Energie in der Schwingung (mit dem Mittelwert 3/2 kT), kommt es mehr oder weniger weit hoch.
		Wenn es dabei zufällig mal eine Energie ³ DE hat, wird es einen Sprung durchführen.
		Damit können wir für die Sprungrate r  folgende ganz allgemeine Beziehung aufschreiben:
		Sprungrate r  =  Zahl der Anläufe n · Wahrscheinlichkeit p(DE) für E ³ DE oder r   =   n · p(DE)
		Mit n = mittlere Schwingungsfrequenz der Atome, p(DE) = Wahrscheinlichkeit für E ³ DE.

	Die Schwingungsfrequenz n ist uns im Prinzip bekannt, sie kann für ein bekanntes Bindungspotential errechnet werden. Als Faustregel kann (oder besser muß) man sich merken
		n  »  1013 Hz
		Was noch fehlt, ist die Wahrscheinlichkeit p = p(DE) für das Vorhandensein der richtigen Energie.
	Die richtige Formel für p(DE) stammt wie schon die Entropieformel von Ludwig Boltzmann. Wir leiten sie nicht her, sondern postulieren einfach:
		p(DE)  =  exp –   DE kT
	Die Sprungrate r eines Teilchens wird damit
		r  =  n · exp –   EM kT
		Dabei haben wir für die Energiebarrierenhöhe DE gleich den gebräuchlichen Ausdruck EM = Wanderungs- oder Migrationsenergie verwendet. Der Index "V" taucht nicht mehr auf, denn offensichtlich gilt die Betrachtung nicht nur für Leerstellen, sonder auch für Zwischengitteratome oder alles was sonst noch in atomaren Dimensionen "statistisch" herumhüpft.

	Alle Prozesse, die dieser Formel gehorchen, nennen wir "thermisch aktivierte Prozesse"
		Das Grundprinzip ist immer dasselbe: Vorhandene fluktuierende thermische Energie kann mit einer bestimmten, durch die Formel gegebenen Wahrscheinlichkeit, einen bestimmten Wert zu einer bestimmten Zeit an einem bestimmten Ort annehmen.
		Dadurch kann mit einer bestimmten Wahrscheinlichkeit ein bestimmter Prozeß aktiviert werden.
		Liest sich bestimmt blöd, aber die Formel ist derart allgemein, dass man sie halt nur in allgemein gehaltener Sprache beschreiben kann.

	Boltzmannverteilung
	Diese Formel kommt uns bekannt vor; sie war der wesentliche Term bei der Konzentration von Leerstellen im thermischen Gleichgewicht mit DE = HF(V) = Bildungsenthalpie der Leerstelle. (Wir werden gleich sehen warum).
		Wir postulieren diese Formel hier ohne weitere Begründung, sie läßt sich nur im Rahmen der statistischen Thermodynamik sauber herleiten. Im Hyperskript "Einführung in die Materialwissenschaft II" werden wir aber auf die Herleitung noch etwas näher eingehen.
	Wir können jetzt sofort einige Verallgemeinerungen vornehmen und weitreichende Folgerungen ableiten.
		Dazu schauen wir uns den Fall an, dass die Energieminima links und rechts der Barriere verschieden tief sind. Das sieht dann etwa so aus:
	Die Teilchen werden im Beipiel oben mit einer bestimmten Rate über die Energiebarriere springen, wir verallgemeinern das jetzt ein wenig zu der Sprungrate R für eine gegebene Zahl N an Teilchen und erhalten die Gleichung
		R  =  N · r  =  A · exp – E kT
		R sagt uns also, wieviel Teilchen aus den N vorliegenden pro Sekunde über die Energiebarriere hüpfen.
		Der Vorfaktor A enthält damit die Zahl der Teilchen, die gegen die Energiebarriere anlaufen sowie die Anlauffrequenz, d.h. A = N · n. Aber vielleicht auch, um ganz allgemein zu bleiben, noch andere, mit der Natur der Reaktion zusammenhängende konstante Parameter, die wir jetzt noch nicht kennen.
		Der Exponentialterm enthält eine ganz universelle Abhängigkeit von der Energie und der Temperatur. Er hat einen eigenen Namen und heißt Boltzmannfaktor.
	Wir betrachten nun einen Fall, in dem alle Teilchen zu Beginn des "Experiments" im Minimum bei E1 sitzen. Das System ist dann sicher nicht im Gleichgewicht. Was wird geschehen?
		Das sieht nun verlockend einfach aus: Alle Teilchen bei der höheren Energie E1 springen früher oder später über die Energiebarriere, irgendwann sind alle bei der kleineren Energie E2 und damit im Minimum der Energie.
		Fein. Aber Teilchen sind dumm, sie wissen nicht, dass sie "eigentlich" im Minimum bei E2 glücklich und zufrieden sein sollten, sondern tun was sie immer tun: Sie rennen gegen Energiebarrieren an - und zwar gegen alle Energiebarrieren, auch die in energetisch "falscher" Richtung.
	Unsere Sprungratengleichung gibt uns aber nicht nur die Sprungrate R1–2 von E1 nach E2, sondern auch die Sprungrate R2–1 von E2 nach E1.
		Das thermodynamischem Gleichgewicht das wir jetzt suchen, wird ein dynamisches Gleichgewicht sein müssen, bei dem keine Nettoreaktion mehr stattfindet. Insbesondere dürfen sich dann die Teilchenzahlen in den beiden Energieniveaus nicht mehr ändern.
		Das ist offenbar dann, und nur dann der Fall, wenn die beiden Sprungraten gleichgroß sind, weil dann genau so viele Teilchen in ein Energieniveau hinein- wie heraushüpfen. Der "Kontostand", d.h. die Teilchenzahl des Energieniveaus, ändert sich dann nicht mehr.
	Das läßt sich nun leicht als Gleichung hinschreiben.
		Die Wahrscheinlichkeit p1–2 eines Sprungs von E1 nach E2 ist durch den Boltzmannfaktor gegeben zu p1–2 = exp–(DE/kT), die Wahrscheinlichkeit p2–1 für einen Sprung zurück, von E2 nach E1, ist p2–1 = exp–[(E1 – E2 + DE)/kT].
		Denn die Höhe der Energiebarriere E2–1 im zweiten Fall ist nach obigem Bild offenbar
		E2–1  =  E1  –  E2  +  DE
	Die Gleichheit der Reaktionsraten erfordert nun
		R1–2 R2–1  = 1 =  A1–2 A2–1   ·   exp–[DE]/kT   exp–[E1 – E2 + DE]/kT  =  A1–2 A2–1  · exp E1 – E2 kT
		Die Energiebarriere DE fällt heraus, und da die Energiedifferenz E1 – E2 ein fester Parameter ist, macht die Gleichung eine Aussage über die notwendige Größe der Vorfaktoren A im Gleichgewicht.
	Die Vorfaktoren A1–2 und A2–1 sind nun im einfachsten Fall die Produkte der Teilchenzahlen N1 bei E1 bzw. N2 bei E2 mal der Anlauffrequenz n1, 2.
		Da n1 » n2 sein wird, erhalten wir eine Beziehung zwischen den Teilchenzahlen N1 und N2 im Gleichgewicht.
		Mit A1,2 = n · N1,2 erhalten wir eine der wichtigsten Gleichungen der Materialwissenschaft
		N1 N2   =  exp  –  E1 – E2 kT

	Das ist ein etwas überraschendes und ungeheuer wichtiges Ergebnis, da DE, die Höhe der Energiebarriere zwischen E1 und E2 gar nicht mehr vorkommt! Die Formel sagt im Klartext:
		Im thermodynamischen Gleichgewicht ist die Zahl an Teilchen N1 und N2, die zwei miteinander "korrespondierende" Energieniveaus E1 und E2 besetzen, nur durch den Boltzmannfaktor der Energiedifferenz E1 – E2 gegeben. (Vorzeichen immer so, daß bei der höheren Energie weniger Teilchen "sitzen").
		Das bedeutet, dass die Höhe der Energiebarriere DE zwischen den Niveaus für das Gleichgewicht belanglos ist. Eine hohe Barriere bedeutet nur, daß es länger dauert, bis die Gleichgewichtsverteilung erreicht ist.
		In anderen Worten: Der Weg ins Gleichgewicht; wie man da hin kommt und wie lange es ggf. dauert, ist für den Gleichgewichtszustand selbst egal.
	Dies ist nicht im Widerspruch zu obiger Aussage, daß ausschließlich die Höhe der Energiebarriere, in unserem Beispiel DE, für die Wahrscheinlichkeit des Übergangs entscheidend ist. Nochmals:
		Die Differenz der Energien entscheidet über die Besetzung, über die im zeitlichen Mittel konstanten Teilchenzahlen bei den Energieniveaus im Gleichgewicht.
		Die Höhe der Energiebarriere entscheidet über die Zeitdauer, die benötigt wird um Gleichgewicht zu erreichen.
	Die Erweiterung auf mehr als zwei Niveaus ist einfach. Obige Beziehung gilt für jede Kombination zweier Energieniveaus.
		Graphisch sieht das dann so aus:
		Auf jedem Energieniveau sitzen im Gleichgewicht gerade so viel Teilchen wie es der Boltzmannfaktor (bezogen auf die Energie des Grundniveaus) vorgibt.
		Gleichzeitig ist natürlich immer die Nebenbedingung zu erfüllen, dass SNi = N, d.h. dass die Summe der Teilchen auf allen Energieniveaus gleich der Gesamtzahl N sein muß.
		Falls das Grundniveau E0 deutlich tiefer liegt als das erste höhere Niveau E1 (Genauer: Falls E1 – E0 >> kT) dürfen wir in guter Näherung N0 » N setzen, d.h. wir haben nur wenige Teilchen auf höheren Niveaus.
		Dieser Fall ist die Regel, wir unterstellen ihn jetzt immer automatisch. (Falls wir das nicht tun, wird's etwas schwieriger; Neugierige können den Link betätigen
		Die nebenstehende Zeichnung zeigt das natürlich nicht, sonst wäre nichts mehr zu sehen!
	Wir kommen zum Schluß, daß unter Verwendung der Boltzmannformel für die Sprungwahrscheinlichkeiten, im thermodynamischen Gleichgewicht auch Zustände mit höheren Energien als die kleinstmögliche Energie des Systems mit einigen Teilchen besetzt sind.
		Das ist auch nicht verwunderlich, denn thermodynamisches Gleichgewicht erfordert die Minimierung der freien Enthalpie des Systems, nicht die Minimierung der Energie der einzelnen Teilchen.
		Wären alle Teilchen bei der tiefstmöglichen Energie (besser Enthalpie) des Systems, wäre die Entropie zu klein, denn es gibt nur eine Möglichkeit um alle (ununterscheidbaren) Teilchen energetisch anzuordnen.
	Aus dem Boltzmannfaktor läßt sich damit eine (für unserer Zwecke) simple Verteilungsformel für die Verteilung von Teilchen auf verschiedene Energiezustände angeben, die sogenannte Boltzmannverteilung:
		Sie sagt in Worten:
		Falls ein thermodynamisches System verschiedene angeregte Energiezustände Ei relativ zum Grundzustand E0 hat (mit E0 = Zustand mit der kleinsten Energie := 0), dann ist im thermodynamischen Gleichgewicht die Zahl der Teilchen Ni bei der Energie Ei (näherungsweise) gegeben durch Ni   =  N 0 · exp – Ei kT
		Man kann diese Formel gar nicht genug hervorheben; sie ist absolut zentral für nahezu alles, was auch nur entfernt mit Kinetik, mit Veränderungen zu tun hat.
		Im Gegensatz zur Schrödingergleichung (die sicher noch fundamentaler und wichtiger ist), werden wir diese Gleichung aber nicht nur gelegentlich, sondern sehr häufig benötigen.
		Dabei dürfen wir, wie schon ausgeführt, in guter Näherung N0 » N = Gesamtzahl der Teilchen setzen, falls Ni << N0 gilt.
	Das ist eine sehr weitreichende Aussage! Wir behaupten nicht mehr und nicht weniger, als daß die freie Enthalpie eines jeden Systems, in dem es für die (klassischen) Teilchen verschiedene erreichbare Energiezustände gibt, immer minimal ist, wenn die Teilchen nach der Boltzmannverteilung, oft auch Boltzmann Statistik genannt, die Energieniveaus besetzen.
		Cool! Heißt das, nie mehr Anordnungmöglichkeiten abzählen und mühsam mit Fakultäten hantieren zu müssen? Die Antwort ist: im Prinzip - Ja! Aber ein bißchen müssen wir später doch noch aufpassen. Wir haben zwei Einschränkungen einfach unter den Tisch fallen lassen, nämlich:
		1. Falls die Quantenmechanik zuschlägt und wir das Pauli-Prinzip beachten müssen, kann die Formel nicht stimmen: es können höchstens so viele Teilchen bei der gleichen Energie "sitzen", wie der Entartungsgrad dieser E-Niveaus angibt. Sonst würden wir das Pauli-Prinzip verletzen Und das ist absolut verboten!
		2. Vielleicht gibt es bei irgend einer Energie gar nicht so viele reale Plätze wie Teilchen, die darauf sitzen möchten. Dann muß man etwas tiefer nachdenken.
		In den meisten klassischen Systemen gibt es aber diese Einschränkungen nicht. Wir müssen tatsächlich nie mehr Kombinatorik treiben; dafür aber etwas abstrakter denken, wie wir sofort sehen werden.
		Wer jetzt schon recht abstrakt denken will, schaut sich den Link an, dort sind einige der obigen Näherungen nicht mehr gemacht
	Warum gilt diese einfache Verteilungsfunktion? Weil der Boltzmannfaktor oder die Boltzmannverteilung, die hier ohne Begründung postuliert wurden, unmittelbare Konsequenzen länglicher Rechnungen in der statistischen Thermodynamik sind.
		Eine Besetzung der Energieniveaus eines (klassischen) Systems mit (klassischen) Teilchen dergestalt, daß die freie Enthalpie ein Minimum hat, führt zwingend (ohne Näherungen!) auf die Boltzmannverteilung.
		Wir werden diese Thematik im 2. Teil des Hyperskripts vertiefen, und dann auch sehen, was sich ändert, wenn wir nicht klassische Teilchen, sondern quantenmechanische Teilchen betrachten.
	Nochmals: Die Boltzmannverteilung ist eine der wichtigsten Formeln der Materialwissenschaft. Wir werden ihr noch oft begegnen; im nächsten Unterkapitel werden wir sie benutzen um die Diffusion von Teilchen quantitativ zu beschreiben. Vorher wollen wir sie aber noch kurz auf die Gleichgewichtskonzentration atomarer Fehlstellen anwenden.

	Leerstellenkonzentration im Gleichgewicht
	Ausgerüstet mit dem Werkzeug der Boltzmannverteilung, hätten wir die Formel für die Leerstellenkonzentration, wie oben bemerkt, sofort hinschreiben können. Denn ein Atom auf einem Gitterplatz hat energetisch gesehen 2 mögliche Energiezustände:
		Es kann auf einem beliebigen Gitterplatz bei der Energie E0 "sitzen". Der "Platz" auf dem das Teilchen sitzt bezieht sich jetzt auf ein Energieniveau, nicht mehr auf eine Koordinate.
		Es kann einen beliebigen Gitterplatz frei geben, d.h. über irgendeinen Weg aus dem Kristall "verschwinden". Dann "besetzt" es energetisch das Niveau E0 + EV. (Wir schreiben jetzt EV statt HF(V) für die Bildungsenthalpie bzw. -energie).
	Diese Betrachtung zeigt, wie angemerkt, den notwendigen höheren Grad an Abstraktion; im wesentlichen daß wir über "Plätze" im Energieraum reden.
		Wer mit dem "Niveau" E0 + EV Probleme hat, soll sich einfach mal vorstellen, einem Atom kontinuierlich Energie zuzuführen. Nur falls man mindestens die Bildungsenergie der Leerstelle trifft, kann strukturell etwas passieren,. Wie es passiert, d.h. wie der Weg zum neuen Zustand aussieht, kann uns, wie oben ausgeführt, dabei egal sein sofern wir genügend lange warten können. Bei allen anderen Energien besetzen wir bloß die uns hier nicht interessierenden Energieniveaus der Schwingungen im Potentialtopf.
		Immer noch abstrakt? Nun gut - auch hier gilt der erste Hauptsatz der Betriebswirtschaftslehre!
	Mit der Boltzmannverteilung wird dann die Zahl der Atome bei E0 + EV = Zahl der Leerstellen
		NV  = N0 · exp –  EV kT
		d.h. wir erhalten sofort die alte Formel. Wenn das kein Fortschritt ist!
	Für Zwischengitteratome gilt selbstverständlich sinngemäß dasselbe.
		Hier läßt sich auch leicht einsehen, daß bei der Bildungsenergie der Zwischengitteratome, Ei, tatsächlich ein zweites energetisches Niveau für richtige Atome liegt, man muß nicht einmal sehr abstrakt denken.

© H. Föll (MaWi 1 Skript)