 |
Bei der Frage, mit wievielen unterscheidbaren Möglichkeiten
man mit einem digitalen Würfel (z.B eine Münze: Kopf = + 1, Zahl = – 1) und n
Würfen eine Zahl x zwischen +N und –N würfeln kann, ist es hilfreich,
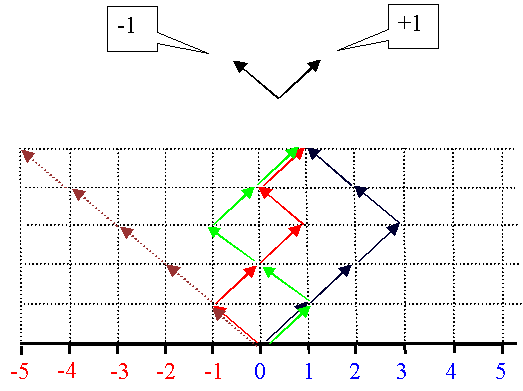
sich die Wege zum Ziel graphisch darzustellen. Ein Beispiel: |
|
|
|
|
 |
Viele Wege führen zum Ziel +1 (3 sind eingezeichnet), nur einer führt
zum Ziel –5. Die Wahrscheinlichkeit, eine bestimmte Zahl zu würfeln, ist natürlich direkt proportional
zur Zahl der Wege zum Ziel. |
 |
Nur Wege, die in diesem Diagramm unterscheidbar sind, sind unterscheidbare Anordnungen! |
| |
© H. Föll (MaWi 1 Skript)
![]() Ableitung der Gauss Verteilung
Ableitung der Gauss Verteilung