|
Wir suchen eine Beziehung, die den Diffusionstrom j des 1. Fickschen Gesetzes mit den individuellen Sprüngen von irgendwelchen Teilchen koppelt.
|
|
 |
Dabei beschränken wir uns der Einfachheit halber auf Materialien mit bekannten
(und einfachen) Mechanismen der atomaren Diffusion - in anderen Worten, wir behandeln Sprünge von Leerstellen oder
Zwischengitteratomen in einfachen Kristallen wie in Kapitel 6.2.1 behandelt. |
|
 |
Wir behandeln das Problem außerdem in einer eindimensionalen
Geometrie, denn wir sind nur am Prinzip interessiert. |
|
 |
Die Erweiterung auf drei Dimensionen, komplizierte Kristalle, exotische atomare Mechanismen
usw., obwohl nicht unbedingt trivial, bringt keine wirklich grundlegenden neuen Einsichten und wird hier nur kursorisch
gestreift. |
 |
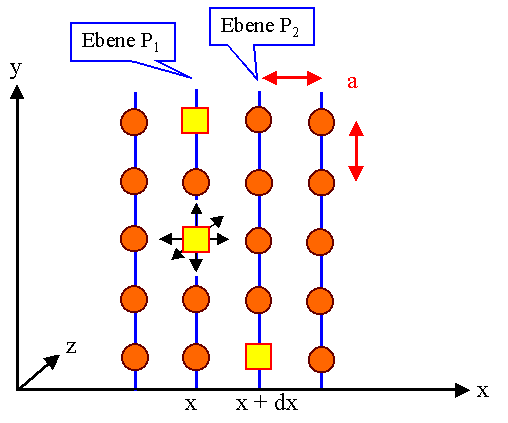
Betrachten wir nun zwei Netzebenen
eines einfachen Kristalls, die senkrecht zur betrachteten Diffusionsrichtung stehen
und diffusionsfähige Teilchen enthalten - im Beispiel sind das (sehr viele) Leerstellen: |
| |
|
 |
Wir interessieren uns nur für den (Netto) Fluß der Leerstellen in x
- Richung, den Diffusionsstrom der Leerstellen. Der Fluß von Atomen,
die über einen Leerstellenmechanismus diffundieren, wäre dann entgegengesetzt gleichgroß. |
|
 |
Wir unterstellen kein Gleichgewicht, sondern
eine vom Ort abhängige Leerstellenkonzentration cV(x,y,z). Da wir das Problem eindimensional
betrachten, nehmen wir nur eine Abhängigkeit der Lerstellenkonzentation von der x - Richtung an, cV(x,y,z)
= cV(x). |
|
 |
Wir haben auf jeder der betrachteten Ebenen eine bestimmte Zahl
an Leerstellen pro Einheitsfläche oder Flächenkonzentration
cF(x) (Einheit damit cm–2), die über die lokale Volumenkonzentration
cV(x) berechenbar ist. |
|
 |
Die Beziehung dazu ist einfach, wir müssen nur die Volumenkonzentration cV
mit a zu multiplizieren, um aus der Volumendichte eine Flächendichte
bzw. Zahl pro Einheitsfläche zu machen.. |
|
 |
Wer das nicht unmittelbar einsieht oder zumindest nach kurzem Nachdenken verifizieren kann,
sollte unbedingt obigen Link betätigen! |
 |
Wir bezeichnen jetzt die Flächendichte
aus Gründen der Schreibökonomie direkt mit dem Index der Ebene; d.h. P1 ist die Flächendichte
der Leerstellen auf der P1-Ebene, usw.. Wir haben dann |
| |
| P1 = |
a · cV(x) |
| |
| P2 = |
a · cV(x + dx) |
|
|
 |
Nun kommt ein essentieller Trick: Wir setzen dx = a = Gitterkonstante
für die betrachtete kubisch-primitive Geometrie, weil kleinere differentielle dx keinen physikalischen
Sinn mehr ergeben, und erhalten |
|
|
|
 |
Als nächstes betrachten wir die Sprungraten in x - Richtung,
d.h. denjenigen Anteil der Sprünge der Leerstellen auf einer der betrachteten Ebenen, der in x - Richtung
erfolgt. |
|
 |
Wir definieren
- r1-2 = Sprungrate in x - Richtung von P1 nach P2
- r2-1 = Sprungrate in –x - Richtung von P2 nach P1
und erhalten für unsere simple kubische Geometrie |
| |
| r1-2(T) = r2-1(T) = |
1
6 | · r(T) |
|
|
|
 |
Die Sprungrate in x- oder –x -Richtung der Leerstellen irgendeiner
Ebene ist nämlich 1/6 der Gesamtzahl der Sprünge r(T). Denn von den sechs
geometrisch möglichen Spüngen führt nur einer in die +x-
bzw. –x -Richtung. Die Sprungrate selbst ist, wie wir
wissen, in einem gegebenen Material nur eine Funktion der Temperatur T. |
 |
Damit erhalten wir für die Zahl der Teilchen, die pro Sekunde und cm2
von P1 nach P2 springen, d.h. für den rechtsgerichteten
Anteil des Diffusionstrom j1-2 (und das ist nicht der Nettodiffusionsstrom des 1. Fickschen Gesetzes!), |
| |
|
|
 |
Das ist, wenn man so will, der Strom an Leerstellen, der aus der Ebene P1
in x - Richtung hinausfließt. Dieser Strom wird teilweise kompensiert
durch den Stromanteil j2-1, der von P2 nach P1
zurückfließt. Dieser Stromanteil ist gegeben durch . |
| |
|
|
 |
Mit den obigen Beziehungen erhält man für die beiden Teilströme . |
| |
| j1-2 = |
r · a · c(x)
6 |
|
| |
|
| j2-1 = |
r · a · c(x + a)
6 |
|
|
 |
Der Nettostrom
jx in x - Richtung nach dem 1. Fickschen Gesetz ist nun genau die Differenz der beiden Teilströme, wir erhalten
|
| |
| jx = – |
a · r
6 |
· |
æ
è |
c(x + a) – c(x) |
ö
ø |
|
|
|
 |
Erweitern wir mit a/dx (und berücksichtigenm dass dx =
a gesetzt wurde) erhalten wir für eine Dimension |
| |
| jx = – |
a2 · r
6 |
· |
c(x + a) – c(x)
dx | = – |
a2 · r
6 |
· |
dc(x)
dx |
|
|
|
 |
Wir müssen nur noch den Vorfaktor
vor der Ableitung mit dem Diffusionskoeffizienten
D gleichsetzen , d.h. wir definieren jetzt |
| |
|
|
 |
und wir haben unmittelbar das 1. Ficksche
Gesetz |
| |
| jx = – |
a2 · r
6 |
· |
dc(x)
dx |
= – |
D · |
dc(x)
dx |
|
|
 |
Das 1. Ficksche Gesetz kann also für den eindimensionalen Fall der
Diffusion in kubisch primitiven Kristallen in einfacher Weise physikalisch sauber hergeleitet werden (Mathematiker hätten
allerdings etwas Bauchweh bei der verwendeten Identität dx = a). |
|
 |
Gleichzeitig erhalten wir (für das kubisch primitive Gitter) einen Ausdruck
für den phänomenologischen Diffusionskoeffizienten D, der ausschließlich
die atomaren Größen Gitterkonstante und
Sprungrate enthält. |
 |
Die Erweiterung auf (fast) beliebige Kristalle ist nun schnell pauschal zu vollziehen. |
|
 |
Die einzige Größe, die Gittereigenschaften widerspiegelt, ist der Faktor 1/6
und die Sprungdistanz, die nicht immer = a sein muß, sondern allgemein, für den Sprungtyp i,
Dxi sein kann. Der Index i numeriert, auf das obige Beispiel
bezogen, die 6 geometrisch verschiedenen Sprünge und berücksichtigt, daß in komplizierteren Gittern,
die x- Komponente des Sprungs von i abhängen kann. |
|
 |
Der Diffusionskoeffizient ist dann gegeben durch |
| |
|
|
 |
wobei g eine gitterspezifische Konstante,
der sogenannte Geometriefaktor ist, und D(T) die Temperaturabhängigkeit
der Sprungrate hat. |
 |
Der Geometriefaktor g
eines Gitters ist dabei wie folgt definiert: |
|
|
| g = ½ ·
|
S
i |
æ
è |
Dxi
a | ö
ø
| 2 |
|
|
|
 |
Der Faktor 1/2 berücksichtigt, daß in der Summierung über alle möglichen
Sprünge nur die Hälfte genommen werden darf, da die andere Hälfte dem Rücksprung entspricht; der Ausdruck
Dxi/a berücksichtigt nur die x-Komponente
eines Sprungs in Bruchteilen der Gitterkonstante a des betrachteten Gitters. |
|
 |
Für einfache Gitter ist g leicht berechenbar und für das fcc
und bcc Gitter netterweise = 1; wir machen dazu gleich eine Übung. |
 |
Die Erweiterung auf drei Dimensionen ist damit auch schnell vollzogen.
|
|
 |
In isotropen Kristallen (das sind neben den kubischen
Kristallen auch alle Polykristalle mit statistischer Orientierung der Körner), ist keine
Richtung ausgezeichnet; die Gleichung für die x Komponente gilt auch für die y- und
z- Komponente des Diffusionstroms. Mit der bekannten Gleichung für
die Sprungrate erhalten wir die verallgemeinerte Vektorgleichung des 1. Fickschen
Gesetzes: |
| |
| j(r,T) = |
– D0 · exp – |
EM
kT |
· 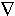 c(x,y,z) c(x,y,z) |
|
|
|
 |
In dem Vorfaktor D0 steckt jetzt alles was nicht so ganz spannend
oder gut bekannt ist: Die Anlauffrequenz(en), der Geometriefaktor, die Gitterkonstante(n), und vielleicht noch (unwichtige)
Terme, die wir hier gar nicht betrachtet haben. |
 |
In anisotropen Kristallen wird es komplizierter.
Dann muß jede Richtung getrennt betrachtet werden, aus dem skalaren Diffusionskoeffizient wird ein Tensor.
Damit wollen wir uns aber hier nicht weiter befassen. |
|
|
|
 |
Es bleibt noch eine Frage offen, die Frage die wirklich von Einstein (und Smoluchowski)
zuerst gestellt und beantwortet wurde (die obige Ableitung folgt indirekt daraus). |
|
 |
Wenn ein Teilchen bei jedem
Sprung eine fixe Distanz zurücklegt und jede möglich Richtung eines Sprungs
gleich wahrscheinlich ist (d. h. die Sprünge sind rein statistisch), wie weit kommt
es dann im Mittel nach N Sprüngen? |
|
 |
Oder, gegeben die Sprungrate r, wie weit kommt es im Mittel nach t
Sekunden (entsprechend r · t Sprüngen)? |
|
 |
Eine einfache Frage, mit einer sehr einfachen Antwort, und einer sehr schwierigen Herleitung! |
 |
Dieses Thema wollen wir im nächsten Unterkapitel näher betrachten. |
© H. Föll (MaWi 1 Skript)