 |
Wir brauchen eine Notation, die uns erlaubt, bestimmte Richtungen
und Ebenen in einem beliebigen Gitter eindeutig anzusprechen, d.h. eine mathematische
Formulierungen für Aussagen wie "entlang der Flächendiagonalen" oder "auf der Würfelebene". |
|
 |
Man könnte mehrere Arten von Rezepten angeben, mit denen man eine Richtung
(d.h. einen Vektor) oder eine Ebene in einem Gitter eindeutig indizieren kann. Es gibt aber ein besonderes System, die sogenannten
Miller
Indizes, die zwar vielleicht nicht sofort einleuchten, mit denen man aber (später)
sehr bequem rechnen kann. |
|
 |
Wir betrachten zunächst die Miller Indizierung
für Richtungen: |
| |
| Definition (und Rezept) |
Eine Richtung in einem Gitter wird durch drei ganze Zahlen indiziert, indem
|
- Der Ursprung der EZ auf die gewünschte Richtung gelegt wird,
- Ein Vektor in der gewünschten Richtung in kleinstmöglichen ganzzahligen Komponenten der Basisvektoren ausgedrückt
wird
- Auftauchende negative Zahlen durch einen Überstrich darstellt werden (in html nicht leicht
darstellbar, wir schreiben stattdessen mit dem Minus ("–") oder Strich (" ' ") Zeichen)
und
- Das erhaltene Zahlentripel uvw in eckige
Klammern [uvw] gesetzt wird wenn es sich um eine spezifische Richtung handelt,
und in spitze Klammern <uvw>, wenn die Gesamtheit
aller kristallographisch gleichwertigen Richtungen gemeint ist.
|
|
 |
In dem unten gezeigten zweidimensionalen Gitter erhalten die Richtungen 1
- 5 damit folgende Miller Indizierung |
| |
| |
| | | | |
| | Richtung 1 | | [1, –1]
| = | [1 1'] | | |
| | | |
| Richtung 2 | | [1, –1/3] | = |
[3 1'] | | | |
| | | | Richtung 4 |
| [–1, 1] | = | [1' 1] |
| | | | |
| | Richtung 5 | | [1, 0] |
| | | | | |
| | | Richtung 6 | |
[–1, –1] | = | [1' 1'] |
| | | | | |
|
|
|
 |
Ausgesprochen wird z.B. die <110>-Richtung nicht als "einhundertzehn
Richtung", sondern als "eins, eins, null Richtung" oder noch genauer
als: "eins, eins, null Richtungstyp". |
 |
Man kann das Zahlentripel <uvw> in einer der spezifichen Ausprägungen
z.B. [uv'w] natürlich auch als Vektor auffassen, der in die gewünschte Richtung zeigt. Wir haben dann einen
simplen Translationsvektor des Gitters, dessen Betrag allerdigs
keine relevante Information enthält (die haben wir durch das Kürzen auf kleinstmögliche Zahlen "beseitigt").
Bei Ebenen wird das aber anders sein. |
 |
Was kristallographisch gleichwertig ist, hängt vom Gittertyp ab! |
|
 |
Im kubischen Gitter sind alle möglichen Permutationen (inkl. Negation) der Indizes immer
gleichwertig; aber schon im hexagonalen Gitter gilt das nicht mehr. |
|
 |
Andererseits sind gerade im hexagonalen Gitter
Richtungen kristallographisch gleichwertig, die verschiedene Miller-Indizes haben. Die in der Basisebene liegenden Richtungen,
die zu den Ecken des gleichseitigen Sechseckes zeigen, das die Basisebene definiert, haben Indizes wie z.B. [110],
[100], [010], d.h. die Miller Indizes sind nicht Permutationen einer allgemeinen
Richtung wie z.B. <100>. Für Ebenen (siehe unten) ist es ähnlich. |
|  |
Wer das nicht versteht, hat die Übungsaufgabe
nicht gemacht! Das sollte man her unbedingt tun, und sei es nur, dass man sich Aufgabe und Lösung anschaut.
|
 |
Man hat deshalb für das hexagonale Gitter (das in der Praxis sehr wichtig ist), eine eigene
Abart der Miller-Indizes erfunden, die auch in diesem Fall die vorhandenen Symmetrien direkt aufzeigt: Man nimmt einfach
zu den Basisvektoren a1, a2 und c noch einen
weiteren (an sich unnötigen) "Basisvektor" dazu, der als a3 = – (a1
+ a2) definiert wird (damit ist a3 mathematisch gesehen natürlich
kein Basisvektor, da nicht linear unabhängig!), und indiziert dann mit 4 Indizes.
|
|
 |
Aus den oben aufgezählten Richtungen wird dann [1,1,2',0], [2,1',1',0], [1',2,1',0];
die Symmetrie in den Indizes wird sichtbar. |
|
 |
Wir wollen uns damit aber nicht weiter befassen (außer, dass wir noch eine Übung machen); alles
Wissenswerte zur Vierer-Indizierung bei hexagonalen Gittern findet sich im Link |
| |
|
| | |
|
|
Mathematische Beschreibung von Ebenen im
Gitter |
| |
|
 |
Wir brauchen jetzt eine Notation, die uns erlaubt bestimmte Ebenen in einem beliebigen Gitter eindeutig anzusprechen, zum Beispiel die "Würfelseite"
bei einem kubischen Gitter, oder die "Basisebene" bei einem hexagonalen Gitter. |
|  |
Man könnte sich zunächst denken, daß man dafür das Zahlentripel nehmen
könnte (evtl. auf kleinste ganze Zahlen reduziert), das sich aus den Schnittpunkten einer Ebene mit den Basisvektoren
des Gitters ergibt - wie bei den Richtungen |
|
 |
Könnte man auch, aber es gibt nicht immer einen Schnittpunkt. Die Würfelseite eines
kubischen Gitters schneidet immer nur einen der Basisvektoren; zu den anderen liegt sie parallel (bzw. enthält sie). |
 |
Deshalb, aber auch aufgrund anderer Vorzüge die wir noch kennenlernen werden, wählt
man eine zunächst etwas umständlich erscheinende Definition: |
|
|
| Definition (und Rezept) |
Eine Ebene in einem Gitter wird durch drei ganze Zahlen indiziert, indem man
|
- Den Ursprung der EZ
nicht in die zu indizierende Ebene legt, sondern in eine Nachbarebene.
- Die Schnittpunkte der Ebene mit den Basisvektoren bestimmt (wenn kein Schnittpunkt
vorhanden ist, entspricht das "¥").
- Das erhaltene Zahlentripel reziprok darstellt, und die resultierenden
Brüche durch Erweitern ganzzahlig macht; aus ¥ wird dadurch 0. Nicht erlaubt ist Kürzen, falls die reziproken Zahlen keine Brüche sind (Aus den Schnittpunkten
1/2, 1/2, 1/2 erhält man 2, 2, 2 und nicht 1, 1, 1).
- Auftauchende negative Zahlen durch einen Überstrich darstellt (in
html nicht darstellbar, wir schreiben stattdessen mit '- Zeichen)
- Das Zahlentripel hkl in runde Klammern (hkl) setzt, falls es sich um eine spezifische
Ebene handelt, und in geschweifte
Klammern {hkl}, falls die Gesamtheit aller kristallographisch gleichwertigen Ebenen
mit denselben Indizes gemeint ist.
|
|
 |
Dazu drei Beispiele, die absichtlich etwas unklar gezeichnet sind, um nicht sofort falsche
Assoziationen hervorzurufen. |
|
 |
Insbesondere ist es wichtig sich klarzumachen, daß mathematische
Ebenen in einem mathematischen Gitter ¥ ausgedehnt sind. Die Begrenzungslinien sind
also immer nur zeichentechnisch bedingt. |
| |
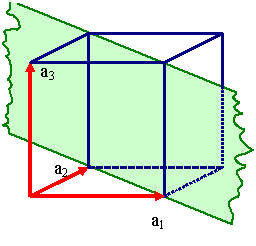 |
Kubisches Gitter
Schnittpunkte bei
1, 1, ¥
Indizes (110) |
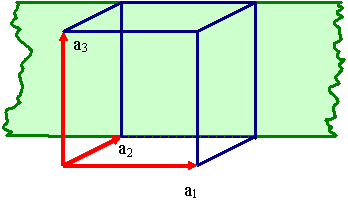 |
Kubisches Gitter
Schnittpunkte bei
¥, 1, ¥
Indizes (010) |
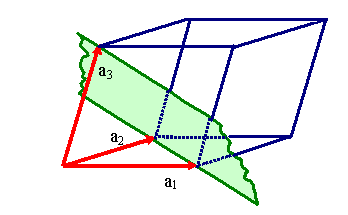 |
Triklines Gitter
Schnittpunkte bei
1, 1, 1
Indizes (111) |
|
 |
Wichtig ist: Alle Ebenen
die man in gleicher Weise in eine EZ einzeichnet, haben die gleiche Indizierung. |
|
 |
Das Kürzel (112) bezeichnet also nicht eine
Ebene, sondern einen Satz von ¥ viele parallel laufende Ebenen; {112} entsprechend
mehrere Sätze ¥ vieler, ¥ ausgedehnter,
parallel laufender Ebenen. |
|
 |
Das Kürzel (hkl) kann man aber auch als die Komponenten eines
Vektors auffassen, der dann per Definitionem senkrecht auf der Ebene steht, die er charakterisiert. Der Betrag dieses Vektors
- nennen wir ihn mal reziproken Gittervektor - hat denn eine wichtige Bedeutung;
wie wir weiter unten noch lernen werden. |
 |
Eigentlich ist damit alles gesagt; vielleicht ist noch der Hinweis hilfreich,
daß man bei hexagonalen Gittern natürlich auch bei den Ebenen eine Vierer-Indizierung wie bei den Richtungen einführt. |
 |
Erfahrungsgemäß wird der Anfänger (und nicht selten auch der Experte)
beim Arbeiten mit den Miller Indizes von Ebenen aber Probleme haben und Fehler machen. Deshalb hier noch einige Bemerkungen. |
 |
Eine gewisse Konfusion kann entstehen, weil es in der Kristallographie eigentlich
zwei Konzepte von Ebenen gibt: |
|
 |
- Die mathematische Definition von oben, bezogen auf mathematische
Ebenen im mathematischen Gitter.
- Die gegenständliche Definition, in der Kristalle
als Stapelfolgen von einer Ebene zugeordneten Atomen oder Atomgruppen betrachtet werden.
|
|
 |
Man redet im ersteren Falle auch von Netzebenen, im letzteren
Fall von Kristallebenen. Die {111} - Kristallebene
in einem Diamantgitter enthält dann beide Atome der Basis; mindesten eines davon
liegt dabei nicht auf der Netzebene. Das ist ein wichtiger Unterschied, den man sich
klarmachen sollte; hier ein Bild dazu für die Diamantstruktur. |
|
|
|
|
 |
Die gelb gezeichnete {100} Kristallebene enthält den ganzen Satz von Atomen, die
schattiert gezeichnet sind. Aufeinanderstapeln solcher Kristallebenen produziert den Kristall. |
 |
Ähnlich ist es, wenn man eine mathematisch definierte Ebene in einen Kristall,
und nicht in ein Gitter einzeichnen will. Im Si-Kristall kann man beispielsweise
eine {100} Ebene auf zwei Weisen durch Atome
legen (oben z.B durch die blauen oder roten Atome); sie erscheint damit als nicht eindeutig definiert. |
|  |
Hat man obige Punkte nicht ganz sauber verstanden, wird man leicht falsche Zahlen generieren,
wenn man z.B. die Zahl von Atomen pro cm2 auf einer Ebenen ausrechnet, denn jetzt muß man die Ebene
im Gitter mit dem Kristall, d.h. auch mit der Basis kombinieren. |
 |
Triviale, aber immer wieder gerne gemachte Fehler sind: |
|  |
1. Als allgemeine Ebene nur eine Ebene zu sehen
und nicht die Gesamtheit aller äquivalenten Ebenen - die Ebenenschar |
|
 |
2. Zu glauben, daß z.B. die {200} Ebenen nur die Ebenen sind, die zwischen den {100} Ebenen stecken. Hier kommt obige Bemerkung
zum Tragen, daß nicht gekürzt werden darf. Die {200}-Ebenen sind etwas
anderes als die {100}-Ebenen! Das ist hier illustriert: |
|
|
|
|
 |
3. Man hat immer die Tendenz, Beziehungen, Regeln und Vorstellungen, die von kubischen Gittern geprägt worden sind, kritiklos auf nichtkubische
Systeme zu übertragen. Das kann sehr falsch werden! Zum Beispiel sind in nichtkubischen
Kristallen nicht alle Ebenen zu den möglichen Indizespermutationen kristallographisch gleichwertig. Für Richtungen
im hexagonalem Gitter haben wir das schon gesehen (siehe das hexagonal Gitter von oben);
für Ebenen ist es nicht anders. |
|
 |
4. Nochmals: Vorsicht ist auch geboten, selbst bei kubischen Kristallen, wenn man nicht
die mathematische Netzebene, sondern die mit Atomen belegte
Kristallebene betrachtet. Wenn man die (111) Ebene oder die (1'1'1') Ebene in z.B. GaAs oder SiC
betrachtet, sieht man einen großen Unterschied: Auf der einen Ebene sitzen Ga- oder Si- Atome, auf der
anderen As- bzw. C-Atome. Dies sieht nicht nur anders aus, sondern führt oft zu dramatischen Unterschieden
der Eigenschaften. Bei der Züchtung von SiC Kristallen erhält man völlig verschiedene Strukturen,
wenn man einen Kristall auf der (111)- oder (1'1'1')-Ebene eines Keimlings wachsen läßt (vereinfacht
gesagt wird das SiC in einem Fall kubisch, im anderen hexagonal - bei immer kubischem Keimling!). |
 |
Offensichtlich muß hier geübt werden! |
|
|
|
|
Rechnen mit Miller Indizes |
| |
|
 |
Wir können bereits einige Vorteile (aber noch längst nicht alle) der
auf den ersten Blick etwas seltsamen Miller Indizes ableiten und verwenden. Im folgenden sind sie für kubische
Gitter nur postuliert und aufgelistet; die Ableitungen und Beweise sind in
die Übung 3.2-3 verlegt. |
|
 |
1.
Kristallographisch äquivalente Richtungen und Ebenen haben immer den gleichen Satz
an Miller Indizes. |
|
 |
2. Die Richtung [hkl] steht immer senkrecht auf der Ebene (hkl). |
|
 |
3. Die Abstände dhkl zwischen zwei benachbarten
Ebenen sind direkt aus den Indizes berechenbar. Die Formeln für nichtkubische
Gittersysteme können etwas kompliziert sein, aber im kubischen Gittersystem gilt ganz einfach:
|
| |
| dhkl = |
a
(h2 + k2 + l2)1/2 |
|
|
|
 |
Im Zähler steht offensichtlich der Betrag des weite oben kurz angesprochenen reziproken Gittervektors mit den Komponenten (hkl)! Damit ist auch
schon hinreichend klar, warum die gewählte "reziproke" Definition der Miller Indizes für Ebenen sehr
vorteilhaft ist. |
 |
In der "Einführung in die Materialwissenschaft II" werden wir sehen, daß
die Miller Indizes noch weiterführen. Zum Beispiel treten sie direkt in den Formeln auf, die die Beugung von Wellen,
z.B. Röntgenstrahlen, in Kristallen beschreiben. |
|
 |
Aber zunächst wollen wir die obigen Beziehungen einüben |
| |
| Übung
3.2-3 |
| Beziehungen und Rechnungen mit Miller Indices |
|
| |
|
© H. Föll (MaWi 1 Skript)