 |
Ein Kristall hat eine regelmäßige (dreidimensionale - periodische)
Struktur. | |
Kristall = Gitter + Basis
|
|
|
 |
Ein Kristall besteht immer aus (mathematischem Punkt-) Gitter
und (physikalischer) Basis | |
| |
| |
|
|
 |
Das Punktgitter ist vollständig durch einen Satz dreier Vektoren ai
beschrieben; jedem Gitterpunkt kann ein Translationsvektor
T zugeordnet werden | |
| T | = |
u · a1 + v · a2 + w · a3
|
|
|
|
 |
Die Basis ist i.a. ein Atom oder ein Molekül, dabei sind der Komplexität keine Grenzen
gesetzt. | |
|
| |
| |
 |
Ein Gitter kann noch verschiedene Grade an Symmetrie
aufweisen: Neben der immer vorhandenenTranslationssymmetrie auch Rotations-, Spiegel- und Inversionssymmetrien. |
|
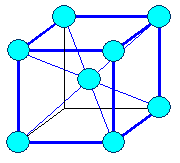
kubisch-raumzentriert
bcc |
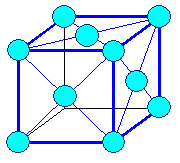
kubisch-flächenzentriert
fcc |
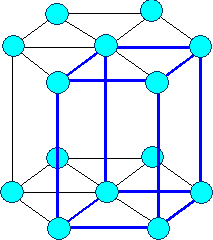
Hexagonal
hex |
|
|
 |
Je nach dem "Grad" der Symmetrie kann man genau 14 verschiedene "Bravais"-Gitter
unterscheiden. | |
|
 |
Drei davon sind besonders wichtig: fcc, bcc, und hcp. |
|
 |
Die Längen der Basisvektoren der Bravaisgitter heißen die Gitterkonstanten des Gitters. | |
| |
|
© H. Föll (MaWi 1 Skript)


