Ebenenabstand in nichtkubischen Gittersystemen

	Die Abstände zwischen benachbarten Ebenen mit denselben Miller-Indices berechnen sich wie folgt:
		Name des Kristallsystems Länge der Basisvektoren Zugehöriges unzentriertes Bravaisgitter (gelegentlich nur "sichtbare" Gitterpunkte eingezeichnet) Achsenwinkel Abstand zweier Ebenen mit Miller-Indices (hkl) Kubisch a1 = a2 = a3 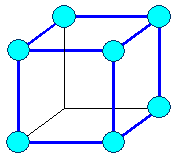kubisch-primitiv a = b = g = 900 dhkl  =  a (h2 + k2 + l2)1/2 Tetragonal a1 = a2 ¹ a3 a3 = c 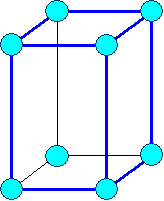Tetragonal-primitiv  a = b = g = 900 dhkl  =  a (h2 + k2 + a2/c2 · l2)1/2   Hexagonal a1 = a2 ¹ a3 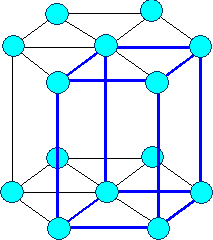Hexagonal (EZ ergänzt um hex. Symmetrie zu zeigen)  a = b = 900, g = 1200 dhkl  =  a {4/3(h2 + hk + k2) + a2/c2 · l2}1/2 Rhomboedrisch a1 = a2 = a3 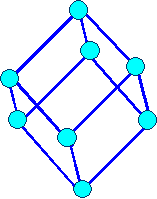Rhomboedrisch a = b = g ¹ 900 1 d2  =  (h2 + l2 + k2)sin2a + 2(hk + kl + hl)(cos2a - cosa) a2(1 - 3cos2a + 2cos3a) Orthorhombisch a1 ¹ a2 ¹ a3 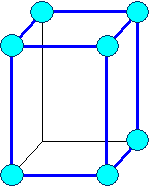Orthorhombisch-primitiv a = b = g ¹ 900 dhkl  =  1 {(h/a)2 + (k/b)2 + (l/c)2}1/2 Monoklin a1 ¹ a2 ¹ a3 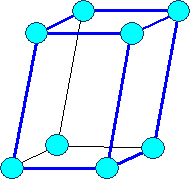Monoklin-primitiv a = b = 900, g ¹ 900 1 d2  =  h2 a2sin2b  +  k2b2  +  l2 c2sin2b  –  2hlcosb acsin2b Triklin a1 ¹ a2 ¹ a3 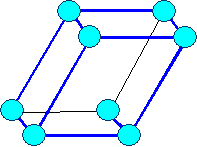a ¹ b ¹ g ¹ 900 Volumen EZ V  =  abc · (1 – cos2a – cos2b – cos2g           + 2cosa · cosb · cosg)1/2 Parameter S11 = b2c2sin2a S22 = a2c2sin2b S33 = a2b2sin2g S12 = abc2 (cosa · cosb – cosg) S23 = a2bc (cosb · cosg – cosa) S13 = ab2c (cosg · cosa – cosb) Abstand 1 d2  =  1 V2 · (S11h2 + S22k2 + S33l2          + 2S12hk + 2S23kl + 2S13hl)

Mit Frame

3.2.1 Richtungen und Ebenen im Gitter

Übung 3-4

Lösung Übung 3.2-3

© H. Föll (MaWi 1 Skript)